2.1 Одноместные предикаты, определение события

Обозначается Р(х), но х – имеет двузначную область определения {высокий, низкий}

х{H,L}

х{включено, выключено}

х{если, нет} и т.п.

Пример:

х – контакт

Р(х) - состояние контакта

Р(х) = {х замкнут} – утверждение (его истинность от х)

Электронная схема:

интерпретирует этот предикат

Р(х) = {х - замкнут} – True

P(x) = {х - разомкнут} – False

Р(х) = {х - сигнал} __ - есть сигнал; ----- - нет

интерпретация: детектор

Во всех случаях значения предиката с использованием двоичного кодирования отождествляется с значением переменной, т.о. переменная заменяет символ предиката Р(х) ~ х

Логические связки &, ,  применяется к событиям и позволяет формулировать составные утверждения в виде формул с предикатами. Связки имеют тот же смысл, что и в логике высказывания.

Пример: работа инкрементного датчика

Ф1

/Ф1

Ф2(,H,L)

\Ф2

Ф1 { -положительный фронт; -отрицательный фронт }

Ф2{H,L} влево  Ф1&Ф2 и вправо: Ф1 & Ф2 условие формулы

Во всех случаях формула с предикатами является булевой функцией и интерпретация сводится к вычислению булевой функций.

Алгоритм логического управления записывается в виде формул с событиями.

Обычно всегда формула содержит импликацию:

А(х₁, . . ., х_n)  В(у) где (х₁, . . ., х_n) – употребляются только связки &, , ,  используется вместо  (для удобства рассуждений)

Предикат В(у) – одномерный исполняемый предикат с двухзначной областью определения.

В(у) ~ у {включить, выключить}

{+1, -1}

Пример: в инкрементном датчике включается координата

S – текущее положение, путевая координата

S+:Ф₁ & Ф₂ или то же S-:Ф₁ & Ф₂

 

+1 -1

Пример управления прессом.

Задача: Включить двигатель (Д), если S₁,S₂,S₃ – выключены и х – замкнуты или у – разомкнут и плунжер двигается вниз.

Запись утверждена:

Д=S₁,S₂,S₃ & (х  y&П) – формальное описание алгоритма позволяет выбрать

интерпретацию:

а) аппаратная интерпретация (схема)

б) программная

а) б) МСS51(на ассемблере)

S1 1 &программа:

S2 mov C,S S₁  C

S3 orl C,S S₂  C  C

orl C,S S₃  C  C

1 Д mov R,C C  R

mov C,П П  C

y& anl C,y C & y  C

П anl C,x x  C

anl C,R S & R  C

mov Д,C C  Д

2.2 Одномерные предикаты определяющие свойства.

Р(х) = (хS), х – целые числа

Предикат тождественно истинный, если выполним на всех интервалах, предикат тождественно ложный, если не выполним на всех интерпретациях, предикат выполнимый, если выполняется хотя бы на одной интерпретаций.

Для таких предметов применима теоретико-множественная интерпретация.

W – предметная область, универсум

q(x) – предикат называется характеристической функцией подмножества Q  W (Q – подмножество значений, где предикат q(x) – истинный)

Q – называется эксистенцыал

Составные утверждения с предикатами формируются с применением логических связок (&, , ). Формулы имеют теоретико-множественную интерпретацию, называется диаграммами (в частности, Эйлера-Венна).

(которой приписана характеристическая функция)

Определение: Предикат r(х) выполним на всех интерпретациях, где r(х) – ложный т.е. не выполним.

r(х) = (х1) 

 r(х) =  (х1) = (х1)

Определение (коньюнкции): r(x) & q(x)

Пример: Пусть Р(х) = (х делится на 2)

q(х) = (х делится на 5)

Р(х) & q(x) – это формула, область истинности которая совпадает с утверждением «х делится на 10»

Определение: (дизъюнкция)r(x)  q(x)

RQ

x[0,5 20]

((x  0,5)(x=0,5)) & (x 20))

(p(x)  q(x)) & r(x) пример формулы с предикатом

Правила де Моргана:

 (р(x) & r(x)) =  p(x)   r(x)

на диаграммах



 р(x)   r(x)  (P  Q)

Определение: (импликация): r(x)  p(x) 

 (r(x)  p(x))  r(x) – истинно

q(x) – ложно т.е. r(x) &  p(x)



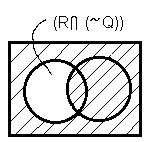
r(x)  p(x) тождественно истинная импликация

изображение экстенсионалов

R c P

 соотношение между экстенсионалами

Если известны экстенсионалы, то для конечных или бесконечных множеств можно построить экстенсионал формулы с предикатами.

Диаграмма строится для формул, состоящих из не более трех предикатов.

Диаграммы можно использовать для иллюстрации законов для бесконечных множеств.

Формулы с кванторами для одноместных предикатов.

Определение: формула с квантором всеобщности (x)Р(х) истина, если на всех значениях на области интерпретации хW:

(x) «для всякого хW» - квантор всеобщности Р(х) – истинно.

Квантор всеобщности – есть обобщение связки конъюнкции на всю область интерпретации, т.е. (x)Р(х) = Р(e₁)&Р(e₂)& . . . &Р(e_n); _iW

Если W-конечно, то тогда квантор – это просто конъюнкция высказывании (составное).

Если W-бесконечно, то (x) – совершенно новая связка. (x)Р(х) – высказывание, кот может быть истинным или ложным (оно не имеет теоретико-множественной интерпретации и является просто точкой).

Тождественно-истинное высказывание:

(x)Р(х) = (х + х = 2х) = Т, хD - истинно

(x)Р(х) = (2х = 5) = F, хD – F – ложно

Определение:

Формула с квантором существования (x)Р(х): «существует х из W, где Р(х) – истина».

Истинно, если по крайней мере на одном наборе аргументов х – предикат истина.

Квантор существования – обобщение дизъюнкции. Если W – конечная, то (x)Р(х) = Р(e₁)  Р(e₂)  . . . Р(e_n); {Т,F} ; Р(e_i) – высказывание, W – бесконечное множество, то (x)Р(х) – это высказывание, которое может быть либо истинным, либо ложным.

Пример: (x)Р(х) = (x)(х5) = Т, хD

Если переменная х в формуле с предикатом находится в области действия квантора, то она называется связкой. Область действия обозначается либо скобками, либо подчеркиванием.

Если переменная х в формуле с предикатом не находится в области действия квантора, то она называется свободной.

Пример: (у ((x)Р(х)  q(y))  Р(х)

Одна и та же переменная в формуле может быть и связкой и свободной. Формула замкнута, если в ней не существует свободных переменных. Замкнутая формула – это истинное или ложное высказывание. Если в формуле есть свободные переменные, то это функция, истинная или ложная, в зависимости от интерпретации. Высказывание – любая формула, не содержащая свободных переменных. Все формулы с предикатами разделяются на: тождественно-истинные (тавтологии), противоречия, выполнимые. Обозначенные формулы являются законами в логике предикатов. Для доказательства законов необходимо выполнить все интерпретации формул (что не возможно даже для конечных областей интерпретации)

Интерпретация: нужно поставить все возможные условия  Р(х)  все значения из Д – области интерпретации.

Теорема 1: Все формулы, содержащие только n – одноместных предикатов, выполнимы или общезначимы на некотором множестве М₁, содержащем не более 2ⁿ элементов.

Р₁(х),Р₂(х) . . . Р_n(х)

Если n = 1, то |М₂| = 2

n = 2, то |М₁| ~ 4

Доказательство: Пусть задана область интерпретации М (конечная или бесконечная).  Рi(х) – И или Л, это позволяет разделять множество М на 2 эксценсионала:

Каждое из множеств S₀,S₁ можно разделить на подмножество, на которое другой предикат либо И либо Л. Продолжая это разбиение, все множество М можно разделить на систему подмножеств.

М S = { S₀₀₀₀, S₀₀₀₁, . . . , S₁₁₁₁},

1 2 2ⁿ

в котором предикат р₁(е₁), . . . ,р_n(e_n) принимает значение «И» или «Л», если аргументы выбираются из соответствующих подмножеств.

Если мы выберем систему изn представителей, каждого из множеств, и объединим их в М₁, то мы можем утверждать, что при любой интерпретации, где предикатом:

Р(a_i) = «F» или «Т» = P(aj)/ajM₁

где a_i  S₁

M₁={a₁, . . . , a_n}

В результате разбиения множества М на классы, получим не более 2ⁿ класса, каждый из которых соответствует одному из 2ⁿ подстановок (выборов), n элементов из М, при которых предиката Р₁(е₁), . . . , Р_n(е_n) принимают значения «И» или «Л». Оставив только по одному представителю из каждого класса, получим множество представлений М₁, обладающих тем свойством, что для каждого предиката Р_j и любой подстановки элемента a_i.

Р_j(a_i) – найдется представитель из М₁­, на котором значение истинности предикатов совпадает, таким образом формула остается выполнимой или тождественно – истинной на ограниченном множестве М₁, состоящем из не более 2ⁿ элементов.

Таким образом, для интерпретации формулы с одноместными предикатами достаточно выбрать конечное множество, состоящее из произвольных элементов: М₁ = {1,2, . . . , 2ⁿ}.

Формула от двух предикат.

Ее область интерпретации М1 = {1,2}={а,в}

W - универсум

P – экстенсионал для предиката р(х)

Выделяются четыре подмножества:

S00 = ^P  ^Q

S10 = Q  ^P

S01 = ^Q  P

S11 = Q  P

В данном случае n = 2

m = 2² = 4

М₁ = {1,2,3,4}  четыре элемента из разных подмножеств (представители подмножеств)

Формула однозначимая, если она истинна на всех интерпретациях.

Для конечных множеств области интерпретации могут быть выбраны с количеством элементов меньше, чем 2ⁿ элементов.

Пример:

1. Только три подмножества:

М₁ = {1,2,3}

2. M₁ = {1,2,3}

3. М₁ = {1,2}

Для интерпретации формулы с одноместными предикатами общего вида:

F{p₁(x₁), . . . , p_n(x_n), Q}

1) Выбирается область интерпретации Д из 2ⁿ элементов: {1,2,3, . . . , 2ⁿ}.

2) Каждому предикатному символу P_i(x) ставится в соответствие истинностная функция _i(2ⁿ), где х  Д. Мы можем представить И, определяющее всевозможные значения функции: _i(1), _i(2), . . . _i(2ⁿ), каждому набору аргументов соответствует.

_i(1) _i(2) _i(2ⁿ)

0	0	0
0	0	1
1	1	1

3) Каждой переменной х_i приписывается значение из множества Д х_i  Д^2ⁿ. Это значение подставляем в _i(х_i)  _i(а).

4)Для каждой связанной переменной соответственно формируется конъюнкция, если они связаны квантором всеобщности  , т.е. (х):

(х)Р(х) (1) & (2) & . . . & (2ⁿ)

Общее определение алгоритма:

(х)Р(х)  (1)  (2)  . . .  (2ⁿ)

5) Константе присваивается все возможные значения из области Д: QД 2ⁿ значений.

6) Получим составное высказывание и для получения значения истинности нужно выполнить операции: &,,,,. И получим одно значение этой формулы = «И» и «Л».

На практике пункт 6) выполнять не будем, ограничимся построением формул высказывания. Такой метод, универсальный, конечный и эквивалентен применению ТИ в исчислении высказываний.

Пример: Проверить утверждение (является ли она общезначимой?)

(х)r(х)  (х)r(х) – общая формула логики предикатов.

Нужно выполнить интерпретацию

n = 1; m = 2 ; Д(1,2)

r(x)  (1),(2)

Подставляем в формулу:

(1) & (2)  (1) v (2)

Заменим символы:

1  а ; 2  в

(а) & (в)  (а)  (в)

а,в; (а); (в) – события отождествляем с аргументами

а&в  ав – тавтология  исходная формула общезначима.

Пример 2: (х)r(x)  (x)r(x)

(1) v (2)  (1) & (2)

a  в  a _* d

а_*в  ав – выполнимо  исходное тоже выполнимо.

Пример 3: r(x) & q(x)  (x)r(y) & q(x)

n = 2 ; m = 2² = 4 ; Д = {1,2,3,4}

r(x)  ₁(x)  ₁(1), ₁(2), ₁(3), ₁(4)

q(x)  ₂(x)  ₂(1), ₂(2), ₂(3), ₂(4)

r(x) & q(x)  x₁(i) q(x)  система высказываний

₁(1) & ₂(1)   ₁(i) & ₂(1)

₁(1) & ₂(2)   ₁(i) & ₂(2)

. . . . . . . . . . . . . . . . . . . . . . . . . .

₁(4) & ₂(4)   ₁(i) & ₂(4)

Все высказывания ₁(1), ₁(2), . . . , ₁(4) независимы, их можно обозначить через а,в,с,д, . . . ; А ₂(1) . . . ₂(4) . . . А,В,С,Д

Тогда система функций преобразуется в:

а  A  (a  в  c  d)A  1  все является тавтологией  исходная общезначима

Утверждение: Для интерпретации формул со свободными переменными х при проверке общезначимости выполнить замыкание формулы квантором всеобщности по этой переменной.

Если переменная в формулу входит связанная и свободная, то в одном из случаев ее стоимость переименовать и выполнить замыкание.

В данном примере на общезначимость проверяется формула:

(х)(r(х))q(x)  (y)r(y) & q(x)

Все переменные здесь связаны, поэтому эта формула – высказывание:

(₁(i) & ₂(i)   ₁(j) & ₂(i))

Пример 4: (х)((Р(х)  Q & P(y))

y – свободная переменная

х – связанная

(y)( x)((Р(х)  Q)  P(y))

n = 1; m = 2; Д = {1,2}; P(x)(1); (2)  a,в

1) сначала интерпретируем квантор по х (x)

(y) (((i)  Q)  Q & P(y)) / i = 1,2

(y) ( (i)  Q  Q & P(y))

(y) ( (i)  Q) = (y)(( (1)  Q)( (2)  Q))

=Q v а_*в – выполнима – формула не общезначима

2) интерпретация по у (y)

(х) (Р(х) Q  Q & (i)) /i = 1,2

y ( P(x)  Q)

(x)( P(x)  Q), (a  Q)(b  Q) = Q  ab

1. Кванторы подчиняются закону коммутативности:

(Kx)(Ky) F(p(x), q(y)) = (Ky)(Kx) F(P(x), q(x))

2. Свойство: расширение области действия кванторов.

1) формулы, содержащие свободные переменные:

Если переменные одинаковые, то одну надо переименовать.

2) формулы, не содержащие свободных переменных:

Р(х)₁(1), ₁(2), ₁(3), ₁(4) / М₁ = {1,2,3,4}

а в с d

q(x) ₂(1), ₂(2), ₂(3), ₂(4)

A B C D

(a  b  c  d)  (A  B  C  D) = (a  A)  (b  B)  (d ^ D)

- это тавтология  доказано; это доказательство для дизъюнкций.

Все законы логики высказывании распространяются и на логику предикат, в частности, правила де Моргана.

1) свободные переменные:

(р(х) & q(y)) = p(x)  q(y)

(р(х) & q(x)) = p(x)  q(x)

2) связанные переменные:

((Vx) p(x) = (х)(p(x))