1.1.2. Задания для самостоятельной работы

1.1. Шар радиуса R заряжен с объемной плотностью заряда  = ₀(1-r/R) , где ₀=const и r – расстояние от центра шара. Найти напряженность электрического поля внутри и вне шара, а также максимальное значение напряженности E_max и соответствующее ему значение расстояния r_m.

1.2. Шар радиуса R равномерно заряжен с объемной плотностью заряда . Найти поток вектора напряженности электрического поля через сечение шара, которое образовано плоскостью, отстоящей от центра шара на расстояние r₀< R.

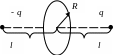1.3. Два точечных заряда q и -q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности электрического поля через круг радиуса R (см. рис.).

1.4. Внутри шара радиуса R, заряженного равномерно с объемной плотностью заряда , имеется сферическая полость радиуса r₀, центр которой совпадает с центром шара. Определить напряженность и потенциал электрического поля системы.

1.5. В центре сферы радиуса R, равномерно заряженной с поверхностной плотностью заряда , находится точечный заряд q. Определить напряженность и потенциал электрического поля внутри и вне сферы.

1.6. Система состоит из шара радиуса R, заряженного сферически симметрично, и окружающей среды, заполненной зарядом с объемной плотностью заряда  = /r, где  - постоянная, r – расстояние от центра шара. Найти заряд шара, при котором модуль вектора напряженности электрического поля вне шара не будет зависеть от r. Чему равна эта напряженность?

1.7. Заряд q распределен равномерно по объему шара радиуса R. Найти напряженность и потенциал электрического поля в центре шара, внутри и вне шара как функцию расстояния r от его центра.

1.8. Две концентрические сферы радиусами R₁ и R₂ (R₁ < R₂) равномерно заряжены зарядами q и –q соответственно. Определить напряженность и потенциал электрического поля при r  R₁, R₁  r  R₂ и r  R₂, где r – расстояние от центра сфер.

1.9. Внутри бесконечного круглого полого цилиндра радиуса R, равномерно заряженного так, что на единицу его длины приходится заряд , находится бесконечная нить, совпадающая с осью цилиндра. Нить равномерно заряжена с линейной плотностью заряда -. Определить напряженность и потенциал электрического поля внутри и вне цилиндра как функцию расстояния r от оси цилиндра в цилиндрической системе координат.

1.10. Бесконечный круглый цилиндр радиуса R равномерно заряжен с объемной плотностью заряда . Определить напряженность и потенциал электрического поля внутри и вне цилиндра как функцию расстояния r от оси цилиндра в цилиндрической системе координат.

1.11. В бесконечном круглом цилиндре радиуса R₁, равномерно заряженном с объемной плотностью заряда , имеется цилиндрическая полость радиуса R₂ (R₁ > R₂). Оси цилиндра и полости совпадают. Определить напряженность и потенциал электрического поля как функцию r цилиндрической системы координат при r  R₂, R₂  r  R₁ и r  R₁.

1.12. Бесконечная плоская плита толщиной а равномерно заряжена по объему с плотностью  . Найти напряженность электрического поля внутри и вне плиты.

1.13. Заряд электрона распределен в атоме водорода, находящемся в основном состоянии, с плотностью , где а – радиус боровской орбиты и r – расстояние от центра ядра. Найти напряженность электрического поля электронного облака в атоме водорода, а также величину ₀, выразив ее через заряд электрона е и радиус боровской орбиты а.

1.14. Пространство заполнено зарядом с объемной плотностью , где ₀ и  - положительные константы, а r - расстояние от центра данной системы. Найти напряженность электрического поля как функцию r. Исследовать полученное выражение при малых и больших r, т.е. при r³ <<1 и r³>>1.

1.15. Пространство между двумя концентрическими сферами. радиусы которых R₁ и R₂, (R₁ < R₂), заряжено с объемной плотностью  = /r². Найти полный заряд системы, напряженность и потенциал электрического поля внутри сфер, между сферами и вне сфер.

1.16. Найти напряженность и потенциал электрического поля сферы радиуса R, равномерно заряженной по поверхности. Заряд сферы q.