2.3.2. Задания для самостоятельной работы

2.44. Определить энергию единицы длины проводника с током J. Радиус проводника а, магнитная проницаемость материала проводника . Найти индуктивность единицы длины проводника.

2.45. Определить энергию магнитного поля и индуктивность, приходящиеся на единицу длины двухпроводной линии, по которой протекает ток плотностью j. Радиусы проводников одинаковы и равны а, расстояние между осями проводников d >> a, магнитная проницаемость материала проводников .

2.46. Решить задачу 2.45, если по проводникам протекает ток силой J, радиусы проводников одинаковы и равны а, а магнитная проницаемость проводников составляет ₁ и ₂ соответственно.

2.47. По двум бесконечным параллельным плоскостям, расстояние между которыми равно d, протекают противоположно направленные токи одинаковой линейной плотностью i. Пространство между плоскостями заполнено непроводящей средой с магнитной проницаемостью . Определить энергию магнитного поля, приходящуюся на единицу площади плоскостей.

2.48. По двум тонким бесконечным коаксиальным цилиндрам протекают одинаковые по величине и противоположные по направлению токи J. Радиусы цилиндров a и b > a. Определить энергию магнитного поля, приходящуюся на единицу длины, а также индуктивность единицы длины системы.

2.49. Для условия задачи 2.38 определить энергию единицы длины проводника.

2.50. Для условия задачи 2.12 определить энергию и индуктивность единицы длины проводника.

2.51. Для условия задачи 2.2 определить энергию и индуктивность единицы длины кабеля.

2.52. В условии задачи 2.2 магнитная проницаемость центральной жилы равна ₁, а пространства между жилой и оплеткой - ₂. Определить энергию и индуктивность единицы длины кабеля.

2.53. Для условия задачи 2.43 определить энергию магнитного поля единицы длины проводника с током.

2.54. Найти индуктивность длинного соленоида площадью сечения S и длиной l. Число витков, приходящихся на единицу длины соленоида, равно n, магнитная проницаемость сердечника - . Краевыми эффектами пренебречь.

2.55. N витков тонкого провода плотно намотаны на тороидальный сердечник из магнитного непроводящего материала с магнитной проницаемостью . Внутренний радиус катушки равен а, внешний – b, причем (b – a) << (a + b)/2. Определить индуктивность катушки.

2.4. Постоянный ток

2.4.1. Примеры решения задач

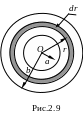
Пример. Однородная слабо проводящая среда с удельным сопротивлением  заполняет пространство между двумя коаксиальными цилиндрами радиуса а и b > a. Длина каждого цилиндра l. Найти сопротивление среды между цилиндрами.

Сопротивление среды между цилиндрами может быть рассчитано как непосредственно, так и с помощью закона Ома в дифференциальной форме.

Первый способ.

Рассчитаем сопротивление среды непосредственно. Выделим цилиндрический слой толщиной dr, как показано на рис. 2.9. Его сопротивление , где - площадь боковой поверхности цилиндра радиуса r. Тогда . Выполняя интегрирование по r от a до b, получаем .

Второй способ.

Пусть между цилиндрами поддерживается постоянная разность потенциалов U = ₁ - ₂. В проводящей среде при наличии поддерживаемой разности потенциалов между цилиндрами протекает ток плотности j, причем . При этом сила тока есть величина постоянная и определяется потоком вектора плотности тока через боковую поверхность цилиндра S с произвольным радиусом основания а ≤ r ≤ b:

.

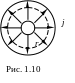
Т.к. векторы и перпендикулярны рассматриваемой боковой поверхности цилиндра в каждой точке (рис. 2.10), то потоки через основания равны нулю, т.е. . Учтем, что электрическая составляющая стационарного поля описывается законами электростатики, и воспользуемся теоремой Гаусса:

,

где  - заряд единицы длины цилиндров (заряд, протекающий через проводящую среду, пополняется за счет работы источника тока). Таким образом, напряженность электрического поля в среде . Тогда

.

С другой стороны,

.

Следовательно, и . Отсюда, в соответствии с законом Ома, получаем .