2.3. Энергия магнитного поля. Индуктивность проводников

2.3.1. Примеры решения задач

Пример. Определить энергию магнитного поля, приходящуюся на единицу длины двухпроводной линии, по которой протекает ток J. Радиус первого проводника а, второго - b, расстояние между осями проводников d >> a, b, магнитная проницаемость материала проводников . Найти индуктивность единицы длины линии.

Индуктивность единицы длины линии может быть определена в соответствии с выражением (2.30) вычислением потока, пронизывающего плоскость контура единичной

д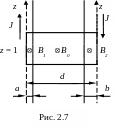 лины, ограниченного осями токов (см. рис.2.7). При этом энергия, приходящаяся на единицу длины линии (разумеется, L – индуктивность единицы длины линии). Возможен и другой способ расчета требуемых величин – непосредственное вычисление энергии единицы длины линии с последующим определением индуктивности.

Первый способ.

Из рис. 2.7 видно, что полный поток Ф = Ф₁ + Ф₂ + Ф₀, где Ф₁ и Ф₂ – потоки, пронизывающие сечения первого и второго проводников соответственно и Ф₀ – поток, пронизывающий область между проводнимками.

Используя результаты, полученные в примерах 2 п.2.1.1 и 1 п.2.2.1, индукцию магнитного поля в выделенных областях можно представить в виде:

, , .

Подчеркнем, что в выражениях для В₁ и В₂ r₁ и r₂ отсчитываются от осей соответствующих токов (для значения В₀ отсчет r не имеет значения).

Т.к. векторы и перпендикулярны плоскости, в которой лежат оси токов J₁ и J₂, то потоки, пронизывающие поверхность рассматриваемого контура единичной длины,

, ,

.

Учитывая, что d >> a и b, получаем и . Тогда

.

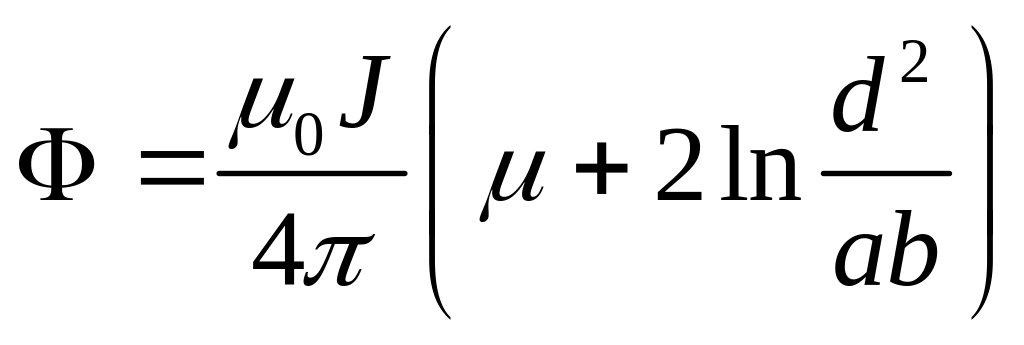Следовательно, 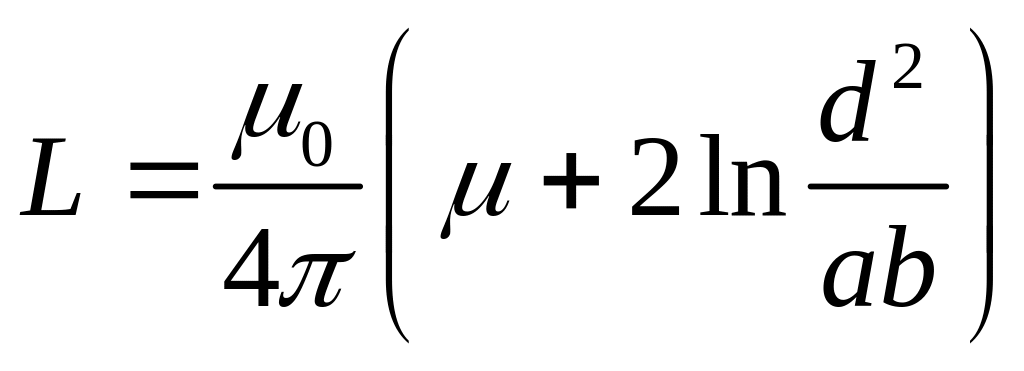и .

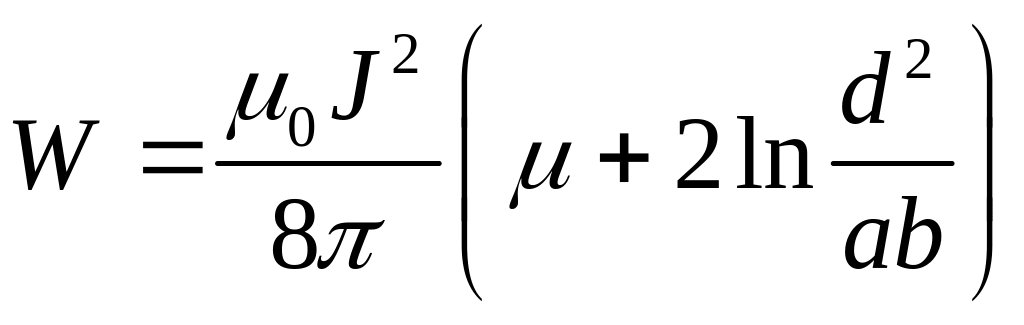Второй способ.

Вычислим энергию магнитного поля единицы длины линии с помощью формулы (2.28), в которой , т.е. выражение для энергии единицы длины линии принимает вид:

,

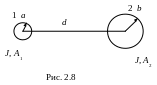
где , А₁ – векторный потенциал, создаваемый токами J и –J в области первого проводника, а А₂ – в области второго проводника. Здесь

А₁ = А₁₁ + А₂₁ и А₂ = А₂₂ + А₁₂,

причем А₁₁ и А₂₂ - векторные потенциалы, создаваемые токами J и -J в области первого и второго проводников соответственно, А₂₁ – векторный потенциал, создаваемый током -J в области первого проводника, а А₁₂ – векторный потенциал, создаваемый током J в области второго проводника.

Для указанных векторных потенциалов воспользуемся результатами, полученными в примере п. 2.2.1:

при r₁  a и при r₁  a;

при r₂  b и при r₂  b.

Здесь r₁ и r₂ отсчитываются от осей соответствующих токов, наличие постоянной С в выражениях для А₂₂ связано с тем, что потенциал отсчитывается от оси первого проводника. Тогда, полагая A₂₂ = 0 при r₂ = d , получаем и

при r₂  b, при r₂  b.

Учитывая, что a, b << d и поэтому пренебрегая изменением векторных потенциалов А₁₁ при r₁ > a и А₂₂ при r₂ > b в областях, занятых токами ^_J и J соответственно, получаем:

и .

Таким образом

и .

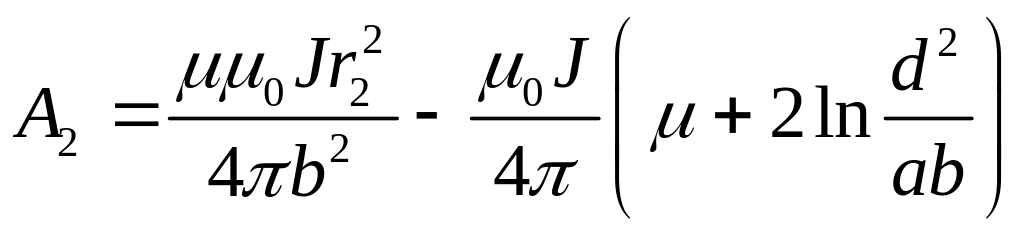Тогда энергия, приходящаяся на единицу длины линии, будет определяться как

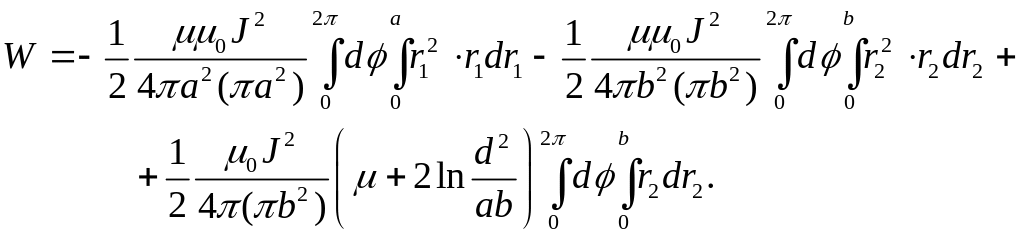
Выполняя интегрирование, получаем

и .