Равновесие

Рассматривая совместно кривую предложения Лукаса (уравнение [6.21]) и кривую агрегированного спроса (уравнение [6.10], ) находим решения для и :

, (6.22)

. (6.23)

Далее, используя (6.22), можно найти . Ex post, после того как величина становится известной, правая и левая часть (6.22) должны быть равны. Тогда ex ante, до того как становится известной, ожидания правой и левой части должны быть равны:

, (6.24)

или

. (6.25)

Используя (6.25) и тот факт, что , уравнения (6.22) и (6.23) можно переписать в виде:

, (6.26)

. (6.27)

Уравнения (6.26) и (6.27) представляют основные результаты модели: наблюдаемая компонента агрегированного спроса, , воздействует только на цены, а ненаблюдаемая компонента, , обладает реальным эффектом. Например, рассмотрим неожиданное увеличение , т.е. реализацию на уровне выше ожидаемого среднего при данном распределении. Рост предложения денег увеличивает агрегированный спрос, а значит, приводит к сдвигу вправо кривой спроса на каждое благо. Т.к. рассматриваемое изменение является ненаблюдаемым, то каждый производитель будет считать, что имеющий место рост спроса на его товар частично отражает шок относительных цен. Таким образом, производители увеличат выпуск.

Эффекты наблюдаемого увеличения существенно отличаются. Например, рассмотрим эффекты сдвига вверх всего распределения , при неизменной реализации . В данном случае каждый производитель относит рост спроса на свою продукцию к последствиям роста денежной массы, а значит, не будет менять объем производства. При этом, конечно, шоки вкусов и предпочтений приводят к изменению относительных цен и объемов выпуска разных товаров, также как это имело место в случае ненаблюдаемых шоков. Однако в среднем реальный выпуск при этом не меняется. Таким образом, наблюдаемые шоки агрегированного спроса воздействуют только на цены.

В завершении, мы должны выразить коэффициент в терминах исходных параметров модели, а не в терминах дисперсий и . В соответствии с уравнением (6.20), . Из уравнения (6.26) вытекает, что . Уравнение спроса (6.7) и уравнение предложения (6.21) можно использовать в определении , дисперсии . А именно, подставляя в уравнение (6.7) мы получим . Кроме того, можно переписать (6.20) в виде . Выражая из последних двух уравнений, имеем . Таким образом, мы получаем, что .

Подставляя полученные выражения для и в уравнение (6.20), определяющее , получаем:

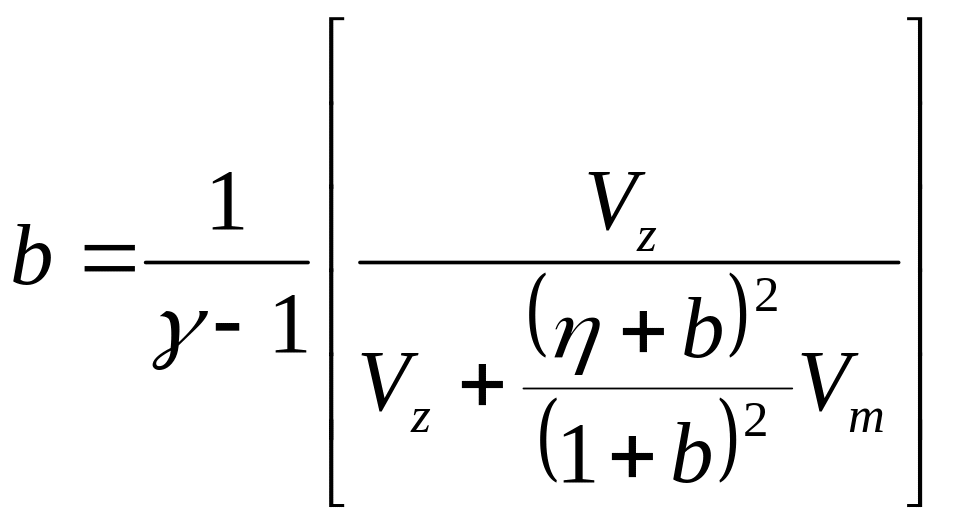. (6.28)

Уравнение (6.28) определяет коэффициент в терминах , и . Таким образом, теперь модель построена до конца. Несложно показать, что возрастает с ростом и убывает с ростом . В частном случае, когда , мы можем получить аналитическое решение для :

. (6.29)

И, наконец, из того, что и , следует, что и являются линейными функциями от и . Т.к. и являются независимыми, и также будут независимыми. Линейная функция нормально распределенных случайных величин сама является нормально распределенной случайной величиной. Следовательно, и имеют нормальное распределение. Это подтверждает обоснованность введенных выше предположений относительно данных переменных.