6.6 Фиксированные цены Модель

Внесем изменения в модель из предшествующего раздела. Предположим, что индивиды должны устанавливать одинаковые цены на два периода вперед. Т.е., во введенной ранее терминологии, цены являются не только предопределенными, но и фиксированными.

Кроме того, мы привнесем в модель еще два небольших изменения. Во-первых, мы предположим, что индивиды, которые устанавливают цены в периоде , делают это для периодов и , а не периодов и . Это упростит анализ, не повлияв существенно на результаты. Во-вторых, модель будет значительно проще решить, если определить конкретный процесс динамики . Пусть это будет процесс случайного блуждания:

, (6.59)

где - это белый шум. Отличительной характеристикой данного процесса является то, что инновации в (т.е. ) обладают продолжительным по времени воздействием на уровень переменной.

Обозначим за - цену, которую индивид устанавливает в момент времени . Мы снова будем придерживаться принципа эквивалентности детерминированному случаю, полагая, что индивиды стараются, на сколько это возможно, приблизить цены к оптимальному уровню. В данном случае это означает, что

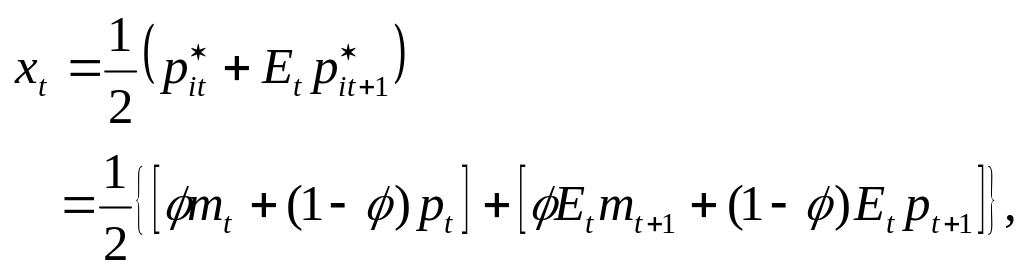(6.60)

где при переходе ко второй строке используется тот факт, что .

Т.к. в каждый период времени устанавливается половина цен, то будет равно среднему из и . Кроме того, если следует процессу случайного блуждания, то равно . С учетом этого, уравнение (6.60) можно привести к виду:

. (6.61)

Выражая отсюда , получаем:

(6.62)

Уравнение (6.62) является ключевым уравнением модели.

Уравнение (6.62) определяет в терминах , и ожидаемой величины . Чтобы решить модель, необходимо каким-то образом избавиться от ожиданий . Мы рассмотрим два способа решения модели: с использованием метода неопределенных коэффициентов и с использованием лаговых операторов. Как правило, метод неопределенных коэффициентов несколько проще. Но есть ситуации, когда его использование сопряжено с определенными трудностями. В таких случаях использование лаговых операторов оказывается весьма полезным.

Метод неопределенных коэффициентов

Как обсуждалось в разделе 4.6, основная идея метода неопределенных коэффициентов состоит в подборе общей функциональной формы решения с последующим поиском конкретных значений коэффициентов на основе самой модели. В рассматриваемой здесь модели, в периоде две переменные уже даны – это денежная масса, , и установленные в предшествующем периоде цены, . Кроме того, модель является линейной. Так что вполне оправданной будет пробное предположение, что должна быть линейной функцией от и :

. (6.63)

Наша задача состоит в определении значений , и , которые решают данную модель.

Перед тем как приступить к поиску , и , можно упростить вычисления, если вначале использовать наше знание модели для того, чтобы дополнительно ограничить (6.33). Мы нормализовали к нулю константу в уравнении, определяющем оптимальные цены, . Как следствие, в равновесии с гибкими ценами должно быть равным 0, а все цены должны быть равны . С учетом этого, рассмотрим ситуацию, когда и равны. Если в периоде индивиды, устанавливающие цены, также установят их на уровне , то экономика окажется в равновесии с гибкими ценами. Кроме того, т.к. следует процессу случайного блуждания, у индивидов, устанавливающих цены в периоде , нет оснований полагать, что будет в среднем выше или ниже чем . Следовательно, будет в среднем соответствовать . Так что в данной ситуации и будут равны , и индивиды установят цены . Для (6.63) это означает, что

(6.64)

для любых .

Для соблюдения (6.64) требуется выполнение двух условий. Во-первых, должно соблюдаться . В противном случае (6.64) не будет верно для любых . Во-вторых, если мы установим , соблюдение (6.64) дополнительно потребует, чтобы . Подставляя данные условия в (6.63), получаем:

. (6.65)

Наша задача теперь состоит в поиске значения , решающего модель.

Уравнение (6.65) может быть записано для любого периода. В частности, . Тогда формируемые в периоде ожидания - это ожидания , что просто равно . Подставляя в последнее выражение из (6.65), получаем:

(6.66)

В свою очередь, подстановка полученного выражения в (6.62) дает:

(6.67)

Если агенты, устанавливающие цены, верят в то, что является линейной функцией от и в форме, предполагаемой (6.65), то, максимизируя прибыль, они действительно будут устанавливать свои цены как линейные функции от данных переменных. Если мы найдем решение модели, два данных линейных уравнения должны быть одинаковыми. Сравнивая (6.65) и (6.67), можно сделать вывод, что для их совпадения требуется выполнение двух условий:

, (6.68)

и

. (6.69)

Уравнение (6.68) является квадратным по . Его решение определяется корнями

. (6.70)

Несложно показать, что эти значения удовлетворяют также и условию (6.69). С учетом определения константы в (6.62), значения можно переписать в виде:

, (6.71)

. (6.72)

Однако, имеет смысл рассматривать только одно из значений , а именно . Если , то . Экономическая динамика при этом будет устойчивой. Напротив, в случае, когда . Динамика экономики будет при этом неустойчивой: незначительный шок устремит выпуск в плюс или минус бесконечность. В результате, предположения, положенные в основу модели (например, предположение, что продавцы не рационируют покупателей) не будут соблюдаться. По этой причине, мы рассмотрим лишь величину .

Таким образом, выражение (6.65) для является решением модели: если индивиды, устанавливающие цены, верят, что другие используют то же самое правило, они сами будут считать рациональным использовать именно его.

Теперь мы можем описать динамику выпуска. Величина равна , что в свою очередь равно . С учетом уравнения динамики , (6.65), получаем:

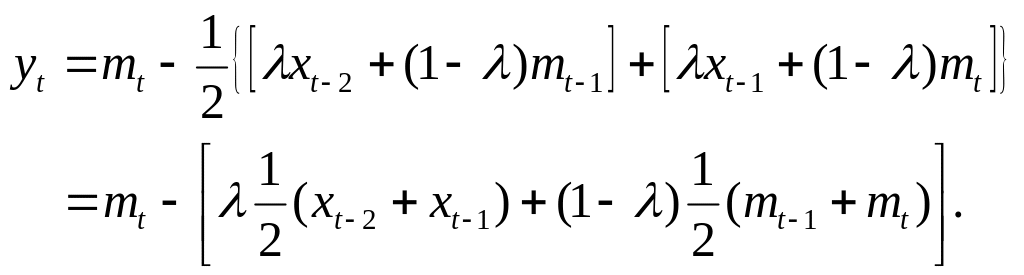(6.73)

Используя то, что , и тот факт, что , последнее выражение можно свести к следующему простому виду:

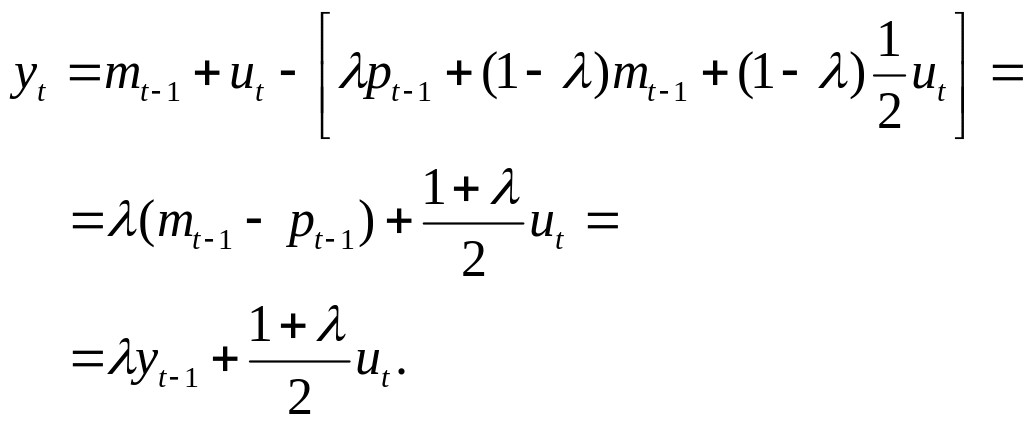(6.74)

Следствия

Уравнение (6.74) представляет основные результаты модели. Т.к. является положительной величиной (что верно в случае, если ), из уравнения (6.74) следует, что шоки агрегированного спроса будут характеризоваться продолжительными эффектами на выпуск – эффектами, которые будут наблюдаться даже после того как все индивиды изменят свои цены. Предположим, что экономика первоначально находится в состоянии равновесия с гибкими ценами (т.е. находится на стационарном нулевом уровне), и рассмотрим эффект положительного шока . В период времени, когда происходит данный шок, не все индивиды могут подстроить свои цены, так что вполне естественно, что при этом возрастает. Как следует из (6.74), . В следующем периоде, несмотря на то, что теперь оставшиеся индивиды могут подстроить цены, не возвращается к своему нормальному уровню даже в отсутствии новых шоков: в соответствии с (6.74), . И так постепенно выпуск возвращается к своему нормальному уровню, при условии, что на каждом этапе.

Реакция уровня цен на шок представляет собой как бы обратную сторону реакции выпуска. Уровень цен возрастает на в первом периоде, а затем на долю оставшегося расстояния от в каждом последующем периоде. Таким образом, в экономике будет наблюдаться инерция уровня цен.

Источником продолжительных реальных эффектов монетарных шоков вновь выступает нежелание индивидов в полной мере менять свои относительные цены. Вспомним, что , и что только в случае, когда . Так что плавная подстройка цен будет иметь место, только если оптимальные цены являются возрастающей функцией уровня цен. Предположим, что каждый индивид решает полностью подстроить свою цену при первой же возможности. В данном случае, индивиды, устанавливающие цены в периоде, когда происходит шок, сразу же подстроят свои цены на всю величину шока. Оставшиеся индивиды сделают то же в следующем периоде. Таким образом, вырастет на величину в начальном периоде и вернется к своему нормальному уровню в следующем периоде.

Однако представленная быстрая подстройка не может иметь место в равновесии в случае, когда меньше 1. Действительно, рассмотрим индивидов, подстраивающих свои цены сразу же. Как предполагается, все цены будут подстроены ко второму периоду, так что для данного периода каждый индивид выбирает оптимальную цену. Но если , то оптимальная цена будет низкой, когда уровень цен низкий. Не все цены могут подстроиться сразу же в ответ на шок. Так что цены, подобранные оптимальным образом в период, когда происходит шок, будут ниже оптимального уровня в следующем периоде. Получается, что данным индивидам не имеет смысла полностью подстраивать цены в первоначальном периоде. Но это в свою очередь означает, что оставшимся индивидам также будет невыгодно полностью приспосабливать свои цены в следующем периоде. И знание, что полная подстройка не будет наблюдаться и в будущем сдерживает реакцию индивидов, подстраивающих свои цены в период когда происходит шок. Окончательным результатом описанного вперед и назад смотрящего взаимодействия будет плавный процесс подстройки, представленный уравнением (6.65).

Таким образом, также как и в модели, где цены предопределены, но не фиксированы, степень неполноты номинальной подстройки на уровне агрегатов может оказаться сильнее, чем можно было бы предположить первоначально лишь на том основании, что не все цены подстраиваются в каждом периоде. Действительно, степень негибкости агрегированного уровня цен будет еще выше в данной ситуации, когда наблюдается последействие даже после того, как все цены изменились. И снова низкое значение , т.е. высокая степень реальной жесткости, является необходимым для данного результата условием. Если равно 1, т.е. равно 0, то каждый индивид будет полностью подстраивать свою цену при первой же возможности. Если превышает 1, то является отрицательным, так что изменяется сильнее, чем в период, следующий за шоком, и процесс возвращения к долгосрочному равновесию будет носить характер колебаний.

Лаговые операторы

Альтернативным и более общим подходом к решению модели является использование лаговых операторов. По определению, лаговый оператор ставит в соответствие любой переменной ее же собственное значение, взятое с лагом: .

Чтобы увидеть все положительные стороны работы с лаговыми операторами, рассмотрим нашу модель без предположения, что следует процессу случайного блуждания. Мы можем отталкиваться от уравнения (6.60). Если предпринять те же самые действия, что и в случае вывода уравнения (6.62), но не предполагать при этом, что , то мы получим следующее уравнение:

, (6.75)

где константа - та же, что и прежде. Действительно, (6.75) принимает простой вид (6.62), если .

На первом этапе нужно переписать данное выражение в лаговых операторах. Величина может быть связана с с помощью лагового оператора: . Воспользуемся правилом, согласно которому в случае, когда применяется к выражению, содержащему ожидания, то происходит лаговый сдвиг самой переменной, но не периода, в котором формируются ожидания. Мы можем представить в виде .¹⁴ Используя обозначение для обратной функции, мы можем записать . Аналогично, . С учетом этого, можно переписать (6.75) в виде:

, (6.76)

или

. (6.77)

Здесь обозначает оператор тождественного преобразования (т.е. для любого ). Так что представляет сокращенную форму записи для выражения , а - сокращенную форму записи для .

Заметим, что может быть «разложено» на , где как и раньше определяется выражением (6.70). Таким образом, мы получаем следующее уравнение:

. (6.78)

Данная форма записи, содержащая лаговый оператор, может быть проинтерпретирована естественным образом: выражение является сокращенной формой записи для за вычетом произведения на обратный лаговый оператор, примененный к . Т.е., данное выражение равно . С учетом определения , несложно показать, что (6.78) и (6.77) являются эквивалентными формами записи.

Так же как и в первом методе, чтобы найти решение, нам нужно избавиться от члена, содержащего ожидания относительно будущего значения эндогенной переменной. неявным образом присутствует в левой стороне (6.78), что определяется оператором . «Поделим» правую и левую сторону на . Это даст тот же результат, что и применение оператора . Действительно, произведение операторов и дает тождественный оператор . Таким образом, в левой части останется . В правой части будет стоять произведение операторов и , что даст следующий оператор: .¹⁵ В итоге, выражение (6.78) переписывается в виде:

. (6.79)

Или без лаговых операторов:

. (6.80)

Уравнение (6.80) характеризует динамику устанавливаемых цен в зависимости от экзогенного процесса, определяемого предложением денег. Для того, чтобы описать динамику агрегированного уровня цен и выпуска, требуется просто подставить полученное выражение в формулы, определяющие и (т.е. и ).

В частном случае, когда следует процессу случайного блуждания, все ожидаемые величины будут равны , так что (6.80) принимает простой вид:

. (6.81)

Несложно показать, что выражение (6.68), с учетом того, что , сводится к уравнению (6.65), . Таким образом, если следует процессу случайного блуждания, мы получаем тот же результат, что и выше. Но при этом мы также нашли решение модели для общего процесса .

Хотя использование лаговых операторов может показаться довольно замысловатой процедурой, это не более чем компактный способ проведения соверешенно обычных действий. Можно было бы вначале, путем нехитрых алгебраических преобразований, вывести (6.77), в виде, не содержащем лаговых операторов. Затем, с учетом того, что (6.77) должно соблюдаться для любого периода времени, можно записать

(6.82)

для любого .¹⁶ Уравнение (6.82) можно использовать следующим образом: если к левой части для прибавить левую часть для , умноженную на , затем прибавить левую часть для , умноженную на , и т.д., то это должно быть равно выражению в правой части для плюс выражение в правой части для , умноженное на , плюс выражение в правой части для , умноженное на , и т.д. В итоге это даст (6.80). Так что использование лаговых операторов вовсе не является обязательным – это просто упрощает запись и направляет ход решения.¹⁷

Модель Тейлора и инфляционная инерция

Как отмечалось в главе 5, современная кейнсианская интерпретация проблемы выбора между выпуском и инфляцией исходит из того, что инфляция обладает определенной степенью инерции. Т.е., политика агрегированного спроса может добиться снижения инфляции только ценой периода низкого выпуска и высокой безработицы. Подобного рода представление лежит в основе объяснения кейнсианцами динамики выпуска в периоды проведения программ снижения инфляции (например, в Соединенных Штатах в начале 1980-ых). Как было показано выше, модель Тейлора демонстрирует определенную инерцию динамики уровня цен: пока он полностью подстраивается под монетарный шок, выпуск на протяжении длительного периода значительно отклоняется от своего нормального уровня. В результате, часто утверждается, что модель Тейлора демонстрирует инфляционную инерцию.

В работе Fuhrer and Moore (1995) показывается, что это утверждение неверно (см. также Ball, 1994a). Действительно, вернемся к уравнению ценообразования (6.60), . Т.к. , мы получаем, что

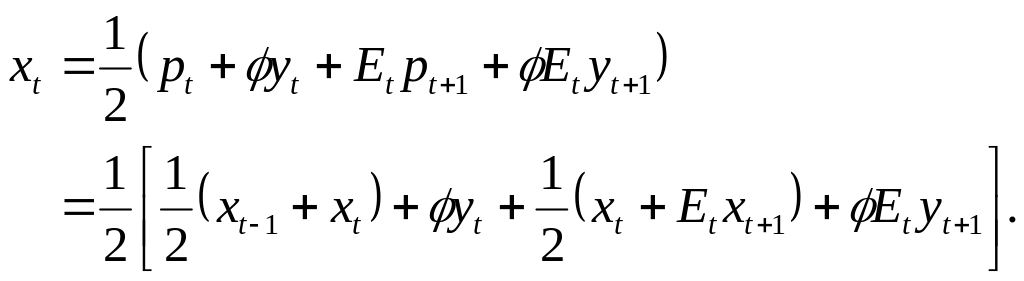(6.83)

Выражая из данного уравнения , получаем:

. (6.84)

Чтобы получить выражение для инфляции, обозначим . Умножая правую и левую часть (6.84) на 2 и вычитая с каждой стороны, получаем:

. (6.85)

Если мы обозначим , то (6.85) можно переписать в виде:

. (6.86)

Основной чертой (6.86) является то, что величина появляется с отрицательным знаком: высокие уровни выпуска связаны с падением инфляции. Таким образом, сама по себе постепенная подстройка цен (и заработной платы) вовсе не создает препятствий на пути снижения инфляции.¹⁸

Можно дать интуитивное объяснение тому факту, что в модели Тейлора снижение инфляции не связано со снижением выпуска ниже нормального уровня. Обратим внимание на то, что ситуация, когда меньше , соответствует ситуации, когда выше среднего из и . При этом индивид, устанавливающий цену в период , не выберет выше среднего из и в случае, когда выпуск ниже нормального уровня. Напротив, если выпуск ниже нормального уровня, то это побуждает индивидов устанавливать ниже среднего из и . Т.е., в рассматриваемой модели снижение выпуска ниже нормального уровня приводит к росту инфляции.¹⁹