Вопрос 13.

Численное интегрирование. Метод прямоугольников.

Потребность в приближенном вычислении интегралов возникает тогда, когда не существует или неизвестен метод отыскания точного значения интеграла или когда этот метод является сложным или. В случае задания функции в табличной форме приближенные методы являются единственными.

Все приближенные методы основаны на следующем положении: рассматривая интеграл как площадь криволинейной трапеции, можно получить его приближенное значение, если вычислить площадь другой трапеции, ограничивающая линия которой по возможности мало отличается от заданной. В зависимости от вида этой кривой составлены различные формулы приближенных вычислений интеграла.

Методы прямоугольников

На каждом частичном интервале [x_i , x_i+1 ] заменяют аппроксимирующую функцию f(x) полиномом нулевой степени, т.е. константой, равной значению функции. Здесь возможны, как минимум, три варианта.

1. Значение функции является левой точкой частичного интервала

[x_i , x_i+1 ]. Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

. (1)

Ее называют первой формулой прямоугольников или формулой прямоугольников с левыми ординатами.

2. Значение функции является правой точкой частичного интервала

[x_i , x_i+1 ]

Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

. (2)

Ее называют второй формулой прямоугольников или формулой прямоугольников с правыми ординатами.

Рис.1. Метод левых ординат	Рис.2. Метод правых ординат	Рис.3. Метод средних

3. Значение функции является средней точкой частичного интервала

[x_i , x_i+1 ] (Рис.3). Тогда значение интеграла принимается равным сумме площадей элементарных прямоугольников, вычисляемой по формуле

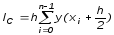. (3)

Ее называют третьей формулой прямоугольников или формулой метода средних.

Вопрос 14. Численное интегрирование. Метод трапеций.

На каждом частичном интервале [x_i , x_i+1 ] заменяют аппроксимирующую функцию f(x) полиномом Лагранжа первой степени, т.е. применяют линейную интерполяцию. График функции в этом случае представляет ломаную линию, соединяющую точки (x_i, y_i ) (Рис.4). В этом случае площадь всей фигуры складывается из площадей элементарных прямоугольных трапеций, равных s_i=h(y_i-1+y_i)/2 (i=1,2,…,n) . Сумма этих площадей и представляет формулу трапеций

.

Вопрос 15. Численное интегрирование. Метод Симпсона.

Отрезок интегрирования [a , b] разбивают на четное количество n=2m равных интервалов с шагом

На каждых двух соседних интервалах [x_i-1 , x_i ] и [x_i , x_i+1 ] (i=1,2,…,n-1) , начиная с первого, заменяют функцию полиномом Лагранжа или Ньютона второй степени, т.е. параболой, проходящей через три точки с координатами

(x_i-1, y_i-1 ) , (x_i, y_i ) , (x_i+1, y_i+1 ) и с осью симметрии, параллельной оси ординат (Рис.5).

Площадь каждой пары интервалов равна s_i=(y_i-1+4y_i+y_i+1)h/2 . Сумма этих площадей и представляет формулу Симпсона

Рис.5. Метод Симпсона