(Вопрос 1) Абсолютная и относительная погрешности суммирования и вычитания чисел. Источники и классификация погрешностей
Источниками возникновения погрешности:
Неточность математического описания (например экспериментальные начальные данные).
Неточность численного метода (ограничения количества арифметических операций вычисления).
Конечная точность машинного счета.
Виды погрешностей:
Неустранимая погрешность – неточность задания числовых данных и погрешность математической модели.
Погрешность метода – считается устранимой.
Вычислительная погрешность – или погрешность округлений.
Абсолютная и относительная погрешности. Форма записи данных
Абсолютная.
x – точное значение некоторой величины.
x- известное приближение к нему.
( x) - абсолютная погрешность x .
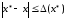
Имеют ту же размерность, что х.
Относительная.
(x) - относительная погрешность.
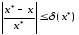
Безразмерна и выражена в долях или процентах.
Вычислительная погрешность
- абсолютная погрешность.
- относительная погрешность.
Погрешность
суммирования чисел:
Имеем
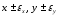
Абсолютная
погрешность:
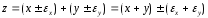
Относительная погрешность:
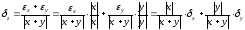
Погрешность вычитания:
Абсолютная погрешность
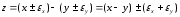
Относительная погрешность
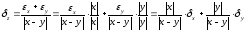
Вопрос 2. Абсолютная и относительная погрешности умножения и деления чисел.
Можно не учитывать
Абсолютная
погрешность
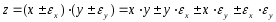
Относительная погрешность
Деления
Абсолютная погрешность
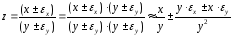
Относительная погрешность
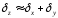
Вопрос 3. Аппроксимация дискретных данных Метод наименьших квадратов
Аппроксимация – замена функции другой более удобной (приближенной).
Метод наименьших квадратов применяют, когда необходимо вывести формулу аппроксимирующей кривой, описывающей зависимость, полученную в результате, например, эксперимента. (экспериментальные данные получают с погрешностью).
Кривая не проходит через экспериментальные точки, но учитывает исследуемую закономерность, сглаживая случайные выбросы.
В качестве аппроксимирующей функции может использоваться линейная комбинация F(x) любых функций:
F(x)= a0f0(x)+a1f1(x)+ … + anfn(x) ,
f0(x),
f1(x),…,
fn(x)
- набор любых функций (базисные).
a0 ,a1 ,… ,an - набор коэффициентов.
Требуется определить коэффициенты a0 ,a1 ,… ,an полинома
P (x)=a0+a1x+ … +anxn
таким образом, чтобы сумма S квадратов отклонений полинома P(x) от значений yi аппроксимируемой функции в заданных точках была бы минимальной, т.е.
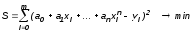
Вопрос 4. Интерполяция дискретных данных. Интерполяционный многочлен Лагранжа.
Интерполяция – способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
В различных областях науки и техники часто возникает задача приближенной замены некоторой зависимости f(x) другой функцией (x) таким образом, чтобы отклонение функции (x) от f(x) на заданном отрезке [a , b] было наименьшим. Функция (x) называется аппроксимирующей, а сама процедура замены – аппроксимацией. Если приближение строится на дискретном множестве точек xi, то такая аппроксимация называется точечной. Одним из основных типов точечной аппроксимации является интерполирование.
Задача интерполирования: для функции y=f(x) построить функцию, принимающую в заданных точках xi, называемых узлами интерполирования, те же значения yi, что и функция f(x), т.е. (x)=yi , (i=0,1,…,n).
Функция y=f(x) может быть задана в виде координат точек xi и yi, полученных например экспериментальным путем.
Пусть на отрезке [a , b] в неравноотстоящих n+1 узлах x0, x1, . . . , xn известны значения функции y0=f(x0) , y1=f(x1) , . . . , yn =f(xn) . Требуется построить многочлен L(x) так, чтобы в узлах x0, x1, . . . , xn его значения совпадали со значениями заданной функции, т.е. L(x0)=y0 , L(x1)=y1 , . . . ,L(xn)=yn .
Будем искать многочлен степени не выше n
L(x)=a0+a1x+a2x2+. . . +anxn , (1)
где a0, a1, . . . , an - постоянные коэффициенты, которые требуется найти.
Подставим вместо x значения x0, x1, . . . , xn, а вместо L(x) их значения y0, y1, . . . , yn. Получим систему уравнений
a0+a1 x0+ a2 x02+ + an x0n = y0
a0+a1 x1+ a2 x12+ + an x1n = y1 (2)
. . . . . . . . . . . .
a0+a1 xn+ a2 xn2+ + an xnn = yn
Решение этой системы позволит определить все коэффициенты a0, a1, . . . , an многочлена (1). Так и поступают, когда требуется многократно использовать многочлен (1). Для разового использования гораздо быстрее и удобнее воспользоваться многочленом в форме Лагранжа, который предложил линейную комбинацию многочленов степени n:
L(x)=y0 l0(x)+ y1 l1(x)+ . . . + yn ln(x) (3)
Потребуем, чтобы каждый многочлен li(x) обращался в нуль во всех узлах интерполяции, за исключением одного i-го, где он должен равняться единице. Этим условиям отвечает многочлен вида
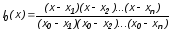(4)
Действительно, при x=x0 l0(x0)=1 . При всех остальных значениях x=x1, x2, . . . , xn числитель выражения (4) обращается в нуль. По аналогии с (4) получим
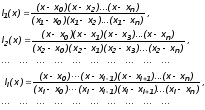(5)
Подставляя в (3) выражения (4) и (5), получим
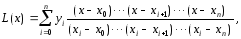
или в более компактной записи
(6)
Эта формула называется интерполяционным многочленом Лагранжа. Она позволяет избавиться от необходимости вычисления коэффициентов a0, a1, . . . , an в (1) путем решения системы (2), а использовать только известные значения узлов интерполяции. Непременное условие – отсутствие совпадающих узлов.