16.Дисперсия, среднее квадратичное отклонение.

Во многих практически важных случаях существенным является вопрос о том, насколько велики отклонения   случайной величины от ее математического ожидания.     Предварительно рассмотрим пример. Пусть две случайные величины   и   заданы следующими рядами распределения  

Значения	-0,2	-0,1	0,1	0,2
Вероятности p(x)	0,25	0,25	0,25	0,25

 

Значения	-50	-40	40	50
Вероятности p(x)	0,25	0,25	0,25	0,25

   Легко убедится в том, что математические ожидания этих величин одинаковы и равны нулю:  

   Однако разброс значений этих величин относительно их математического ожидания неодинаков. В первом случае значения, принимаемые случайной величиной  , близки к ее математическому ожиданию, а во втором случае далеки от него. Для оценки разброса (рассеяния) значений случайной величины около ее математического ожидания вводится новая числовая характеристика - дисперсия.     Дисперсией   случайной величины   называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *:

(43)

   Пусть   - дискретная случайная величина, принимающая значения x₁, x₂, ..., x_n соответственно с вероятностями p₁, p₂, ..., p_n. Очевидно, случайная величина   принимает значения

с теми же вероятностями p₁, p₂, ..., p_n. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем

(44)

   Если же   - случайная величина с плотностью распределения  , то по определению

(45)

   Принимая во внимание определение дисперсии и свойства математического ожидания, имеем

   Так как   и   - постоянные, то используя свойства математического ожидания, получим

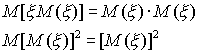
   Следовательно,

   Откуда окончательно находим

(46)

   Рассмотрим теперь свойства дисперсии.     1°. Дисперсия постоянной равна нулю. (Доказательство)     2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

(47)

(Доказательство)

   3°. Если   и   - независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

(48)

(Доказательство)

   Средним квадратическим отклонением   случайной величины   называется корень квадратный из ее дисперсии:

(49)

   Среднее квадратическое отклонение   имеет ту же размерность, что и случайная величина  .     Пример 1. Cлучайная величина   - число очков, выпадающих при однократном бросании игральной кости (см. § 3, п.1, пример 1). Определить: математическое ожидание, дисперсию и средне квадратическое отклонение (Решение)     Пример 2. Cлучайная величина   - число наступления события A при одном испытании, причем P(A)=p (см. § 3, п.1, пример 2). Найти математическое ожидание и дисперсию. (Решение)     Пример 3. Cлучайная величина m - число наступления события A в n независимых опытах, причем вероятность наступления события A в каждом опыте равна p. Найти M(m), D(m) и   (Решение)     Пример 4. Пусть   - случайная величина распределенная по закону Пуассона

[См. формулу (17)]. Найти:   (Решение)     Пример 5. Пусть   - случайная величина, имеющая равномерное распределение с плотностью

[См. формулу (27)]. Найти математическое ожидание, дисперсию и средне квадратическое отклонение cлучайной величины. (Решение)

   Пусть   - нормально распределенная случайная величина, с параметрами a и   (см. § 3, п.5). Найдем   и      Так как

   ,то по формуле (40) находим

   Проведем в интеграле замену переменной, полагая

   тогда

   Следовательно,

   Но

   [См. формулу (29)]. Далее, так как функция   нечетная, то по свойству нечетных функций

   Следовательно,       Дисперсию находим по формуле (45)

   (вычисление интеграла не приводим).     Итак,

   Таким образом, параметры a и   для нормально распределенной случайной величины имеют простой вероятностный смысл: a есть математическое ожидание,   - среднее квадратическое отклонение.