11. Производная функции, заданной параметрически
Пусть функции
и
определены в некоторой окрестности
точки
.
Если функция
непрерывна и строго монотонна на этом
промежутке, то существует обратная
функция
.
Областью определения обратной функции
является множество значений функции
.
Тогда определена сложная функция
,
где
.
Если функции
и
дифференцируемы в точке
,
то сложная функция
дифференцируема в точке
и справедливо равенство
.
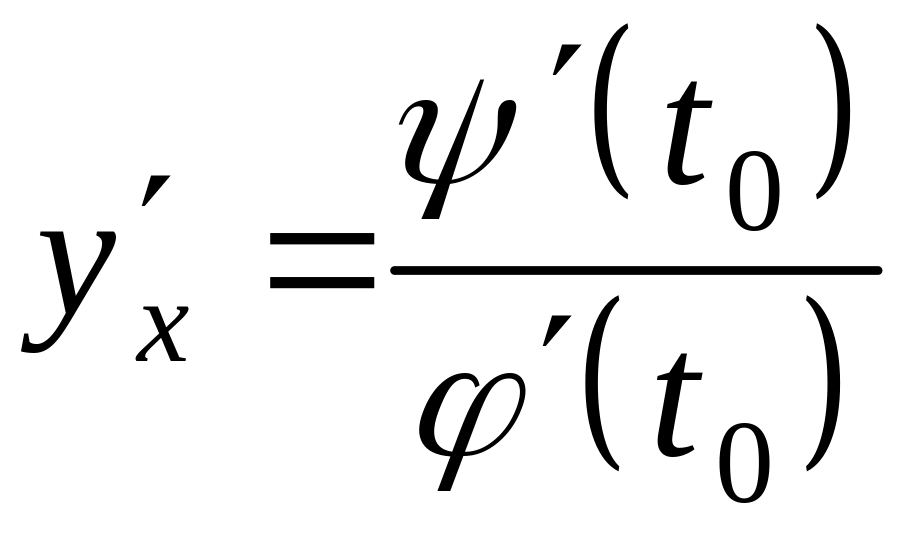или
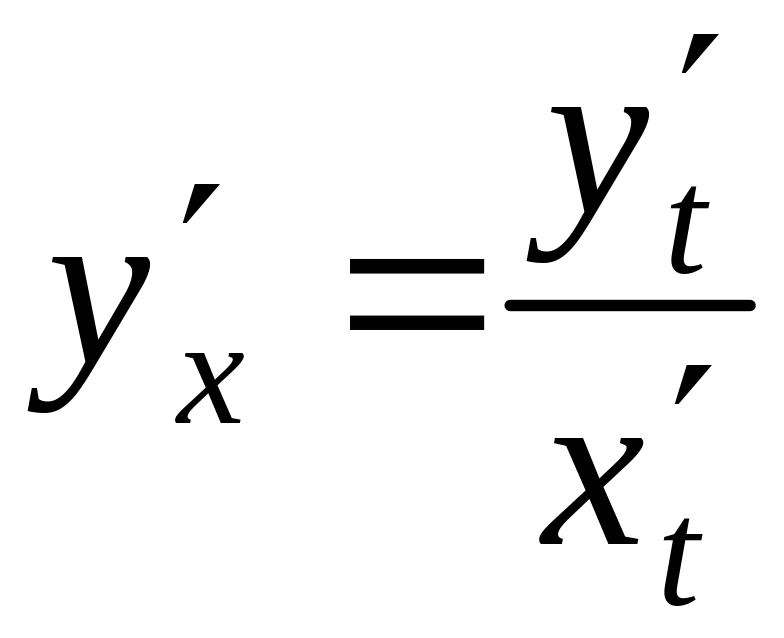
Если функции
и
дифференцируемы в каждой точке окрестности
,
то
|
|
или |
. |
|
как в случае, когда – независимая переменная, так и в случае, когда является функцией какой либо переменной.
12. Производная функции, заданной неявно
Если дифференцируемая
функция
задано неявно уравнением
,
то дифференцируя тождество
как сложную функцию,
можно найти производную
.
В качестве примера
вычислим производную неявной функции
,
задаваемой уравнение
.
В данном конкретном случае существование
такой функции не вызывает сомнения,
например это
.
Продифференцируем уравнение
:
.
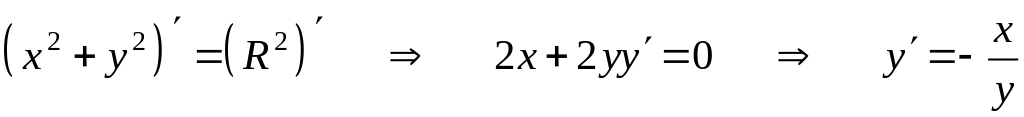Найдем производную функции :
.
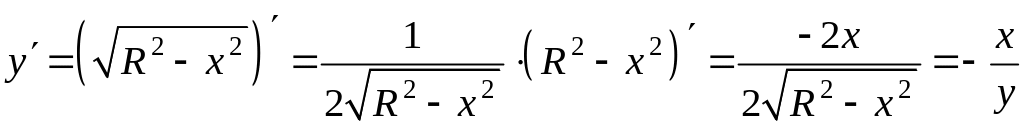В обоих случаях получены одинаковые результаты.
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
(15) |