Лекция № 5

Задачи, приводящие к понятию производной. Геометрический и физический смысл производной. Определение производной. Касательная, нормаль, отрезок касательной, отрезок нормали, подкасательная, поднормаль. Односторонние производные. Бесконечные производные. Дифференциал функции. Правила дифференцирования. Производные суммы, разности, произведения и частного двух функций. Производная обратной функции. Производная сложной функции. Инвариантность формы первого дифференциала. Вычисление производных простейших элементарных функций. Производная функции, заданной параметрически. Производная функции, заданной неявно.

1. Задачи, приводящие к понятию производной

Понятие производной функции в данной точке связано с понятиями касательной к графику функции в этой точке, мгновенной скорости и мгновенного ускорения движения материальной точки, мгновенной силой электрического тока, линейной плотностью стержня.

1.1. Геометрический смысл производной. Приведем определение касательной к графику функции в данной точке.

Пусть функция определена в некоторой окрестности точки и непрерывна в этой точке. Через обозначим приращение аргумента. Будем предполагать, что точка принадлежит данной окрестности . Приращение функции, соответствующее приращению аргумента , обозначим :

.

Рассмотрим секущую (рис. 1), где

, , .

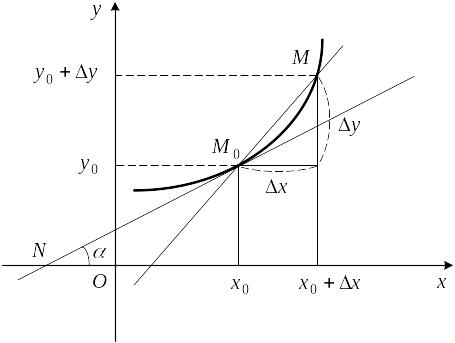
Рис. 1

Она записывается уравнением

,

где – угловой коэффициент – определяется равенством

.

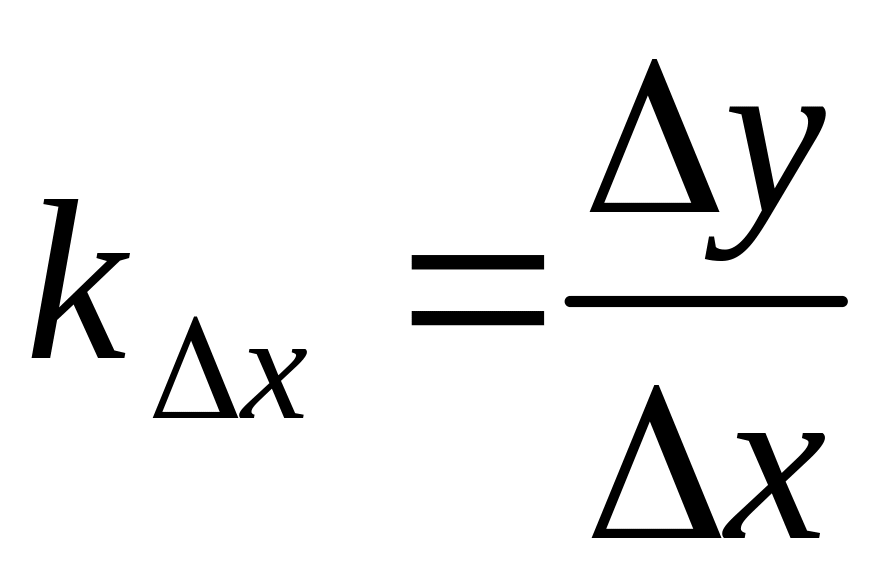Из непрерывности функции следует, что при следует соотношение . Это означает, что точка стремится вдоль графика функции к точке , так как

при .

Если существует предельное положение секущей при (то есть прямая ), то его назовем касательной к графику функции в точке . Существование предельного положения секущей при эквивалентно существованию предела

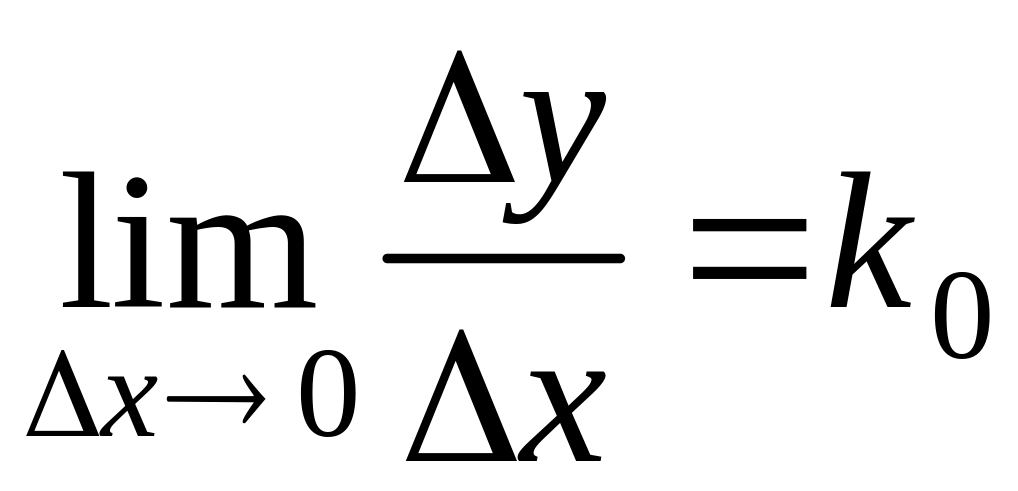. (1)

Таким образом, если существует предел (1), то прямая, проходящая через точку с угловым коэффициентом , является касательной к графику функции в точке .

1.2. Скорость материальной точки. Пусть материальная точка движется по прямой и – ее закон движения ( – путь, пройденный точкой за время от начала движения. За промежуток времени от до точка пройдет путь длины . Поэтому средняя скорость за этот промежуток времени равна

.

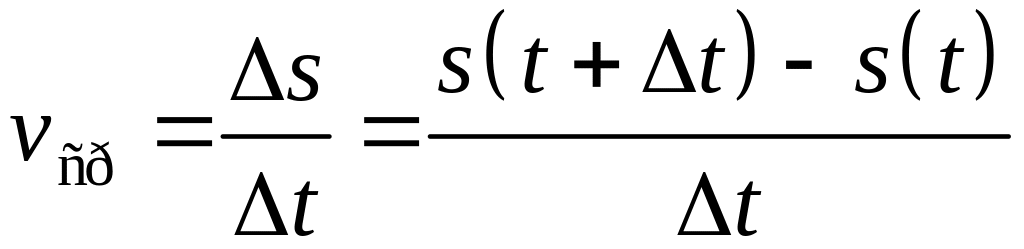Если рассматриваемое движение не является равномерным, то средняя скорость при фиксированном будет меняться при изменении , и чем меньше , тем лучше средняя скорость будет характеризовать движение точки в момент времени .

Скоростью материальной точки в момент времени (мгновенной скоростью) называется предел средней скорости , когда . Таким образом, мгновенная скорость материальной точки в момент времени определяется равенством

.

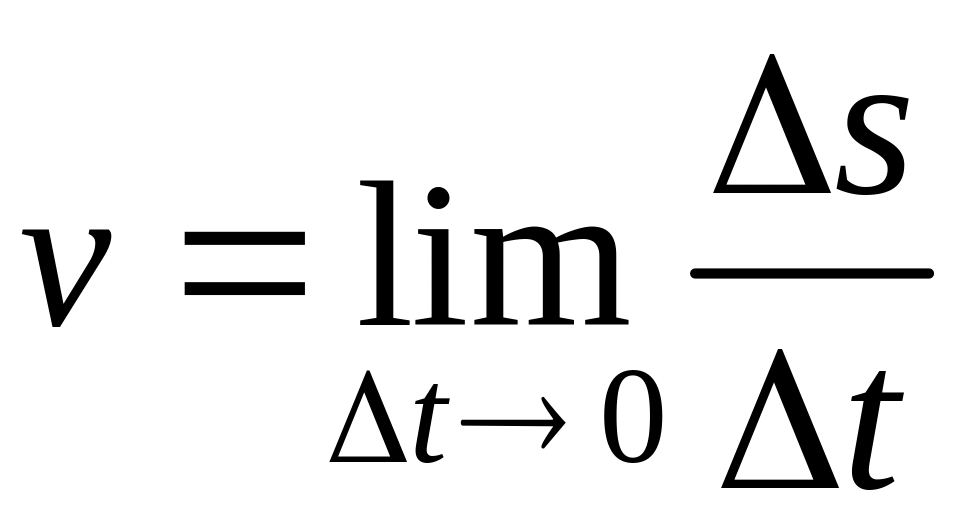1.3. Сила тока в данный момент времени. Пусть – количество электричества, – данное время, – некоторый промежуток времени, протекающее через поперечное сечение проводника, – количество электричества, протекающее через указанное сечение за промежуток времени от момента до момента . Средней силой тока за промежуток времени называется отношение количества электричества, протекающее через указанное сечение за промежуток времени к данному промежутку времени:

.

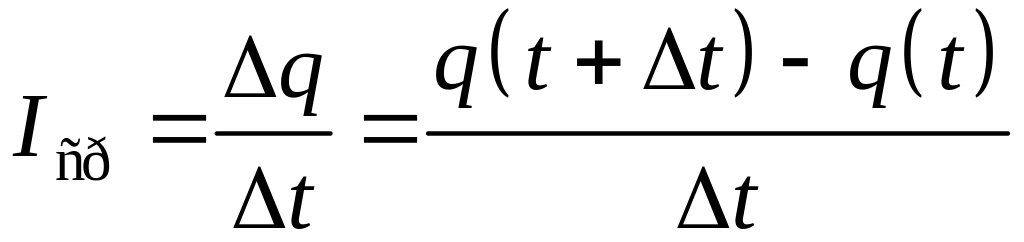Силой тока в данный момент времени (мгновенной силой тока) называется предел средней силой тока , когда . Таким образом, мгновенная сила тока в момент времени определяется равенством

.

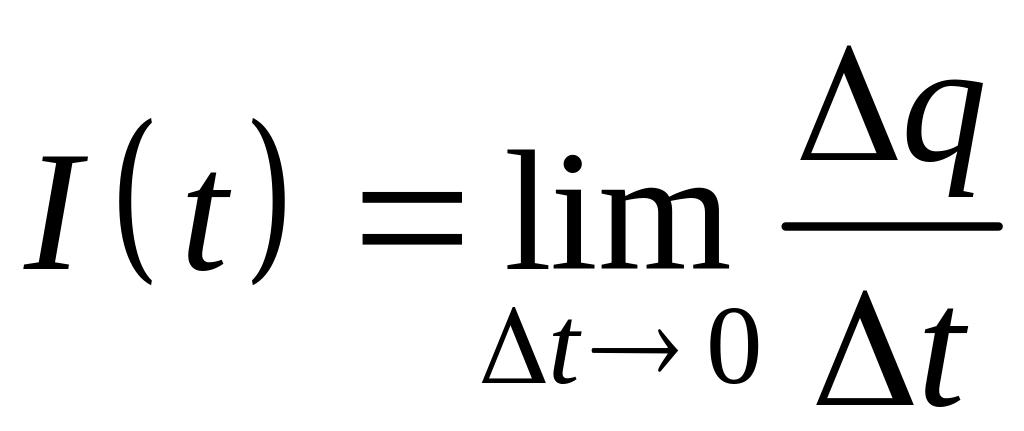1.4. Линейная плотность неоднородного стержня. Стержень называется однородным, если два любых его участка одинаковой длины имеют одинаковую массу, и неоднородным, если участки одинаковой длины имеют разные массы.

Пусть дан неоднородный стержень длины . Через обозначим массу участка стержня длины , отмеряемой от одного фиксированного конца (рис. 2). Масса части стержня, ограниченной точками, расположенными соответственно на расстоянии и

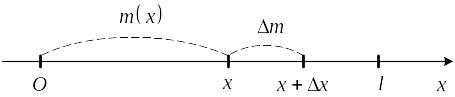
Рис. 2

от указанного конца обозначим

.

Отношение массы части стержня к длине части назовем средней линейной плотностью на указанном участке и обозначим :

.

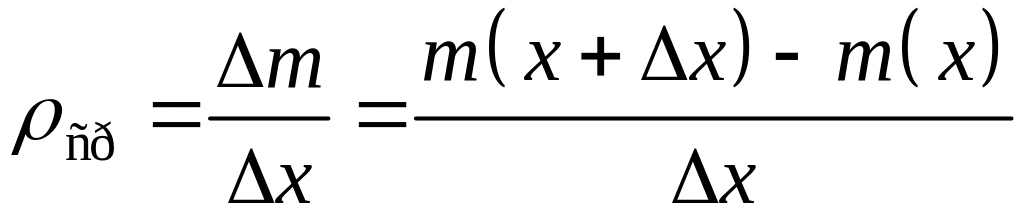Предел средней линейной плотности , когда длина участка стремиться к нулю, назовем линейной плотностью стержня в данной точке и обозначается :

.

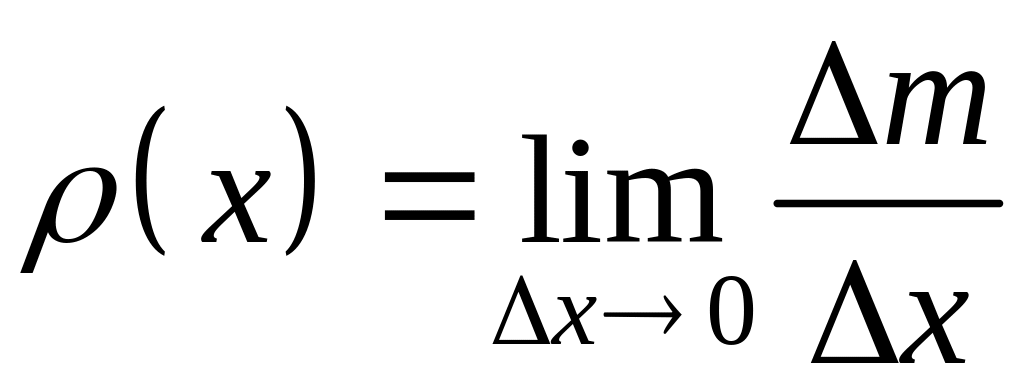Рассмотренные задачи, в которых речь идет о пределе отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, привели к появлению понятия производной функции – одного из важнейших понятий математики.