8. Производная сложной функции

Пусть функция дифференцируема в точке , а функция дифференцируема в точке . Тогда сложная функция дифференцируема в точке и справедливо равенство

.

Если функция дифференцируема в каждой точке промежутка , а функция дифференцируема в каждой точке , то сложная функция дифференцируема в каждой точке и справедливо равенство

.

Правило дифференцирования сложной функции обычно записывается в виде

.

Опуская аргумент и используя другие обозначения производной правило дифференцирования сложной функции можно записать так:

или .

9. Инвариантность формы первого дифференциала

Дифференциал функции имеет один и тот же вид

(12)

как в случае, когда – независимая переменная, так и в случае, когда – дифференцируемая функция какой-либо другой переменной, то есть, .

Действительно, если – дифференцируемая функция переменной , то . По правилу дифференцирования сложной функции

,

откуда по определению дифференциала

.

Так как , то

,

то есть формула (12) остается справедливой при замене на . Это свойство называется инвариантностью формы первого дифференциала.

10. Вычисления производных простейших элементарных функций

Вычисления производных следующих функций выполним исходя из определения производной.

10.1. Производная постоянной функции. Пусть – произвольное вещественное число. Тогда

.

(13)

Пусть – приращение аргумента. Тогда , и поэтому . Равенство (13) доказано.

10.2. Производная степенной функции. Пусть – произвольное вещественное число. Тогда

.

(14)

Покажем справедливость этого равенства исходя из определения производной.

Пусть – приращение аргумента. Тогда . Преобразуем эту разность:

.

Используя табличный предел

,

найдем предел отношения при :

.

Равенство (14) доказано.

10.3. Производная показательной функции. Пусть : , . Тогда

.

(15)

Представим приращение функции в виде:

.

Используя табличный предел

,

найдем предел отношения при :

.

Равенство (15) доказано.

Если , то . Поэтому, из (15), получим

.

(16)

10.4. Производная логарифмической функции. Пусть : , . Тогда

.

(17)

Имеем:

.

Используя табличный предел

,

найдем предел отношения при :

.

Равенство (17) доказано.

В частности, при , из (17), получим

.

(18)

10.5. Производная тригонометрических функций и . Покажем, что

,

(19)

.

(20)

Действительно, так как

,

то используя табличный предел

, (21)

найдем предел отношения при :

.

Равенство (19) доказано.

Так как

,

то используя табличный предел (21), будем иметь

.

Равенство (20) доказано.

Вычисления производных следующих функций основаны на правила дифференцирования.

10.6. Производная тригонометрических функций и . Покажем, что

,

(22)

.

(23)

Действительно, используя правило дифференцирования частного и производные функций и , получим

;

.

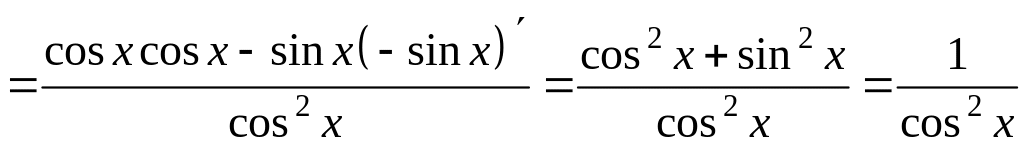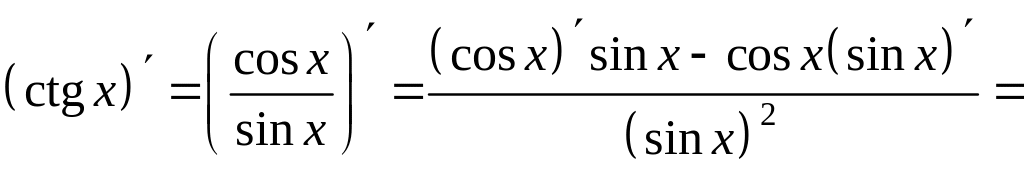
Равенства (22) и (23) доказаны.

10.7. Производная обратных тригонометрических функций. Покажем, что

,

(24)

,

(25)

,

(26)

.

(27)

Если , то

. (28)

Вычислим производную функции (28), используя правило дифференцирования сложной функции:

. (29)

Так как

,

то из (29) вытекает справедливость равенства (24).

Если , то

. (30)

Вычислим производную функции (30), используя правило дифференцирования сложной функции:

. (31)

Так как

,

то из (31) вытекает справедливость равенства (25).

Если , то

. (32)

Вычислим производную функции (32), используя правило дифференцирования сложной функции:

. (33)

Так как

,

то из (33) вытекает справедливость равенства (26).

Если , то

. (34)

Вычислим производную функции (34), используя правило дифференцирования сложной функции:

. (35)

Так как

,

то из (35) вытекает справедливость равенства (27).

Равенства (24) – (27) доказаны.

10.8. Производная гиперболических функций. Покажем, что

,

(36)

,

(37)

,

(38)

.

(39)

Из определений функций , и производной функции , будем иметь:

;

.

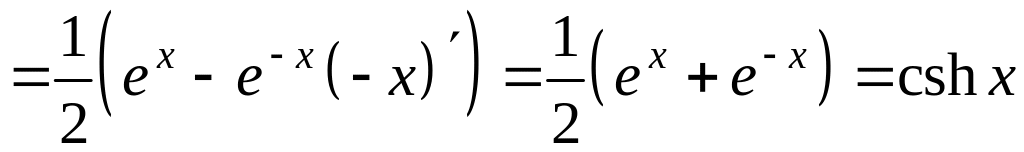Используя вычисленные производные функций , и правило производной частного, получим:

;

.

Равенства (36) – (39) доказаны.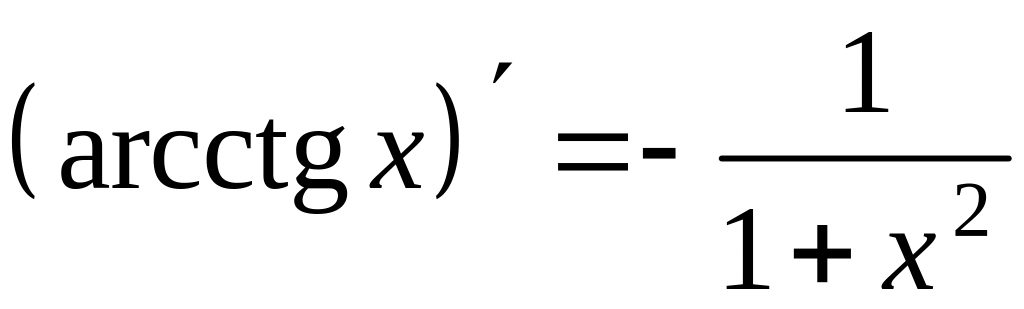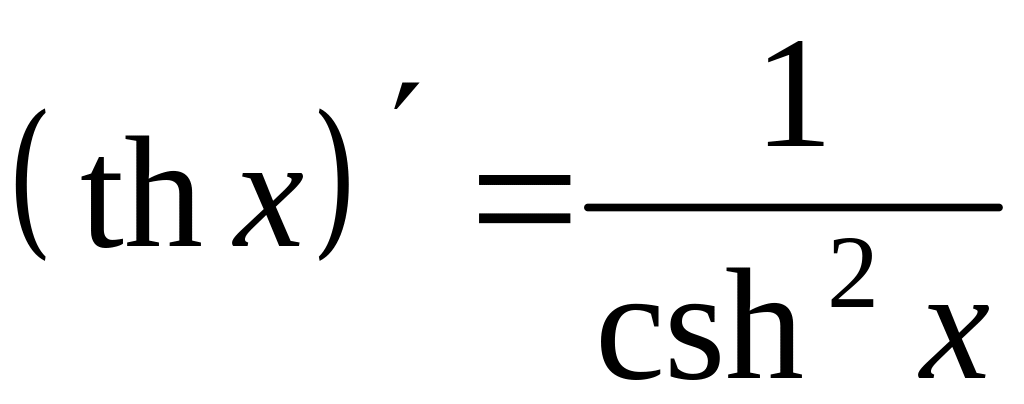