5. Бесконечные производные

Введем в рассмотрение понятие бесконечной производной. Пусть функция определена в некоторой окрестности точки и непрерывна в самой точке .

Если

,

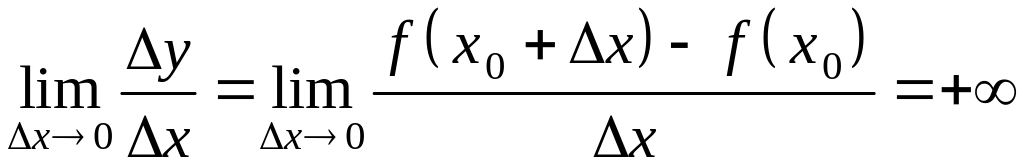то будем говорить, что функция имеет в точке производную, равную , и будем писать

. (4)

В этом случае и .

Если

,

то будем говорить, что функция имеет в точке производную, равную , и будем писать

. (5)

В этом случае и .

Если

,

но не выполняется, ни одно из условий (4) или (5), то будем говорить, что производная не является бесконечностью определенного знака. Например, эта ситуация имеет место, если

и

или

и .

6. Дифференциал функции

Пусть функция определена в некоторой окрестности точки . Функцию назовем дифференцируемой в точке , если ее приращение представимо в виде

, (6)

где не зависит от , а при .

Линейную часть приращению функции (6) назовем дифференциалом функции в точке и обозначим или, короче, :

. (7)

Из соотношений (6) и (7), получим

.

Теорема 1. Для дифференцируемости функции в точке , необходимо и достаточно, чтобы эта функция имела производную в точке и для дифференциала функции справедливо представление

. (8)

Если обозначает приращение функции при приращении аргумента , то дифференциал обозначает приращение касательной к графику этой функции в точке с абсциссой соответствующее тому же приращению аргумента.

Заметим, что дифференциал независимой переменной совпадает с приращением независимой переменной . Действительно, рассматривая функцию для всех точек , имеем . Отсюда и из (8) вытекает равенство

. (9)

Равенства (8) и (9) позволяют представить производную функции как отношение дифференциала функции к дифференциалу независимой переменной

. (10)

Если функция определена в некотором промежутке и в каждой точке имеет производную , то будем говорить, что функция дифференцируема на промежутке . При этом, если промежуток содержит концевые точки, то в них рассматриваются односторонние производные. Равенство (10) для произвольной точки принимает вид

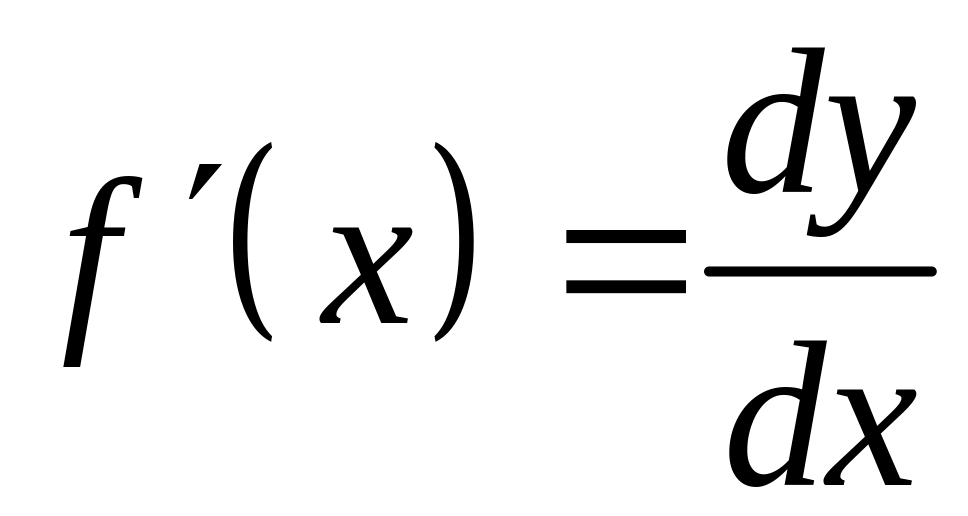или .

7. Правила дифференцирования

Имея некоторый набор дифференцируемых функций можно получить новые дифференцируемые функции с помощью арифметических и алгебраических действий над ними. Получим теперь формулы для производных суммы, разности, произведения, частного двух функций и обратной функции.

7.1. Производная суммы. Пусть функции и определены в некоторой окрестности точки и дифференцируемы в этой точке . Тогда и их сумма дифференцируема в точке и справедливо равенство

.

Полученное равенство следует запомнить, как правило дифференцирования суммы двух функций: производная суммы двух функций равна сумме производных этих функций.

Это правило справедливо и для произвольного конечного числа функций: если функции , ( – произвольное натуральное число) дифференцируемы в точке , то и их сумма дифференцируема в точке и справедливо равенство

.

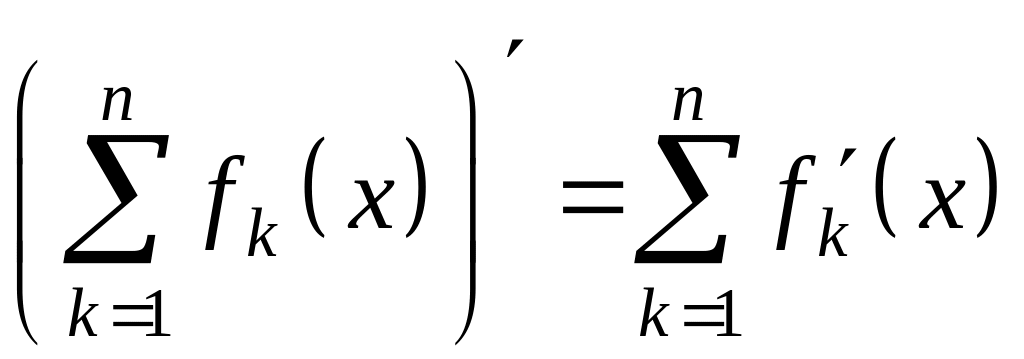7.2. Производная разности. Пусть функции и определены в некоторой окрестности точки и дифференцируемы в этой точке . Тогда и их разность дифференцируема в точке и справедливо равенство

.

Полученное равенство следует запомнить, как правило дифференцирования разности двух функций: производная разности двух функций равна разности производных этих функций.

7.3. Производная произведения. Пусть функции и определены в некоторой окрестности точки и дифференцируемы в этой точке . Тогда и их произведения дифференцируема в точке и справедливо равенство

. (11)

Полученное равенство следует запомнить, как правило дифференцирования произведения двух функций: производная произведения двух функций равна сумме произведений производной каждой из этих функций на другую функцию.

Приведенное правило легко обобщается и для произвольного конечного числа множителей. Например, для трех и четырех множителей равенства, аналогичные (11) имеют вид:

,

.

Производная произведения произвольного количества функций равна сумме произведений производной каждой из этих функций на остальные функции.

7.4. Производная частного. Пусть функции и определены в некоторой окрестности точки и дифференцируемы в этой точке , причем . Тогда и их частное дифференцируемо в точке и справедливо равенство

.

Полученное равенство следует запомнить, как правило дифференцирования частного двух функций: производная частного двух функций равна отношению произведения производной числителя на знаменатель минус произведение числителя на производную знаменателя к квадрату знаменателя.

7.5. Производная обратной функции. Пусть функция непрерывна и строго монотонна в некоторой окрестности точки . Если функция дифференцируема в этой точке и , то функция обратная к функции , дифференцируема в точке , причем

.