2. Определение производной

Пусть функция определена в некоторой окрестности точки и пусть – произвольное достаточно малое приращение аргумента такое, что точка также принадлежит данной окрестности . Если отношение

.

имеет конечный предел при , то этот предел называется производной функции в точке и обозначается :

.

Таким образом, производная функции в точке есть предел отношения функции к приращению аргумента при условии, что , то есть

.

Из этого равенства следует, что

, (2)

где – бесконечно малая величина относительно :

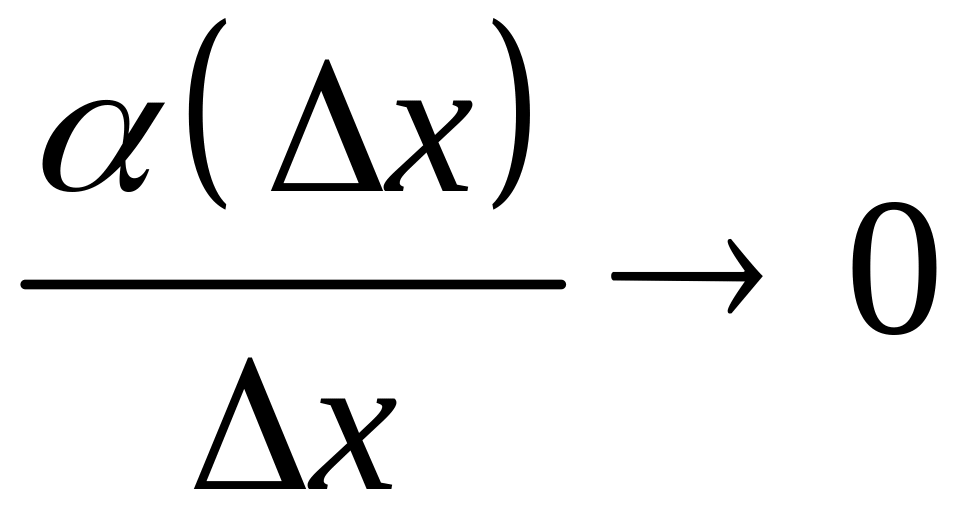при .

Из равенства (2) получаем, что

.

Это означает, что при существовании производной , из соотношения следует выполнение условия . Таким образом, из существования производной следует непрерывность функции в точке , то есть непрерывность функции в данной точке является необходимым условием существования производной этой функции в данной точке.

Операция вычисления производной функции в данной точке называется дифференцированием в данной точке.

3. Касательная, нормаль, отрезок касательной, отрезок нормали, подкасательная, поднормаль

Пусть функция дифференцируема в точке . Уравнение касательной (рис. 3) к графику функции в точке с абсциссой (то же самое в точке ) имеет вид

.

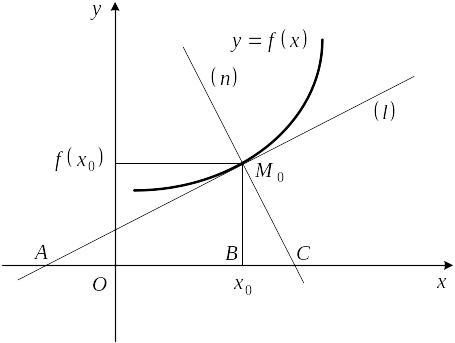
Рис. 3

Проведем через точку прямую , перпендикулярную касательной . Эту прямую назовем нормалью к графику функции в точке с абсциссой (или в точке ).

Пусть – точка пересечения касательной с осью абсцисс, – точка пересечения нормали с осью абсцисс, а – проекция точки на ось абсцисс.

Отрезок называется отрезком касательной, а отрезок – подкасательной.

Отрезок называется отрезком нормали, а отрезок – поднормали.

4. Односторонние производные

Аналогично понятиям односторонних пределов функции вводятся понятия односторонних производных.

Пусть функция определена в правой окрестности точки и пусть – произвольное достаточно малое положительное приращение аргумента такое, что точка также принадлежит данной окрестности . Если существует конечный предел

,

то этот предел называется правой производной функции в точке и обозначается :

.

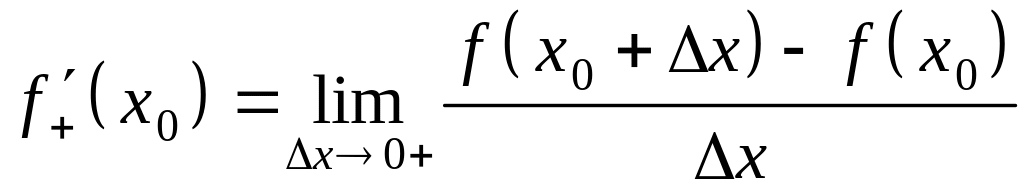Во избежание путаницы отметим, что запись эквивалентна соотношениям и :

.

Пусть функция определена в левой окрестности точки и пусть – произвольное достаточно малое отрицательное приращение аргумента такое, что точка также принадлежит данной окрестности . Если существует конечный предел

,

то этот предел называется левой производной функции в точке и обозначается :

.

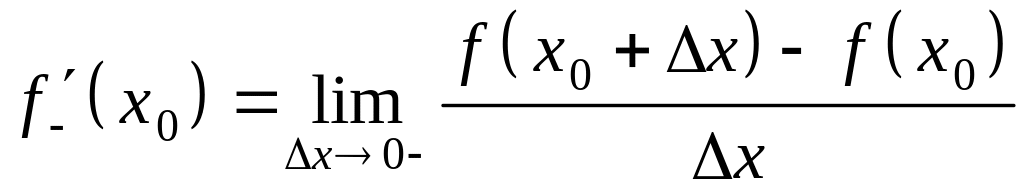Аналогично приведенному выше замечания отметим, что запись эквивалентна соотношениям и :

.

Если функция имеет производную в точке , то она имеет и односторонние производные и в этой точке и справедливы равенства

. (3)

Верно и обратное утверждение: если функция имеет односторонние производные и в этой точке и выполняется условие , то функция имеет производную в этой точке и имеет место равенства (3).