7.3.2. Алгоритм Джарвиса

Данный алгоритм основан на следующем утверждении. Отрезок L, определяемый двумя точками, является ребром выпуклой оболочки тогда и только тогда, когда все другие элементы множества S лежат на L или с одной стороны от него.

Из этого «вытекает» следующая логика: N точек определяет порядка n² отрезков. Для каждого из этих отрезков можно определить положение остальных (N-2) точек относительно него.

Таким образом, за время порядка O(N³) можно найти все пары точек, определяющих ребра выпуклой оболочки. Затем эти точки следует расположить в порядке последовательности вершин оболочки.

Джарвис заметил, что данную идею можно улучшить, если учесть следующий факт. Если установлено, что отрезок q₁q₂ является ребром оболочки, то должно существовать другое ребро с концом в точке q₂, принадлежащее выпуклой оболочке. Уточнение этого факта приводит к алгоритму со временем работы O(N²).

7.3.3. Рекурсивный алгоритм

М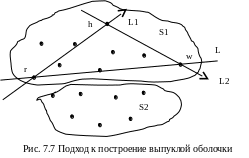 ножество S разделяется на 2 подмножества S1 и S2 примерно равной мощности, каждое из которых будет содержать одну из двух ломаных, соединение которых даст многоугольник выпуклой оболочки (рис. 7.7). Найдем точки w и r, имеющие наибольшую и наименьшую абсциссы соответственно. Проведем через них прямую L, тем самым разобьем множество точек на 2 подмножества – выше и ниже прямой L.

Определим точку h, для которой треугольник (hwr) имеет наибольшую площадь. Точка h гарантированно принадлежит выпуклой оболочке (так как если через h провести прямую, параллельную L, то выше точки h не окажется ни одной точки).

Через точки w и h проведем прямую L1, а через h и r – L2. Для каждой точки множества S1 определяется ее положение относительно этих прямых. Все точки, расположенные справа относительно этих прямых являются внутренними точками треугольника, и поэтому могут быть исключены для дальнейшей обработки.

Никакая из точек не лежит одновременно слева от L1 и слева от L2, следовательно, опять мы получаем 2 отдельных множества. Процесс продолжают до тех пор, пока слева от строящихся прямых типа L1 и L2 есть точки.

Разбиение множества на два подмножества выполняется с трудоёмкостью Θ( ). Нет гарантии того, что после разбиения будут решаться две задачи с трудоёмкостью Θ( ) каждая. Это является следствием того, что 90% точек может оказаться в одном подмножестве, тогда как в другом подмножестве будет находиться лишь 10% всех точек. В среднем случае получим f_a(n)=Θ(nlnn).

7.4. Вопросы для самоконтроля

1. Варианты представления точки на плоскости.

2. Понятие ориентированной площади.

3. Определение выпуклости многоугольника.

4. Построение выпуклой оболочки алгоритмом Грэхема.

5. Построение выпуклой оболочки алгоритмом Джарвиса.

6. Рекурсивный алгоритм построения выпуклой оболочки.

8. Задачи класса np

До сих пор все рассмотренные нами алгоритмы решали поставленные задачи за разумное время. Порядок сложности всех этих алгоритмов был полиномиален. Иногда время их работы оказывалось линейным: при удвоении списка алгоритм работает вдвое дольше. Встречались и алгоритмы сложности N² (сортировка): если длину входного списка удвоить, то время работы алгоритма возрастает в 4 раза. Сложность стандартного алгоритма умножения матриц равна O(N³), и при увеличении размеров матрицы вдвое такой алгоритм работает в 8 раз дольше. Хотя это и значительный рост, его все-таки можно контролировать.

В этом разделе будут рассмотрены задачи, сложность решения которых имеет порядок факториала (O(N!)), или экспоненты O(е^N). Другими словами, для этих задач неизвестен алгоритм их решения за разумное время.

Единственный способ найти разумное или оптимальное решение такой задачи состоит в том, чтобы догадаться до ответа и проверить его правильность.

Ранее рассмотренные алгоритмы относятся к так называемому Р-классу – классу задач полиномиальной сложности, или практически разрешимых.

Более точно задача относится к классу P, если существует алгоритм, правильно решающий эту задачу за время O(n^k), где n – длина входа алгоритма, а k есть константа, не зависящая от n [1]. Реально степень k < 6, и мы можем получить решение задачи из класса P за приемлемое время даже для больших размерностей.

Новый рассматриваемый класс задач образует класс NP – недетерминированной полиномиальной сложности. Сложность всех известных алгоритмов, решающих эти задачи, либо экспоненциальна, либо факториальна. Например, для сложности 2^N при добавлении одного элемента время увеличивается вдвое. Это значительное возрастание времени при небольшом удлинении входа.

Класс NP был так же определен Эдмондсом, как класс задач, для которых возможна проверка полученного решения за время O(n^k) (быстро проверяемые задачи). В 1971 году Кук ввел понятие NP – полных задач, как подкласса в NP – это задачи, к которым за время, полиномиальное относительно длины входа, могут быть сведены любые другие задачи из класса NP.

С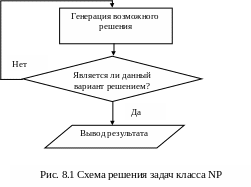 ловосочетание «недетерминированные полиномиальные», характеризующее задачи из NP класса, объясняется следующим двухшаговым подходом к их решению (рис. 8.1). На первом шаге имеется недетерминированный алгоритм, генерирующий возможные решения такой задачи (что-то вроде попытки угадать решение; иногда такая попытка оказывается успешной и мы получаем оптимальный или близкий к оптимальному ответ; иногда – безуспешной и ответ далек от оптимального). На втором шаге проверяется, действительно ли ответ, полученный на первом шаге, является решением исходной задачи.

Каждый из этих шагов по отдельности требует полиномиального времени. Проблема в том, что мы не знаем, сколько раз нам придется повторить оба этих шага, чтобы получить искомое решение.

Хотя оба шага – полиномиальны, число обращений к ним может оказаться экспоненциальным или факториальным.

Практически все задачи, представленные ниже, могут быть сформулированы как оптимизационные, либо как задачи о принятии решения. Целью оптимизационной задачи является конкретный результат, представляющий собой минимальное или максимальное значение. В задаче о принятии решения обычно задается некоторое пограничное значение, и нас интересует, существует ли решение большее или меньшее указанной границы.

Ответом в задачах оптимизации служит конкретный результат, а в задачах о принятии решения – «да» или «нет».

Ясно, что ответ в задаче о принятии решения зависит от выбранной границы – если эта граница очень велика (например, в задаче о коммивояжере она превышает суммарную стоимость всех дорог), то ответ («да») получить не сложно. Если эта граница чересчур мала (меньше стоимости любого пути между городами), то ответ («нет») также дается легко.

В остальных промежуточных случаях время поиска ответ велико и сравнимо со временем решения оптимизационной задачи.