4.3.2. Обход в ширину

При обходе графа по уровням мы, после посещения первого узла, посещаем все соседние с ним вершины. При втором проходе посещаются все вершины «на расстоянии двух ребер» от начальной. При каждом новом проходе обходятся вершины, расстояние до которых от начальной точки на 1 больше предыдущего.

В графе могут быть циклы, поэтому не исключено, что одну и ту же вершину можно соединить с начальной двумя путями. Мы обойдем эту вершину впервые, дойдя до нее по самому короткому пути. Чтобы предупредить повторные посещения, необходимо вести список посещений вершин.

Порядок обхода вершин графа, представленного на рис.4.4, соответственно 1, 2, 5, 3, 4, 8, 9, 6, 7

В основе обхода в глубину лежала стековая структура данных (LIFO), а при обходе по уровням мы воспользуемся очередью (FIFO)

WidthWay (G, v)

// G - граф, заданный некоторым способом

// v – начальная вершина обхода

Visit (v); Mark (v); Queue (v);

While очередь не пуста do

DeQueue (x) // исключаем пройденную вершину из очереди

for (каждого ребра Xw в графе G) do

if (вершина w не помечена)

then visit (w)

Mark (w)

Queue (w)

endif

endfor

endwhile

end

Этот алгоритм заносит в очередь корень дерева обхода по уровням, а затем немедленно удаляет его из очереди. При просмотре соседних с корнем вершин, он заносит их в очередь.

После посещения всех соседних с корнем вершин происходит возвращение к очереди и обращение к первой вершине оттуда.

Поскольку узлы добавляются в конец очереди, ни одна из вершин находящихся на расстоянии двух ребер от корня не будет рассмотрена повторно, пока не будут обработаны и удалены из очереди все вершины на расстоянии одного ребра от корня.

Асимптотическая оценка сложность приведенных алгоритмов – O(N²), где N – количество вершин, или О(М), где М – количество ребер.

С помощью любого из этих методов можно проверить, связен ли рассматриваемый граф. При обходе графа можно составлять список пройденных узлов, а по завершении обхода составленный список можно сравнить со списком всех узлов графа. Если списки содержат одни и те же элементы, то граф связен. В противном случае в графе есть вершины, до которых нельзя дойти из начальной вершины, поэтому он несвязен.

4.4. Поиск остовного дерева минимального веса

Минимальным остовным деревом (MOД) связного взвешенного графа, называется его связный подграф, представляющий собой дерево и состоящий из всех вершин исходного графа и некоторых его ребер, причем сумма весов ребер является минимально возможной (еще говорят – каркас минимального веса).

4.4.1. Алгоритм Дейкстры – Прима

Алгоритм использует для поиска MOД так называемый «жадный» метод. Жадные алгоритмы действуют, используя в каждый момент лишь часть исходных данных и принимая лучшее решение на основе анализа этой части.

Для этой задачи – на каждом шаге рассматривается множество ребер, допускающих присоединение к уже построенной части остовного дерева, и из них выбирается ребро с минимальным весом.

Разобьем вершины графа на 3 класса: вершины, вошедшие в уже построенную часть дерева; вершины, окаймляющие построенную часть, и еще не рассмотренные вершины.

Начнем с произвольной вершины графа и включим ее в остовное дерево (выбор вершин в случае единственного MOД значения не имеет).

Все вершины, связанные с данной, заносим в кайму. Затем выполняется цикл поиска ребра с минимальным весом, соединяющего уже построенную часть остовного дерева с каймой.

Это ребро вместе с новой вершиной добавляется в дерево, и происходит обновление каймы. Работа заканчивается, когда в дерево попадут все вершины.

Общее описание алгоритма:

Выбрать начальный узел.

Сформировать начальную кайму (вершины, соседние с начальным узлом)

While в графе есть вершины, не попавшие в дерево do

выбрать ребро из дерева в кайму с min весом

добавить конец ребра к дереву

изменить кайму (для чего добавить в кайму вершины, соседние с новой)

обновить список ребер из дерева в кайму, так чтобы он состоял из ребер наименьшего веса.

endwhile

Работа данного алгоритма по шагам приведена на рис.4.5.

1 шаг (рис.4.5 б). В кайму заносятся вершины D,C,D,F. Минимальное ребро AB = 2, следовательно, к остову добавляем B.

2 шаг (рис.4.5.в) После добавления B, определяем, не следует ли добавить к кайме новые вершины. Выходим на вершины E и G.

Так как они соединены только с вершиной В уже построенной части дерева, мы добавляем соединяющие ребра к списку, рассматриваемому на следующем шаге.

К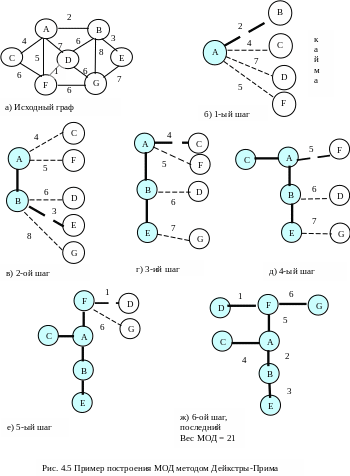 роме того, необходимо проверить, являются ли ребра, ведущие из вершины A в C, D и F - кратчайшими, среди ребер, соединяющих эти вершины с деревом; или есть более удобные ребра из B? В исходном графе B не соединена непосредственно ни с C, ни с F, поэтому для них ничего не меняется. А вот ребро BD короче ребра AD, и поэтому должно его заменить.

Наименьший вес в кайме теперь у ребра BE (3), добавляем к дереву Е (рис.4.5г).

На следующем шаге добавляем вершину С (рис.4.5 д). Следующая вершина МОД – F (рис.4.5 д). Добавление очередных вершин показано на рис.4.5 е) и ж) соответственно.

Такой принцип добавления очередной вершины исключает циклы и образуемый алгоритмом на каждом шаге граф является деревом.

Существует красивое доказательство [1] того, что построенное остовное дерево обладает минимальным весом.