4.4.2. Алгоритм Крускала
В отличие от алгоритма Дейкстры – Прима, алгоритм Крускала (Kruskal) [1,2] делает упор на ребрах графа.
В этом алгоритме начинаем с пустого дерева и добавляем к нему ребра в порядке возрастания их весов, пока не получим набор из ребер, объединяющий все вершины графа.
Если ребра закончатся до того, как все вершины будут соединены между собой, то это означает, что исходный граф был несвязным, и полученный результат есть объединение МОД для всех его компонентов связности.
Пример поиска (тот же граф, что и для алгоритма Дейкстра-Прима, рис.4.5 а) приведен на рис. 4.6.
Выбираем ребро с минимальным весом DF на первом шаге. На втором шаге из оставшихся выбираем ребро АВ. Для всех остальных шагов выбираем ребро с минимальным весом. Добавляемое ребро не должно приводить к образованию циклов. Так, на 6-м шаге с одинаковым весом будут ребра CF, DB, DG, FG. Добавление CF или DB приводит к образованию циклов, поэтому их исключаем из рассмотрения. Добавление DG, FG – равнозначно.
Примерные шаги алгоритма:
1. Отсортировать ребра в порядке возрастания весов, инициализировать структуру разбиений.
2. Начав с первого ребра в перечне, добавлять ребра в граф Q, соблюдая условие: добавление не должно приводить к появлению цикла в Q.
3. Повторять шаг 2, пока число ребер в Q не стане равным N-1. Получившееся дерево является МОД.
4.5. Алгоритм поиска кратчайшего пути
Результатом алгоритма поиска кратчайшего пути является последовательность ребер, соединяющая две заданные вершины и имеющая наименьшую длину среди таких последовательностей.
На первый взгляд кажется, что мы можем воспользоваться алгоритмом построения МОД, чтобы отбросить лишние ребра, а затем взять путь, соединяющий заданные вершины в построенном остовном дереве. Но такое действие не всегда приводит к нужным результатам (рис.4.7). Путь по минимальному остовному дереву из А в В дает 4. При поиске МОД как раз исключается ребро АВ. Следовательно, для поиска кратчайшего пути этот алгоритм надо модифицировать.
М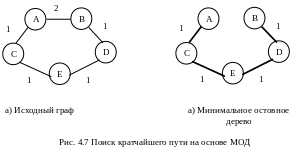
одифицированный
алгоритм выглядит так:
1. выбрать начальную вершину
2. создать начальную кайму из вершины, соединенных с начальной
while вершина назначения не достигнута do
выбрать вершину каймы с кратчайшим расстоянием до начальной;
добавить эту вершину и ведущее в нее ребро к дереву;
изменить кайму путем добавления к ней вершин, соединенных с вновь добавленной;
for всякой вершины каймы do
приписать к ней ребро, соединяющее ее с деревом и завершающее кратчайший путь к начальной вершине
endfor
endwhile
end
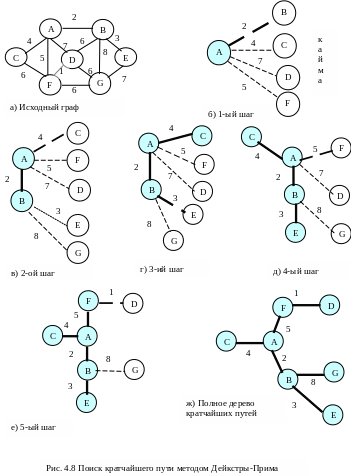
На рис. 4.8 приведен поиск кратчайшего пути из вершины A в вершину G методом Дейкстры-Прима.
На первом шаге (рис.4.8 б) выбираем кратчайшее ребро, выходящее из А – ребро АВ. Далее смотрим, как следует обновить набор путей. С уже построенным деревом соединены теперь вершины E и G, их следует добавить к кайме (рис.4.8 в). Кроме того, мы должны посмотреть на вершину D и сравнить прямой путь из нее в А, длина которого равна 7, и окольный путь через вершину В (длина 8). Прямой путь короче, поэтому приписанное к D ребро менять не следует. Изучив имеющиеся возможности, выбираем кратчайший путь из А в С длины 4. Ребро ВЕ короче (3), но мы рассматриваем полную длину пути из А, а такой путь, ведущий к Е, имеет длину 5. теперь к дереву кратчайший путей добавляется вершина С (рис.4.8 г).
Далее выбираем либо путь из А в Е, либо из А в F, так как оба они имеют длину 5. Пусть алгоритм выбирает вершину с меньшей меткой, то есть Е (рис.4.8 д). Добавление Е не меняет остовных связей, поэтому теперь можно добавить вершину F (рис. 4.8 е).
Путь в вершину D короче пути в G, поэтому в дерево добавляем вершину D. Осталось добавить только вершину G (рис. 4.8 ж). В результате получается дерево кратчайшего пути из А в G, равного 10. Так как вершина G была добавлена последней, то мы получаем полное дерево кратчайших путей. Если бы добрались до нее раньше, то алгоритм тотчас бы завершил свою работу.
