3. Собственные значения и собственные векторы линейного оператора. Матрица оператора в базисе из собственных векторов

Пусть дан линейный оператор 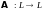( линейное пространство над числовом полем ⁴ ).

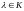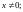Определение 2. Вектор называется собственным вектором, соответствующим собственному значению , если: а) б) 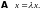Совокупность всех различных собственных значений оператора называют спектром оператора . Обозначение:

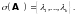
Например, если 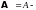матрица 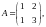то вектор 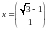является собственным вектором этого оператора, соответствующим собственному значению 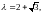так как 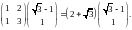При этом

Отметим очевидное свойство собственных векторов: если собственный вектор оператора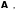 соответствующий собственному значению 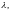то 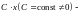тоже собственный вектор оператора соответствующий собственному значению 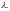В ряде случаев, выбирая постоянную 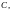можно упростить вид собственных векторов.

Свойства собственных векторов.

1) собственные векторы 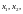соответствующие различным собственным значениям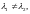 линейно независимы.

2) все собственные векторы оператора , соответствующие одному и тому же собственному значению , образуют линейное подпространство в (его называют собственным пространством оператора отвечающим собственному значению ).

3) В пространстве 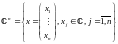любой линейный оператор имеет хотя бы один собственный вектор.

Опишем теперь, как вычисляются собственные векторы и собственные значения. Зафиксируем в пространстве некоторый базис и вычислим матрицу оператора в этом базисе. Тогда операторное уравнение 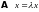(с учетом того, 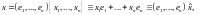где 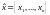) можно записать в матричном виде

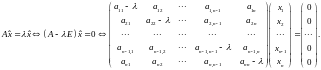
Эта система должна иметь нетривиальное решение 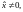поэтому ее определитель должен равняться нулю

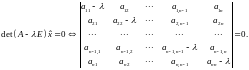
Определитель (5) называется характеристическим определителем матрицы ( или оператора ). Раскрывая его, получим так называемое характеристическое уравнение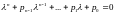 , решая которое, найдем собственные значения матрицы ( или оператора ) . Положив в (4) и решив полученную алгебраическую систему уравнений относительно вектора-столбца 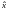, найдем все собственные векторы 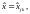соответствующие собственному значению матрицы Затем по формуле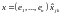 вычислим собственные векторы оператора , соответствующие собственному значению

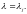
Зачем нужны собственные векторы? Оказывается они обладают следующим важным свойством.

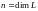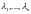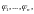Теорема 4. Если оператор имеет в поле различных собственных значений , то собственные векторы соответсвующие этим значениям, образуют базис в Матрица оператора в этом базисе будет диагональной:

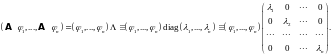
Замечание 2. Оператор называется диагонализируемым ( или оператором простой структуры), если в существует базис, в котором матрица этого оператора диагональна. Из теоремы 4 следует, что оператор , имеющий в в поле различных собственных значений, диагонализируем. Обратное, вообще говоря, не верно: оператор может быть диагонализируемым, не имея различных собственных значений. Например, единичная матрица размерности диагонализируема, но она имеет только одно собственное значение 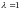кратности В этом случае матрица имеет базис из собственных векторов, но все они отвечают собственному значению

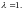
Докажем теперь следующий важный результат.

Теорема 5. Все подобные квадратные матрицы одной и той же размерности имеют одинаковый спектр.

Доказательство. Пусть матрицы и подобны. Тогда существует невырожденная матрица такая что 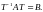Поэтому 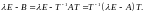Используя теорему об определителе произведения матриц, отсюда получаем, что

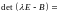
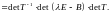Учитывая, что 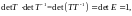получаем отсюда равенство 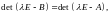которое показывает, что характеристические уравнения матриц и совпадают, поэтому они имею одинаковый спектр. Теорема доказана.

1 Полезно запомнить, что в первый индекс номер строки, а номер столбца, на пересечении которых находится элемент

2 Взаимно однозначное соответствие между двумя множествами, сохраняющее линейные операции между ними, называется линейным изоморфизмом этих множеств.

3 Если оператор линейный, то пишут опуская скобки.

4 В качестве обычно берут множество действительных чисел или множество комплексных чисел

36