
- •1. Векторы. Координаты векторов и линейные операции над векторами
- •2. Скалярное, векторное и смешанное произведение векторов
- •1. Общее уравнение плоскости и уравнение в отрезках
- •2. Особые случаи расположения плоскости в пространстве
- •3. Условия параллельности и перпендикулярности плоскостей. Угол между двумя плоскостями
- •4. Решение различных задач на плоскость
- •5. Нормальное уравнение плоскости. Расстояние от точки до плоскости
- •6. Прямая в пространстве
- •1. Матрицы и действия над ними. Матрицы специального вида
- •2. Определители матрицы и их свойства
- •3. Обратимость матриц. Вычисление обратной матрицы
- •4. Ранг матриц. Теорема о базисном миноре
- •1. Элементарные преобразования и приведение матриц к ступенчатому виду
- •2. Линейные системы алгебраических уравнений. Теорема Кронекера-Капелли
- •3. Линейные пространства и базис. Структура общего решения однородной системы уравнений
- •4. Структура общего решения неоднородной системы уравнений. Алгоритм метода Гаусса построения общего решения линейной алгебраической системы уравнений
- •1. Линейные системы уравнений с квадратной матрицей. Правило Крамера
- •2. Линейный оператор и его матрица в фиксированном базисе. Алгебра линейных операторов и ее связь с алгеброй матриц
- •1.Изменение координат вектора и матрицы оператора при переходе к новому базису
- •2. Ядро и образ линейного оператора
- •3. Собственные значения и собственные векторы линейного оператора. Матрица оператора в базисе из собственных векторов
2. Линейный оператор и его матрица в фиксированном базисе. Алгебра линейных операторов и ее связь с алгеброй матриц
Понятие линейного пространства было введено ранее. Дадим понятие линейного подпространства.
Определение
1. Подмножество
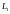 линейного пространства
называется подпространством
пространства
над числовым множеством
,
если наряду с двумя произвольными
элементами
линейного пространства
называется подпространством
пространства
над числовым множеством
,
если наряду с двумя произвольными
элементами
 принадлежащими
принадлежащими
 ему принадлежит и любая линейная
комбинация
ему принадлежит и любая линейная
комбинация
 (
(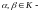 числа).
числа).
Например, пространство двумерных геометрических векторов является подпространством трехмерных геометрических векторов В подпространстве существует свой базис, который можно выбрать из базисных векторов пространства .
Введем
теперь понятие линейного оператора.
Сначала заметим, что любое
отображение
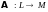 пространства
в пространство
пространства
в пространство
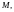 ставящее в соответствие каждому элементу
единственный элемент
ставящее в соответствие каждому элементу
единственный элемент
 по закону
по закону
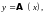 называется оператором (действующим
из пространства
в
пространство
).
называется оператором (действующим
из пространства
в
пространство
).
Определение 2. Оператор называется линейным оператором, если выполняются свойства3:
а)
 б)
б)
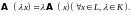
Свойства
а) и б) можно объединить в одно:
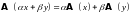

Например,
оператор
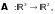 ставящий в соответствие каждому столбцу
ставящий в соответствие каждому столбцу
 столбец
столбец
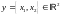 будет линейным оператором, так как
будет линейным оператором, так как

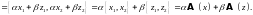
Этот
оператор называется оператором
проектирования.
В качестве другого важного примера
можно указать на оператор, являющийся
матрицей
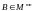 размера
. Этот оператор действует из пространства
размера
. Этот оператор действует из пространства
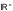 в пространство
в пространство
 Действительно,
Действительно,
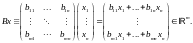
Значит,
оператор
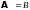 действует из пространства
в пространство
Далее, из определения действий над
матрицами вытекает свойство
действует из пространства
в пространство
Далее, из определения действий над
матрицами вытекает свойство
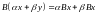 для любых столбцов
для любых столбцов
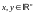 и любых чисел
и любых чисел
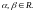 Поэтому матрица
является линейным оператором.
Поэтому матрица
является линейным оператором.
Обозначим
через
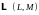 множество всех линейных операторов
множество всех линейных операторов
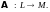 В
этом множестве естественным образом
вводятся линейные операции над
операторами:
В
этом множестве естественным образом
вводятся линейные операции над
операторами:
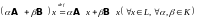
(при
 получаем сумму операторов
получаем сумму операторов
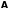 и
и
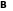 ,
при
,
при
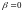 получаем умножение оператора на число).
Нетрудно показать, что пространство
является линейным пространством. Можно
ввести даже операцию умножения операторов
и
получаем умножение оператора на число).
Нетрудно показать, что пространство
является линейным пространством. Можно
ввести даже операцию умножения операторов
и
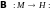
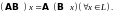
Если
 то в множестве всех линейных операторов
то в множестве всех линейных операторов
 будут определены линейные операции и
операция умножения операторов. Такое
множество называется алгеброй
операторов.
будут определены линейные операции и
операция умножения операторов. Такое
множество называется алгеброй
операторов.
Важным
понятием в линейной алгебре является
понятие матрицы
линейного оператора.
Введем его. Пусть оператор
 является
линейныым и пусть
является
линейныым и пусть
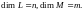 Зафиксируем в пространстве
базис
.
Тогда любой вектор
можно записать в виде
Зафиксируем в пространстве
базис
.
Тогда любой вектор
можно записать в виде
 Точно
так же, если в пространстве
зафиксировать базис
Точно
так же, если в пространстве
зафиксировать базис
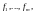 то любой вектор
можно записать в виде
то любой вектор
можно записать в виде

Так
как образы базисных векторов
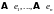 принадлежат пространству
то их можно (согласно (4)) разложить по
базису
принадлежат пространству
то их можно (согласно (4)) разложить по
базису
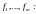

Если
ввести матрицу
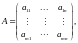 то совокупность последних равенств
можно записать в виде
то совокупность последних равенств
можно записать в виде
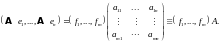
Полученную
таким образом матрицу
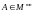 называют матрицей оператора
называют матрицей оператора
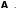 Сформулируем это понятие более точно.
Сформулируем это понятие более точно.
Определение
3. Матрицей
оператора
в
базисе называется матрица
(размера
),
й
столбец которой является координатным
столбцом образа
называется матрица
(размера
),
й
столбец которой является координатным
столбцом образа
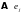 (образа
го
базисного вектора
(образа
го
базисного вектора
 пространства
)
в базисе
пространства
)
в базисе
Пример 3. Пусть пространство является пространством квадратных трехчленов: =
=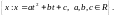 Выберем в нем базис
Выберем в нем базис
 Тогда каждый элемент пространства
можно записать в виде
Тогда каждый элемент пространства
можно записать в виде
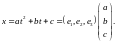
Найдем матрицу
оператора дифференцирования
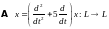 (здесь
(здесь
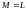 ).
Так как
).
Так как
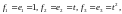 то
то

Следовательно,
матрица
оператора
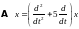 (согласно определению 3) имеет вид
(согласно определению 3) имеет вид
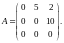
Нетрудно доказать следующее утверждение.
Теорема
2. Если
и
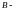 матрицы операторов
матрицы операторов
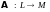 и
и
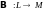 соответственно (в
одном и том же базисе
),
то
матрицами операторов
соответственно (в
одном и том же базисе
),
то
матрицами операторов
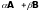
(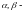 числа)
и
числа)
и
 в том же базисе
будут соответственно матрицы
в том же базисе
будут соответственно матрицы
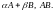
Из
этой теоремы вытекает, что линейные
операции над операторами и операция
умножения операторов можно заменить
на аналогичные операции над их матрицами.
Поэтому, например, вместо того, чтобы
решить операторное уравнение
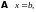 достаточно решить матричное уравнение
достаточно решить матричное уравнение
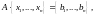 а затем восстановить вектор
а затем восстановить вектор
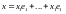 (здесь
(здесь
 матрица
оператора
в базисе
матрица
оператора
в базисе
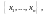
 координатные
столбцы векторов
и
в том же базисе).
координатные
столбцы векторов
и
в том же базисе).
Пример
3. Решить дифференциальное уравнение

Решение. Выбрав в пространстве
квадратных трехчленов
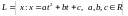 базис
базис
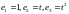 (см.
пример 2), запишем данное дифференциальное
уравнение в матричной форме
(см.
пример 2), запишем данное дифференциальное
уравнение в матричной форме
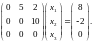
Его решением является вектор-столбец
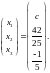
Значит,
решением данного уравнения будет функция
 где
произвольная
постоянная. Заметим, что мы нашли все
решения данного уравнение в пространстве
квадратных трёхчленов. Не исключено,
что оно имеет и другие решения, не
входящие в пространство
.
где
произвольная
постоянная. Заметим, что мы нашли все
решения данного уравнение в пространстве
квадратных трёхчленов. Не исключено,
что оно имеет и другие решения, не
входящие в пространство
.
Пример
4. Даны линейные преобразования в
пространстве
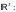

Построить
преобразование
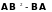 и найти его матрицу в стандартном базисе
и найти его матрицу в стандартном базисе
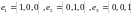 пространства
пространства
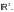
Решение.
Воспользуемся теоремой 2. Если
и
матрицы операторов
и
в базисе
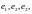 то матрицей оператора
в том же базисе будет матрица
то матрицей оператора
в том же базисе будет матрица
 Построим эту матрицу, а затем восстановим
по ней само преобразование
.
Вычисляя образы базисных векторов для
операторов
и
,
построим их матрицы:
Построим эту матрицу, а затем восстановим
по ней само преобразование
.
Вычисляя образы базисных векторов для
операторов
и
,
построим их матрицы:
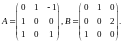
Вычисляем матрицу

Значит,

Лекция 6. Изменение координат вектора и матрицы оператора при переходе к новому базису. Ядро и образ оператора. Собственные значения и собственные векторы линейного оператора. Матрица оператора в базисе из собственных векторов
В предыдущей лекции были определены две алгебры: алгебра линейных операторов и алгебра матриц. Было отмечено, что обе эти алгебры взаимосвязаны между собой и что при решении операторных уравнений можно пользоваться соответствующими им матричными уравнениями. Однако не был затронут вопрос об изменении матрицы оператора и координат вектора при переходе к новому базису. Восполним этот пробел.
