- •1. Обозначения
- •2. Модуль (абсолютная величина) действительного числа
- •3. Понятие функции
- •4. Предел функции
- •5. Бесконечно малые функции и их свойства
- •6. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых
- •7. Бесконечно большие функции и их связь с бесконечно малыми
- •1. Односторонние пределы
- •2. Непрерывность функции в точке
- •3. Производная функции в точке, ее геометрический и механический смысл
- •4. Арифметические действия над производными
- •5. Производная сложной и обратной функций и функции, заданной параметрически
- •6. Производные простейших элементарных функций
- •1. Логарифмическая производная
- •2. Производные и дифференциалы высших порядков
- •3. Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
- •4. Применения формулы Тейлора
- •5. Правило Лопиталя
- •1. Свойства функций, непрерывных на отрезке
- •2. Монотонность функции
- •2. Локальный экстремум
- •3. Выпуклость, вогнутость, точки перегиба
- •4. Исследование функций с помощью высших производных
- •1. Первообразная и неопределенный интеграл
- •2. Замена переменной в неопределенном интеграле
- •3. Интегрирования по частям в неопределенном интеграле
- •4.Выделение полного квадрата
- •5. Определенный интеграл, его свойства и геометрический смысл
- •1. Интеграл с переменным верхним пределом
- •2. Формула Ньютона-Лейбница
- •3. Замена переменных и интегрирование по частям в определенном интеграле
- •4. Интегрирование дробно-рациональных функций
- •4. Интегрирование тригонометрических выражений
 В
каждой лекции все формулы, определения
и теоремы нумеруются так же, как и в
предыдущей лекции, с цифры 1 (т.е. нумерация
не продолжается от лекции к лекции). Это
удобно при чтении лекций.
В
каждой лекции все формулы, определения
и теоремы нумеруются так же, как и в
предыдущей лекции, с цифры 1 (т.е. нумерация
не продолжается от лекции к лекции). Это
удобно при чтении лекций.
Лекция
1. Предел
функции в точке и при
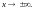 Односторонние пределы. Действия над
пределами. Бесконечно малые функции,
таблица эквивалентных бесконечно малых
и ее применение при вычислении пределов
функций
Односторонние пределы. Действия над
пределами. Бесконечно малые функции,
таблица эквивалентных бесконечно малых
и ее применение при вычислении пределов
функций
1. Обозначения
Множества
(любой природы) обозначаются большими
латинскими буквами
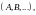 а их элементы – малыми латинскими
буквами
а их элементы – малыми латинскими
буквами
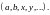 Большими
латинскими буквами обозначаются также
высказывания (например,
Большими
латинскими буквами обозначаются также
высказывания (например,
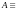 {число
{число
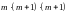 делится на 3}). Везде ниже вводятся
следующие обозначения:
делится на 3}). Везде ниже вводятся
следующие обозначения:
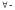 “всякий”,
“каждый”, “ для всякого”,“для каждого”,
“всякий”,
“каждый”, “ для всякого”,“для каждого”,
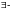 “существует”,
“найдется хотя бы один”,
“существует”,
“найдется хотя бы один”,
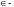 “принадлежит”,
“принадлежит”,
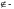 “не принадлежит”,
“не принадлежит”,
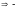 “следует
из”, “вытекает из”,
“следует
из”, “вытекает из”,
 “эквивалентно”,
“необходимо и достаточно”, “тогда и
только тогда”,
“эквивалентно”,
“необходимо и достаточно”, “тогда и
только тогда”,
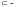 “входит
в”, “содержится в”
“входит
в”, “содержится в”
 или
или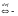 “по
определению” (в тексте слово “если”)
“по
определению” (в тексте слово “если”)
 логическое
“И”,
логическое
“И”,
 логическое “ИЛИ”,
логическое “ИЛИ”,
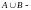 объединение
множеств
объединение
множеств
 и
и

 пересечение множеств
и
пересечение множеств
и
 разность
множеств
и
разность
множеств
и
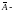 дополнение
(если
дополнение
(если
 высказывание, то
отрицание
высказывания
).
высказывание, то
отрицание
высказывания
).
Через
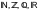 обозначаются множества натуральных,
целых, рациональных и действительных
чисел соответственно
обозначаются множества натуральных,
целых, рациональных и действительных
чисел соответственно
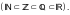
2. Модуль (абсолютная величина) действительного числа
Модуль
числа
определяется следующим образом:
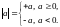
Свойства модуля:
1.
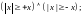 2.
2.
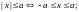 3.
3.
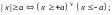
4.
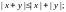 5.
5.
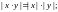 6.
6.
 7.
7.
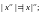
8.

3. Понятие функции
Пусть
даны два множества
и
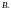
Определение
1. Говорят,
что на множеситве
задана функция
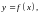 отображающая множество
в множество
отображающая множество
в множество
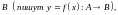 если
каждому элементу
если
каждому элементу
 поставлен в соответствие единственный
элемент
поставлен в соответствие единственный
элемент
 по закону
по закону
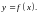 При этом
При этом
 называется аргументом функции
а
называется аргументом функции
а
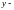 значением этой функции (при указаннном
значении аргумента
).
Множество
называется областью
определения
функции
значением этой функции (при указаннном
значении аргумента
).
Множество
называется областью
определения
функции
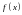 (обозначение:
(обозначение: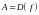 ),
а множество
),
а множество

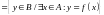 называется множеством
значений этой функции.
называется множеством
значений этой функции.
Чаще
всего функцию задают двумя способами:
а) табличный
способ
(здесь для каждого аргумента
указывается соответствующий
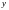 )
и б)
аналитически
(формулой; например
)
и б)
аналитически
(формулой; например
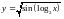 ).
При аналитическом задании функции
).
При аналитическом задании функции
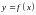 в
качестве области определения обычно
берут естественную
область определения,
т.е. множество
в
качестве области определения обычно
берут естественную
область определения,
т.е. множество
 {
{ выражение
имеет смысл }. Например,
выражение
имеет смысл }. Например,
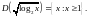 Будет также использоваться обозначение
Будет также использоваться обозначение
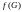 для множества всех значений
для множества всех значений
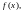 когда
пробегает подмножество
когда
пробегает подмножество
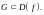
4. Предел функции
Сначала
дадим понятие предела функции в конечной
точке
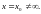 Различают
проколотую
Различают
проколотую
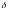 -
окрестность
-
окрестность
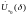 точки
точки
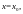 которая определяется как симметричный
интервал
которая определяется как симметричный
интервал
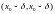 с выброшенной точкой
с выброшенной точкой
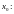

и
просто
-
окрестность
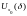 точки
совпадающую с указанным интервалом:
точки
совпадающую с указанным интервалом:

Пусть
функция
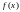 определена в некоторой проколотой
окрестности
определена в некоторой проколотой
окрестности
 точки
точки
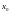 (в самой точке
функция можеть быть определена или нет;
её значение в точке
не существенно).
(в самой точке
функция можеть быть определена или нет;
её значение в точке
не существенно).
Определение
2.
Говорят, что число
P
является пределом функции
в точке
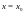 (
или при
(
или при
 если для произвольного числа
если для произвольного числа
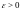 найдется число
найдется число
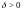 (зависящее, вообще говоря, от
(зависящее, вообще говоря, от
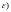 такое, что для всех значений
такое, что для всех значений
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
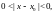 будет иметь место неравенство
будет иметь место неравенство
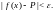 При этом пишут
При этом пишут
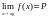 и читают: “ предел функции
при
и читают: “ предел функции
при
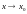 равен
равен
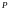 ”.
”.
Это определение записывают кратко так:
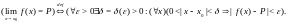
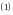
Отметим,
что в этом определении не фигурирует
значение функции
в точке
(
стремится к
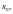 но
но
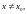 так как
так как
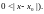 Это означает, что предел
Это означает, что предел
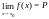 не
зависит от того, каким является значение
функции
в точке
не
зависит от того, каким является значение
функции
в точке
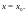 Например, функции
Например, функции
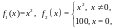
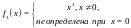
имеют
один и тот же предел
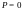 в точке
в точке

Геометрически
высказывание (1) означает, что для любого
существует число
такое, что кривая
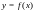 при всех
при всех
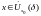 лежит внутри полосы
лежит внутри полосы
 Если эта ситуация будет иметь место для
произвольного интервала
Если эта ситуация будет иметь место для
произвольного интервала
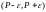 (или, что то же самое, для произвольного
(или, что то же самое, для произвольного
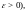 то число
будет пределом функции
при
.
Если же существует интервал
то число
будет пределом функции
при
.
Если же существует интервал
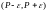 такой, что в любой проколотой окрестности
точки
такой, что в любой проколотой окрестности
точки
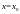 найдется абсцисса
найдется абсцисса
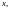 для которой
для которой
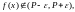 то
то
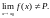 Геометрические соображения часто
используют при доказательстве
существования пределов для конкретных
функций.
Геометрические соображения часто
используют при доказательстве
существования пределов для конкретных
функций.
Теорема
1.
Если существует (конечный) предел
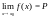 ,
то
он единственен, а сама функция f(x)
является ограниченной при
,
т.е.
,
то
он единственен, а сама функция f(x)
является ограниченной при
,
т.е.
существуют
постоянные
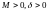 такие, что для
всех
из проколотой окрестности
такие, что для
всех
из проколотой окрестности
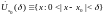 точки
имеет место неравенство
точки
имеет место неравенство
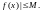
Замечание
1. Если
функция
удовлетворяет условию, записанному
в рамке,
то
ее называют функцией класса
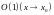 и пишут
и пишут
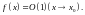 Функции
класса
обладают следующими очевидными
свойствами.
Функции
класса
обладают следующими очевидными
свойствами.
Теорема
2.
Если
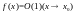 и
и
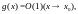 то
то