
- •Экономико-математические методы и модели
- •1. Общие методические рекомендации по изучению дисциплины
- •Библиографический список
- •2. Контрольные задания и методические указания по их выполнению
- •2.1. Контрольные задания
- •Количество зелёной массы, перевозимой с полей, т
- •Уровень выпуска продукции, стоимость сырья, средняя зарплата
- •Использование продукции сельского хозяйства в отраслях региона, тыс. Т
- •Использование продукции лёгкой промышленности в отраслях региона, тыс. Шт.
- •2.2. Методические указания по выполнению контрольной работы №1
- •2.2.1. Методические указания к заданию №1
- •2.2.2. Методические указания к заданию №2
- •2.2.3. Методические указания к заданию №3
- •2.2.4. Методические указания к заданию № 4
- •2.3. Методические указания по выполнению контрольной работы № 2
- •2.3.1. Методические указания к заданию №1
- •2.3.2. Методические указания к заданию № 2
- •2.3.3. Методические указания к заданию № 3
- •2.3.4. Методические указания к заданию № 4
- •Содержание
- •Раздел 1. Общие методические рекомендации по изучению дисциплины …………………3
- •Раздел 2. Контрольные задания и методические указания по их выполнению …………….4
2.2.3. Методические указания к заданию №3
В хозяйстве
необходимо за время уборки при заготовке
силоса перевезти 3600 т зелёной массы с
пяти полей к четырём силосным траншеям.
Зелёная масса каждого поля равна:
![]() =
400,
=
400,
![]() =
500,
=
500,
![]() =
700,
=
700,
![]() =
900,
=
900,
![]() =
1100 т; вместимости силосных траншей
равны:
=
1100 т; вместимости силосных траншей
равны:
![]() =
1200,
=
1200,
![]() =
600,
=
600,
![]() =
800,
=
800,
![]() =
1000 т. Оплата за 1 т зелёной массы,
перевозимую с полей к силосным траншеям,
руб., приведена в табл. 26.
=
1000 т. Оплата за 1 т зелёной массы,
перевозимую с полей к силосным траншеям,
руб., приведена в табл. 26.
Таблица 26
Оплата перевозки зелёной массы с полей в силосные траншеи, руб. за т
Поля |
Силосные траншеи |
|||
1-я |
2-я |
3-я |
4-я |
|
1-е |
5 |
6 |
2 |
2 |
2-е |
9 |
7 |
4 |
6 |
3-е |
7 |
1 |
4 |
5 |
4-е |
5 |
2 |
2 |
4 |
5-е |
6 |
4 |
3 |
4 |
Составить такой план перевозок, чтобы суммарные транспортные затраты были минимальными. Опорный план найти методом наименьшего элемента. Оптимальный план найти методом потенциалов.
Решение.
Предварительно проверим баланс между
общим объёмом зелёной массы
,
вывозимой с полей, и суммарной вместимостью
силосных траншей
![]() .
.
=![]() =
400 + 500 + 700 + 900+1100 = 3600;
=
400 + 500 + 700 + 900+1100 = 3600;
=![]() =1200+600+800+1000
=3600.
=1200+600+800+1000
=3600.
Так как = , то задача является закрытой.
Определим опорный план задачи методом наименьшего элемента.
Среди всех удельных
оплат за перевозку зелёной массы с полей
к силосным траншеям выберем самую
наименьшую. Это оплата перевозки за 1 т
с третьего поля ко второй силосной
траншее
![]() =1.
Будем делать поставку в клетку (3;2).
=1.
Будем делать поставку в клетку (3;2).
1а |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 |
6 – |
2 |
2 |
|
500 |
9 |
7 – |
4 |
6 |
|
700 |
7 |
1 600 |
4 |
5 |
100 |
900 |
5 |
2 – |
2 |
4 |
|
1100 |
6 |
4 – |
3 |
4 |
|
Остатки |
|
0 х |
|
|
|
Определим объём поставки в эту клетку как минимум из остатков объёма зелёной массы третьего поля и вместимости второй силосной траншеи.
Так как зелёная масса ещё не распределялась между полями и траншеями, то остатки равны соответственно значениям объёма зелёной массы третьего поля и вместимости второй силосной траншеи: 700 т и 600 т соответственно. Минимальным будет остаток 600 т.
Поставляем в клетку (3;2) 600 т зелёной массы.
Пересчитываем остатки: с третьего поля осталось перевезти 700 – 600 = 100 т, а остаток вместимости второй силосной траншеи стал равным 600 – 600 = 0. Вычёркиваем из дальнейшего рассмотрения вторую силосную траншею. Как и во втором задании, будем нумеровать таблицы в левом верхнем углу. Выполненные действия отметим в табл. 1а.
Переходим к
следующему шагу метода наименьшего
элемента. Среди всех оплат за перевозку
1 т зелёной массы с полей к силосным
траншеям в оставшейся части таблицы
выбираем наименьшую оплату. Их несколько,
это оплаты перевозки 1 т зелёной массы
с первого поля к третьей и четвёртой
силосным траншеям
![]() =
2,
=
2,
![]() =
2 и оплата перевозки 1 т зелёной массы с
четвёртого поля к третьей силосной
траншее
=
2 и оплата перевозки 1 т зелёной массы с
четвёртого поля к третьей силосной
траншее
![]() =2.
Для поставки зелёной массы выбираем
клетку (1;4).
=2.
Для поставки зелёной массы выбираем
клетку (1;4).
1б |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 |
7 – |
4 |
6 |
|
700 |
7 |
1 600 |
4 |
5 |
100 |
900 |
5 |
2 – |
2 |
4 |
|
1100 |
6 |
4 – |
3 |
4 |
|
Остатки |
|
0 х |
|
600 |
|
Определим объём поставки в эту клетку. Перевозки с первого поля к четвёртой силосной траншее ещё не планировались, тогда остатки зелёной массы для поля и вместимости траншеи равны: для поля – 400 т, для траншеи – 1000 т. Минимальным будет остаток 400 т. Поставляем 400 т зелёной массы в клетку (1;4).
Пересчитываем остатки: для первого поля: 400 – 400 = 0 т, для четвёртой траншеи: 1000 – 400 = 600 т (табл. 1б). Вычёркиваем первое поле из дальнейшего рассмотрения.
Переходим к следующему шагу метода. Опять находим среди всех оплат перевозки 1 т в оставшейся части таблицы наименьшую. Это оплата перевозки = 2. Для поставки выбираем клетку (4;3).
1в |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 |
7 – |
4 – |
6 |
|
700 |
7 |
1 600 |
4 – |
5 |
100 |
900 |
5 |
2 – |
2 800 |
4 |
100 |
1100 |
6 |
4 – |
3 – |
4 |
|
Остатки |
|
0 х |
0 х |
600 |
|
Остатки равны: для поля – 900 т, для траншеи – 800 т. Минимальным будет остаток 800 т. Поставляем 800 т в клетку (4;3).
Пересчитываем остатки: для поля: 900 – 800 = 100 т, для траншеи: 800 – 800 = 0 т (табл. 1в). Третью траншею вычёркиваем из дальнейшего рассмотрения.
Переходим к следующему шагу. Снова находим наименьшую оплату перевозки:
![]() =
4,
=
4,
![]() =
4. Выбираем для поставки клетку (5;4).
=
4. Выбираем для поставки клетку (5;4).
1г |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 |
7 – |
4 – |
6 – |
|
700 |
7 |
1 600 |
4 – |
5 – |
100 |
900 |
5 |
2 – |
2 800 |
4 – |
100 |
1100 |
6 |
4 – |
3 – |
4 600 |
500 |
Остатки |
|
0 х |
0 х |
600, 0 х |
|
Остатки равны: для поля – 1100 т, для траншеи – 600 т. 600 т будет минимальным остатком. Пересчитываем остатки (табл. 1г): для поля 1100 – 600 = 500 т, 600 – 600 = 0 т для траншеи. Вычёркиваем четвёртую траншею.
Следующий шаг
метода. Наименьшая удельная оплата
перевозки
![]() =
5. Выбираем для поставки клетку (4;1).
=
5. Выбираем для поставки клетку (4;1).
1д |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 |
7 – |
4 – |
6 – |
|
700 |
7 |
1 600 |
4 – |
5 – |
100 |
900 |
5 100 |
2 – |
2 800 |
4 – |
100, 0 х |
1100 |
6 |
4 – |
3 – |
4 600 |
500 |
Остатки |
1100 |
0 х |
0 х |
600, 0 х |
|
Смотрим остатки: у четвёртого поля –100 т, для первой траншеи – 1200 т. Остаток 100 т будет минимальным. Делаем поставку в клетку (4;1) в объёме100 т.
Пересчитываем остатки: для поля 100 – 100 = 0 т, для траншеи 1200 – 100 =1100 т (табл. 1д). Четвёртое поле вычёркиваем из дальнейшего рассмотрения.
Переходим к
следующему шагу. Наименьшая оплата
перевозки
![]() =
6. Выбираем клетку (5;1).
=
6. Выбираем клетку (5;1).
1е |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 |
7 – |
4 – |
6 – |
|
700 |
7 |
1 600 |
4 – |
5 – |
100 |
900 |
5 100 |
2 – |
2 800 |
4 – |
100, 0 х |
1100 |
6 500 |
4 – |
3 – |
4 600 |
500, 0 х |
Остатки |
1100, 600 |
0 х |
0 х |
600, 0 х |
|
Остатки равны: поле – 500 т, траншея – 1100 т. Минимальным будет остаток 500 т. Поставляем в клетку (5;1) 500 т. Остатки: 500 – 500 = 0 т для поля, 1100–500=600 т для траншеи (табл. 1е). Пятое поле вычёркиваем.
Следующий шаг
метода. Наименьшая оплата
![]() =7.
Выбираем клетку (3;1).
=7.
Выбираем клетку (3;1).
1ж |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 |
7 – |
4 – |
6 – |
|
700 |
7 100 |
1 600 |
4 – |
5 – |
100, 0 х |
900 |
5 100 |
2 – |
2 800 |
4 – |
100, 0 х |
1100 |
6 500 |
4 – |
3 – |
4 600 |
500, 0 х |
Остатки |
1100, 600, 500 |
0 х |
0 х |
600, 0 х |
|
Остатки: поле – 100 , траншея – 600 т. Минимальный остаток 100 т. Поставляем 100 т в клетку (3;1). Пересчитываем остатки: 100 т для поля, для траншеи 100–100 =500 т
(табл. 1ж). Вычёркиваем третье поле.
Осталась последняя клетка, которая не заполнялась, это клетка (2;1).
1з |
1200 |
600 |
800 |
1000 |
Остатки |
400 |
5 – |
6 – |
2 – |
2 400 |
0 х |
500 |
9 500 |
7 – |
4 – |
6 – |
0 х |
700 |
7 100 |
1 600 |
4 – |
5 – |
100, 0 х |
900 |
5 100 |
2 – |
2 800 |
4 – |
100, 0 х |
1100 |
6 500 |
4 – |
3 – |
4 600 |
500, 0 х |
Остатки |
1100, 600,500, 0 х |
0 х |
0 х |
600, 0 х |
|
Проверяем баланс остатков: для поля остаток – 500 т, для траншеи – 500 т. Баланс есть. Поставляем в клетку (2;1) 500 т. Вычёркиваем из рассмотрения и поле, и траншею (табл. 1з).
Мы получили опорный план, построенный методом наименьшего элемента (табл. 1).
1 |
1200 |
600 |
800 |
1000 |
400 |
5 |
6 |
2 |
2 400 |
500 |
9 500 |
7 |
4 |
6 |
700 |
7 100 |
1 600 |
4 |
5 |
900 |
5 100 |
2 |
2 800 |
4 |
1100 |
6 500 |
4 |
3 |
4 600 |
Будем искать оптимальный план. Для этого применим метод потенциалов.
Методом потенциалов оптимальный план будем находить пошагово. На каждом шаге метода осуществляем переход от одного опорного плана к другому, выполняя следующие действия:
1. Вычислим потенциалы полей и силосных траншей.
2. Вычислим косвенные издержки для свободных клеток.
3. Проверим признак оптимальности плана.
4. Одну из свободных клеток выбираем для перераспределения зелённой массы.
5. Для выбранной клетки строим цикл перераспределения зелёной массы.
6. Пометим клетки цикла знаками «+» и «–».
7. Определим объём перераспределения зелёной массы.
8. Строим новый опорный план.
1) Вычислим потенциалы полей и силосных траншей по заполненным и условно заполненным клеткам.
Произвольно задаём значение одного из потенциалов, например, положим значение потенциала для первого поля равным нулю.
2а |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
|
700 |
7 100 |
1 600 |
4 |
5 |
|
900 |
5 100 |
2 |
2 800 |
4 |
|
1100 |
6 500 |
4 |
3 |
4 600 |
|
|
|
|
|
2 |
|
Рассмотрим первую строку (табл. 2а). В ней ищем нерассмотренные заполненные и условно заполненные клетки. Такие клетки есть, это клетка (1; 4).
По этой клетке определяем потенциал четвёртой силосной траншеи:
![]() =
=
![]() =
0 + 2 = 2.
=
0 + 2 = 2.
Больше нерассмотренных заполненных и условно заполненных клеток в первой строке нет. Переходим к последнему вычисленному потенциалу, к потенциалу = 2. Это потенциал четвёртой силосной траншеи.
2б |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
|
700 |
7 100 |
1 600 |
4 |
5 |
|
900 |
5 100 |
2 |
2 800 |
4 |
|
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
|
|
|
2 |
|
Рассматриваем
четвёртый столбец (табл. 2б). Находим в
этом столбце нерассмотренные заполненные
и условно заполненные клетки. Такие
клетки есть, это клетка (5; 4). По этой
клетке определяем потенциал пятого
поля:
![]() =
=
![]() =
2 – 4 = –2.
=
2 – 4 = –2.
Больше нерассмотренных заполненных и условно заполненных клеток в четвёртом столбце нет. Переходим к последнему вычисленному потенциалу, к потенциалу = – 2. Это потенциал пятого поля.
2в |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
|
700 |
7 100 |
1 600 |
4 |
5 |
|
900 |
5 100 |
2 |
2 800 |
4 |
|
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
|
|
2 |
|
Рассматриваем
пятую строку (табл. 2в). Находим в этой
строке нерассмотренные заполненные и
условно заполненные клетки. Это клетка
(5; 1). По этой клетке определяем потенциал
первой силосной траншеи:
=
![]() =
–2 + 6 = 4.
=
–2 + 6 = 4.
Больше нерассмотренных заполненных и условно заполненных клеток в пятой строке нет. Переходим к последнему вычисленному потенциалу, к потенциалу = – 2. Это потенциал первой силосной траншеи.
2г |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
|
|
2 |
|
Рассматриваем
первый столбец (табл. 2г). Находим в этом
столбце нерассмотренные
заполненные и условно заполненные
клетки. Это клетки (2; 1), (3; 1) и (4; 1). По
этим клеткам определяем потенциалы
второго, третьего и четвёртого полей:
=
![]() =
4 – 9 = –5,
=
=
4 – 9 = –5,
=
![]() =
4 – 7 = –3,
=
=
4 – 7 = –3,
=
![]() =
4 – 5 = –1.
=
4 – 5 = –1.
Больше нерассмотренных заполненных и условно заполненных клеток в четвёртом столбце нет. Переходим к последним вычисленным потенциалам, к потенциалам = –5,
= –3 и = –1.
2д |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
|
2 |
|
Сначала рассмотрим вторую строку. Находим в этой строке нерассмотренные условно заполненные и заполненные клетки. Таких клеток нет (табл. 2д).
Переходим к следующему вычисленному потенциалу, к потенциалу = – 3. Это потенциал третьего поля.
Рассматриваем
третью строку (табл. 2д). Находим в этой
строке нерассмотренные условно
заполненные и заполненные клетки. Это
клетка (3; 2). По этой клетке определяем
потенциал второй силосной траншеи:
=
![]() =
–3 + 1 = –2. Больше нерассмотренных
заполненных и условно заполненных
клеток в третьей строке нет.
=
–3 + 1 = –2. Больше нерассмотренных
заполненных и условно заполненных
клеток в третьей строке нет.
Переходим к
следующему вычисленному потенциалу, к
потенциалу
=
–1. Это потенциал четвёртого поля.
Рассматриваем четвёртую строку (табл.
2е). В четвёртой строке находим
нерассмотренные заполненные и условно
заполненные клетки. Это клетка (4; 3). По
этой клетке определяем потенциал третьей
силосной траншеи:
=
![]() =
–1 + 2 = 1.
=
–1 + 2 = 1.
2е |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
Больше нерассмотренных заполненных и условно заполненных клеток в четвёртой строке нет.
Переходим к последним вычисленным потенциалам. Это потенциалы = – 2 и
= 1.
2 |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
Сначала рассмотрим второй столбец (табл. 2). Ищем в этом столбце нерассмотренные заполненные и условно заполненные клетки. Таких клеток нет.
Рассмотрим третий столбец (табл. 2). Также в нём ищем нерассмотренные заполненные и условно заполненные клетки. Таких клеток тоже нет.
Мы вычислили все потенциалы. Результаты вычислений представлены таблицей 2.
Переходим к выполнению следующего шага метода потенциалов.
2) Вычислим
косвенные издержки свободных клеток,
которые обозначим
![]() .
.
Косвенные издержки для свободных клеток вычисляем по формуле:
=![]() .
.
![]() =
=![]() =
1 ;
=
1 ;
![]() =
=![]() =
8;
=
8;
![]() =
=![]() =
1;
=
1;
![]() =
=![]() =
4;
=
4;
![]() =
=![]() =
– 2;
=
– 2;
![]() =
=![]() = – 1;
= – 1;
![]() =
=![]() =
0;
=
0;
![]() =
=![]() =
0;
=
0;
![]() =
=![]() =
3;
=
3;
![]() =
=![]() =1;
=1;
![]() =
=![]() = 4;
=
= 4;
=![]() =
0.
=
0.
3) Проверяем
признак оптимальности плана:
если для всех
свободных клеток косвенные издержки
положительные (![]() ),
то опорный план является оптимальным.
),
то опорный план является оптимальным.
План не оптимальный, так как = – 2 < 0 и = – 1 < 0.
4) Выбираем клетку для перераспределения зелёной массы. Это одна из клеток таблицы, для которой косвенные издержки строго отрицательные. Выбираем клетку (2;3).
2ж |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
5) Для выбранной клетки (2;3) строим цикл перераспределения зелёной массы.
Выбранную свободную клетку (2;3) включаем в цикл. Далее рассматриваем строку, содержащую эту клетку. Это вторая строка. Во второй строке ищем заполненные и условно заполненные клетки (табл. 2ж). Такие клетки есть, это клетка (2;1). Так как эта клетка является единственной, то её включаем в цикл (рис. 3а) и переходим к ней.
Рассматриваем столбец, содержащий включённую в цикл клетку (2;1).
Это первый столбец.
В нём находим нерассмотренные заполненные
и условно заполненные клетки. Это клетки
(3;1), (4;1) и (5;1) (табл. 2з). Выбираем любую из
них, например клетку (3;1). Включаем её в
цикл (рис. 3б). Переходим к ней.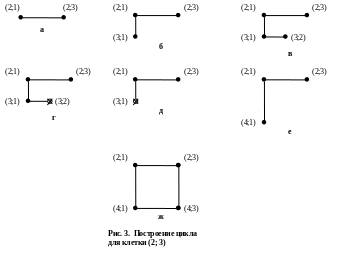
2з |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
Рассматриваем строку, содержащую клетку (3;1). Это третья строка.
2и |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
–5 |
700 |
7 100 |
1 600 |
4 |
5 |
–3 |
900 |
5 100 |
2 |
2 800 |
4 |
–1 |
1100 |
6 500 |
4 |
3 |
4 600 |
–2 |
|
4 |
–2 |
1 |
2 |
|
В третьей строке (табл. 2и) ищем нерассмотренные заполненные и условно заполненные клетки. Такие клетки есть, это клетка (3;2). Так как она единственная, то её включаем в цикл (рис. 3в) и переходим к ней.
2к |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
Рассматриваем столбец, содержащий клетку (3;2). Это второй столбец. В столбце находим нерассмотренные заполненные и условно заполненные клетки. Таких клеток нет (табл. 2к). Вычёркиваем клетку (3;2) из цикла и переходим к предыдущей клетке цикла, к клетке (3;1) (рис. 3г).
Опять рассматриваем третью строку.
2л |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
В третьей строке ищем нерассмотренные заполненные и условно заполненные клетки (табл. 2л). Клетки (3;1) и (3;2) уже рассматривались, других клеток нет.
Вычёркиваем клетку (3;1) из цикла и переходим к предыдущей клетке цикла, к клетке (2;1) (рис. 3д).
Снова рассматриваем первый столбец, содержащий клетку (2;1).
2м |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
– 5 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 100 |
2 |
2 800 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
В столбце находим нерассмотренные заполненные и условно заполненные клетки. Это клетки (4;1) и (5;1), клетки (2;1) и (3;1) уже рассматривались (табл. 2м). Выбираем любую из них, например клетку (4;1). Включаем её в цикл (рис. 3е). Переходим к ней.
2н |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 500 |
7 |
4 × |
6 |
–5 |
700 |
7 100 |
1 600 |
4 |
5 |
–3 |
900 |
5 100 |
2 |
2 800 |
4 |
–1 |
1100 |
6 500 |
4 |
3 |
4 600 |
–2 |
|
4 |
–2 |
1 |
2 |
|
Рассматриваем строку, содержащую клетку (4;1). Это четвёртая строка (табл. 2н).
В этой строке есть заполненная клетка, которая располагается в том же столбце, что и начальная клетка цикла, клетка (2; 3). Это клетка (4; 3). Автоматически её включаем в цикл, и цикл замыкаем (рис. 3е). Построение цикла закончено.
Построенный цикл для свободной клетки (2; 3) изображён на рисунке 3ж.
6) Пометим клетки цикла знаками «+» и «–». Помечать клетки цикла начнём со свободной клетки цикла, клетки (2; 3). Её пометим знаком «+». Далее, двигаясь по циклу в направлении его построения, помечаем остальные клетки цикла, чередуя знаки (рис. 4).
К летку
(2; 1) пометим знаком «–», клетку (4;1) знаком
«+», клетку (4;3) знаком «–». В клетки,
помеченные знаком «+», зелёную массу
будем добавлять, а из клеток, помеченных
знаком «–», зелёную массу будем забирать.
Клетками, откуда зелёная масса забирается,
будут (2;1) и (4;3).
летку
(2; 1) пометим знаком «–», клетку (4;1) знаком
«+», клетку (4;3) знаком «–». В клетки,
помеченные знаком «+», зелёную массу
будем добавлять, а из клеток, помеченных
знаком «–», зелёную массу будем забирать.
Клетками, откуда зелёная масса забирается,
будут (2;1) и (4;3).
7) Определим
объём перераспределения зелёной массы.
Объём перераспределения зелёной массы
![]() равняется наименьшему из объёмов
отрицательных клеток цикла. В клетке
(2; 1) объём поставки зелёной массы
равняется 500 т, а в клетке (4;3) – 800 т (рис.
5). Поэтому объём перераспределения
зелёной массы
равен:
равняется наименьшему из объёмов
отрицательных клеток цикла. В клетке
(2; 1) объём поставки зелёной массы
равняется 500 т, а в клетке (4;3) – 800 т (рис.
5). Поэтому объём перераспределения
зелёной массы
равен:
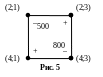 =
=
![]() =
500 т.
=
500 т.
8) Строим
новый опорный план.
Сначала для клеток цикла пересчитываем
объёмы зелёной массы (табл. 3): для клетки
(2; 3) новый объём равен
![]() = 0 + 500 = 500 т, для клетки (2; 1) новый объём
равен
= 0 + 500 = 500 т, для клетки (2; 1) новый объём
равен
![]() =
500 – 500 = 0 т, для клетки (4; 1) новый объём
равен
=
500 – 500 = 0 т, для клетки (4; 1) новый объём
равен
![]() =
100 + 500 = 600 т, для клетки (4; 3) новый объём
равен
=
100 + 500 = 600 т, для клетки (4; 3) новый объём
равен
![]() = 800 – 500 = 300 т. Объём клетки (2; 1) стал
равным нулю, её переводим в ранг свободных,
а клетку (2; 3) переводим в ранг заполненных.
Объёмы остальных клеток таблицы, не
вошедших в цикл, не меняются:
= 800 – 500 = 300 т. Объём клетки (2; 1) стал
равным нулю, её переводим в ранг свободных,
а клетку (2; 3) переводим в ранг заполненных.
Объёмы остальных клеток таблицы, не
вошедших в цикл, не меняются:
![]() = 400,
= 400,
![]() = 100,
= 100,
![]() = 600,
= 600,
![]() = 500,
= 500,
![]() = 600 (табл. 3а). Шаг метода потенциалов
закончен.
= 600 (табл. 3а). Шаг метода потенциалов
закончен.
3а |
1200 |
600 |
800 |
1000 |
400 |
5 |
6 |
2 |
2 400 |
500 |
9 |
7 |
4 500 |
6 |
700 |
7 100 |
1 600 |
4 |
5 |
900 |
5 600 |
2 |
2 300 |
4 |
1100 |
6 500 |
4 |
3 |
4 600 |
Переходим к построенному опорному плану (табл. 3а). Теперь для него применяем метод потенциалов.
1) Вычислим потенциалы полей и силосных траншей (табл. 3).
3 |
1200 |
600 |
800 |
1000 |
|
400 |
5 |
6 |
2 |
2 400 |
0 |
500 |
9 |
7 |
4 500 |
6 |
– 3 |
700 |
7 100 |
1 600 |
4 |
5 |
– 3 |
900 |
5 600 |
2 |
2 300 |
4 |
– 1 |
1100 |
6 500 |
4 |
3 |
4 600 |
– 2 |
|
4 |
– 2 |
1 |
2 |
|
2) Вычислим косвенные издержки для свободных клеток:
=
=
1 ;
=
=
8;
=
=
1;
![]() =
=![]() =
2;
=
2;
=![]() =
6;
=
=
6;
=![]() =1;
=
=
0;
=
=
0;
=1;
=
=
0;
=
=
0;
= = 3; = =1; = = 4; = = 0.
3) Проверим признак оптимальности плана.
План оптимальный, так как для всех свободных клеток косвенные издержки больше либо равны нулю ( ).
По таблице 3 выписываем оптимальный план:
X*
=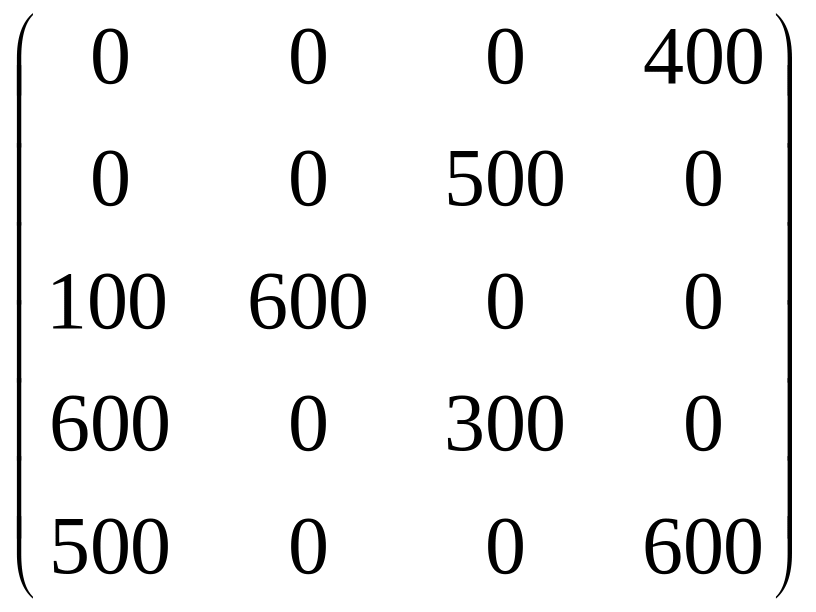 .
.
Для оптимального плана рассчитываем суммарные транспортные издержки:
= 2∙400 + 4∙500 + 7∙100 + 1∙600 + 5∙600+ 2∙300 + 6∙500 + 4∙600 = 13100.
Выписываем ответ: X* = ; =13100.
