Векторы. Основные определения. Проекция вектора на оси.

Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Длиной (модулем) вектора называется расстояние между началом и концом вектора.

Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору. Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.

Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.

Свойства векторов

1) + = + - коммутативность

2) + ( + ) = ( + )+

3) + =

4) +(-1) =

5) () = ( ) – ассоциативность

6) (+) =  +  - дистрибутивность

7) ( + ) =  + 

8) 1 =

Для определения положения произвольной точки могут использоваться различные системы координат. Положение произвольной точки в какой-либо системе координат должно однозначно определяться. Понятие системы координат представляет собой совокупность точки начала отсчета (начала координат) и некоторого базиса. Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.

Если заданы точки А(x₁, y₁, z₁), B(x₂, y₂, z₂), то = (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то .

Свойства проекции:

Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью:

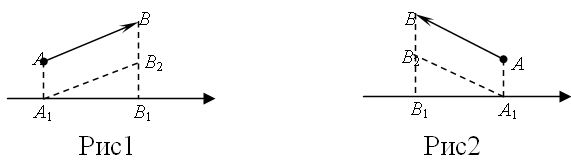
При умножении вектора на число его проекция на ось также умножается на это число.

Проекция суммы векторов на ось равна сумме проекций слагаемых:

Скалярное произведение векторов.

Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

 = | || |cos

Если векторы заданы в координатной форме , ,

то их скалярное произведение вычисляется по формуле:

Свойства скалярного произведения:

1.  = | |²;

2.  = 0, если  или = 0 или = 0.

3.  =  ;

4. ( + ) =  +  ;

5. (m ) = (m ) = m(  );

10. Угол между векторами. Условие параллельности и ортогональности векторов.

Пусть , =>

=> .

Таким образом,  <=> .

Из формулы косинуса угла между векторами легко найти углы , , , которые вектор образует с осями координат. Эти углы называются направляющими углами.

Имеем:

,

,

.

, , называются направляющими косинусами вектора . Они связаны соотношением

.

Следовательно, вектор есть координаты вектора , т.е. вектора и .

.

Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.

Пусть  => => => .

10. Векторное произведение векторов.

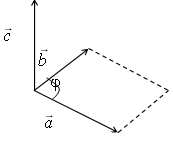
Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:

1) , где  - угол между векторами и ,

2) вектор ортогонален векторам и

3) , и образуют правую тройку векторов.

Обозначается: или .

Свойства векторного произведения векторов

1) ;

2) , если || или = 0 или = 0;

3) (m ) = (m ) = m(  );

4) ( + ) =  +  ;

5) Если заданы векторы в декартовой прямоугольной системе координат с единичными векторами , то

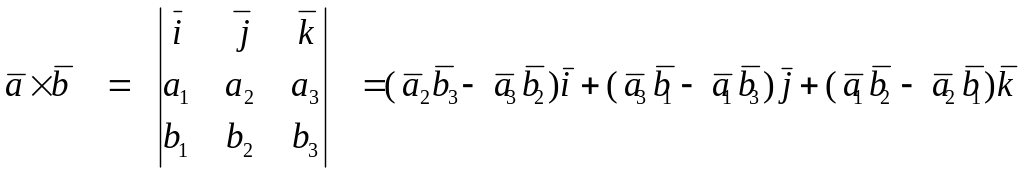
-орты осей координат Ox, Oy, Oz, соответственно:

6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и : .

Замечание: если требуется вычесть площадь параллелограмма, то нужно посчитать сначала ,

затем =

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Смешанным произведением трех векторов

называется число

Смешанное произведение обладает следующими свойствами:

1) , если все три вектора параллельны одной и той же плоскости (компланарны);

2) циклическая перестановка

4) объем параллелепипеда, построенного на векторах и , равен

если a*b*c>0, то тройка a,b,c – правая, если a*b*c<0, то тройка a,b,c - левая

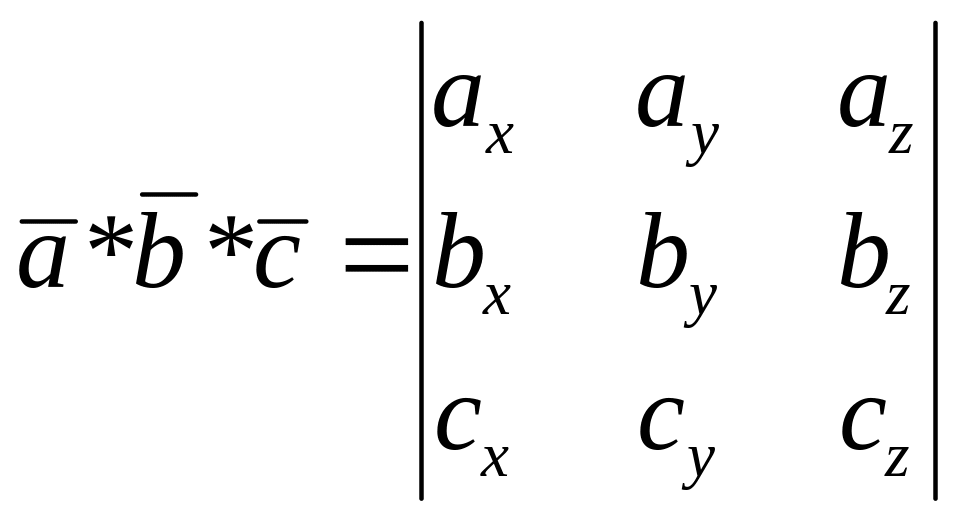
Замечание =0

15. Линейная зависимость векторов.

Векторы называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно _i , т.е. .

Если же только при _i = 0 выполняется , то векторы называются линейно независимыми.

Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Свойство 6. Любые 4 вектора линейно зависимы.

22. Линейно зависимые и линейно независимые системы векторов. Базис линейного пространства и координаты вектора в базисе.

Линейной комбинацией векторов с коэффициентами называется выражение вида: .

Вектора называются линейно независимыми, если , из которых хотя бы одно отлично от нуля, т.е. линейная комбинация с этими является нулевым вектором V, т.е. . Вектора , не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что

Теорема 1.

1) Для того, чтобы элементы были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов был линейной комбинацией остальных.

2) Если среди один элемент нулевой, то они линейно зависимы.

3) Если часть элементов множества линейно зависима, то и все элементы линейно зависимы.

Базис линейного пространства и координаты вектора в базисе.

Совокупность векторов называют базисом в , если

1^о. вектора – линейно независимы;

2^о. для найдутся . (1)

При этом равенство (1) называется разложением элемента по базису , а называются координатами относительно базиса .

Теорема: (о единственности разложения по базису). Любой элемент может быть единственным образом разложен по базису , т.е. координаты вектора относительно базиса определяются однозначно.

Доказательство. Пусть и . Тогда . В силу линейной независимости . ч.т.д.

Теорема : (операции над векторами, заданными своими координатами). При сложении любых двух векторов и их координаты (относительно любого фиксированного базиса в ) складываются; при умножении на , все координаты вектора умножаются на это число.

Доказательство. Пусть - базис в , , . Тогда в силу аксиом линейного пространства , . В силу единственности разложения по базису что теорема доказана.

Примеры. 1^о. Базис в - любое ненулевое число.

2^о. . Базис образуют матрицы , , …, с одним единичным элементом.

3^о. – множество многочленов степени не выше n. Базис: , , …, .

Базис векторного пространства и его размерности.

Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.

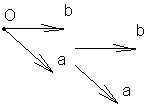
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

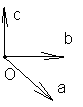
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе

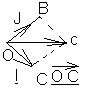
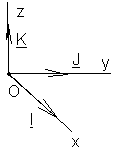
Вектора

Теорема

Система векторов A1,…..,Ak линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

Доказательство. Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов j1,j2,..jk , что j1*A1 + j2*A”+…jk*Ak=0 , причем хотя бы один коэффициент отличен от нуля. Предположим, что A1 !=0 . Тогда

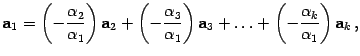
то есть A1 является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор A1 , то есть A1 = v2*A2+v3*A3+…+vk*Ak . Очевидно, что –A1+v2A2+…+vkAk=0 . Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен -1 ).

Следующее предложение показывает геометрический смысл смешанного произведения.

Смешанное произведение abc некомпланарных векторов равно объему параллелепипеда, сторонами которого служат векторы a,b,c, взятому со знаком " + ", если векторы образуют правую тройку, и со знаком " - ", если -- левую.

Доказательство. Пусть d = b x c . По предложению 10.22 |d| равен площади S параллелограмма, сторонами которого служат векторы b,c (рис. 10.26, 10.27).

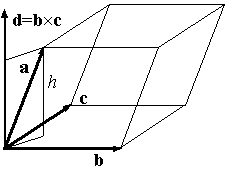
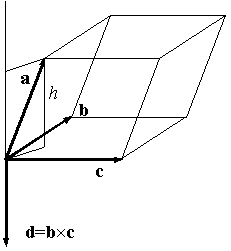
По свойству 7 скалярного произведения ( теорема 10.2)

Пусть h -- высота параллелепипеда (рис. 10.26, 10.27). Если a,b,c -- правая тройка векторов, то Пр a(на d) =h (рис. 10.26),

Если a,b,c -- левая тройка, то Пр а(на d) = -h . Так как S*h=V -- объем параллелепипеда, то из формулы (10.7) получим

Abc=V в случае правой тройки и abc= -V в случае левой тройки сомножителей.

Заметим, что если тройка векторов a,b,c является правой, то тройки c,a,b и b,c,a также будут правыми, а тройки b,a,c, c,b,a и a,c,b будут левыми тройками векторов.

Так как объем параллелепипеда не зависит от того, в каком порядке перечисляются его стороны, то abc=cab=bca=-bac=-cba=-acb

Представление векторного произведения через координаты векторов.

Пусть a = (A1,A2,A3), b = (B1,B2,B3) . Тогда

Доказательство. По условию a = A1*i+A2*j+A3*k , b = B1*i+B2*j+B3*k . В силу предложений 10.20 и 10.21 получим

По тем же правилам

По таблице умножения i x b = B2*k – B3*j . Аналогично находим j x b = -B1*k + B3*i , k x b = B1*j – B2*i . Подставив полученные результаты в формулу (10.5), получим

Представление скалярного произведения через координаты векторов.

Если векторы в ортонормированном базисе заданы своими координатами a = (A1,A2,A3) , b = (B1,B2,B3) , то

Доказательство. По условию a = A1*i+A2*j+A3*k , b = B1*i+B2*j+B3*k . В силу свойств 1 - 3 ( теорема 10.2) скалярного произведения получим

Используя те же свойства, находим a*i = (A1*i+A2*j+A3*k)*i = A1*i^2+A2*j*i+A3*k*i . В силу свойства 5, находим i^2=1 , а по свойству 8 получим j*i=k*i =0 . Таким образом, a*i=A1 . Аналогично находим, что a*j=A2 , a*k=A3 . Подставив полученные результаты в формулу

Получим исходную формулу.

Если в правом ортонормированном базисе i,j,k заданы координаты векторов a = (A1,A2,A3) , b = (B1,B2,B3) , то

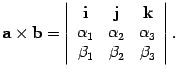
Доказательство. Достаточно лишь написать формулу вычисления приведенного в теореме определителя и сравнить ее с формулой

Смешанное произведение.

Пусть в правом ортонормированном базисе i,j,k заданы векторы a = (A1,A2,A3) , b = (B1,B2,B3) , c = (Y1,Y2,Y3) . Тогда

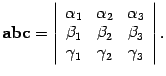
Доказательство. По предложению 10.25 находим координаты вектора b x c :

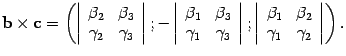
По теореме 10.3 находим скалярное произведение вектора a на вектор b x c :

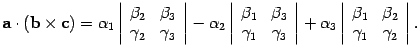
Правая часть этого неравенсва совпадает с определением определителя

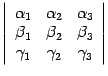
По определению a*b*c = a*(b x c)

Что и требовалось доказать.

Свойство дистрибутивности скалярного произведения.

a(b+c)=ab+ac;

Докажем/ В силу свойства 7:

Если a !=0

имеем a(b+c) = |a|*Пр(b+c) на a. Т.к. Пр(b+c) на a=Пр b на a + Пр c на a. Поэтому

Если же а =0 то св-во очевидно.

Распределительное свойство векторного произведения.

Векторное произведение обладает свойством дистрибутивности, то есть a x (b+c)= a x b + a x c.

Доказательство. Выберем в пространстве правый ортонормированный базис i,j,k. Пусть d = a x (b+c)

d = (A,B,Y), d1=a x b, d1=(A1,B1,Y1), d2 = a x c, d2 = (A2,B2,Y2). Нам нужно доказать, что d = d1 + d2 , то есть что

выполняются равенства: A = A1 + A2, B = B1 + B2.

Т.к. Проекции вектора на координатные оси равны коодинатам вектора, то

По свойству линейности смешанного произведения

Аналогично доказываются равенства B = B1 + B2, Y = Y1 + Y2.