28. Спектральний аналіз періодичних сигналів

Періодичним називається будь-який сигнал, для якого виконується умова: T- період.

Будь-який періодичний сигнал можна представити у виді суми елементарних складових (базисних функцій). Якщо базисною функцією є гармонійний сигнал то ряд Фур'є має вид:

Спектр ф-ції – графічне представлення ряду Фур’є.

Прямокутні сигнали мають спектр у вигляді арочного синуса. При цьому виникає залежність: q=T/ti

АЧС і ФЧС

Амплітудно-частотна і фазочастотна характеристики цілком визначають структуру спектра періодичного коливання.

Особливий інтерес представляє АЧС, що дозволяє судити про відсотковий склад тих або інших гармонік у спектрі періодичного сигналу. Спектр періодичного сигналу, називають лінійчатим або дискретним спектром, тому що він складається з окремих ліній , пропорційних ампліту амплітуді косинусів розташованих на окремих частотах, що йдуть із кроком .

29. Спектральний аналіз періодичних сигналів. Комплексна форма ряду Фур’є. Поняття негативної частоти.

Періодичним називається будь-який сигнал, для якого виконується умова: T- період.

Будь-який періодичний сигнал можна представити у виді суми елементарних складових (базисних функцій). Якщо базисною функцією є гармонійний сигнал то ряд Фур'є має вид:

Спектр ф-ції – графічне представлення ряду Фур’є.

Прямокутні сигнали мають спектр у вигляді арочного синуса. При цьому виникає залежність: q=T/ti

АЧС і ФЧС

Амплітудно-частотна і фазочастотна характеристики цілком визначають структуру спектра періодичного коливання.

Особливий інтерес представляє АЧС, що дозволяє судити про відсотковий склад тих або інших гармонік у спектрі періодичного сигналу. Спектр періодичного сигналу, називають лінійчатим або дискретним спектром, тому що він складається з окремих ліній , пропорційних ампліту амплітуді косинусів розташованих на окремих частотах, що йдуть із кроком .

Так, як базова складова ряду Фур’є – це найпростіший гармонічний сигнал, то на основі перетворень Ейлера розкладемо його:

A*cos(nw1t)= A/2*e + A/2*e ;

Введення від’ємної частини – це лище припущення для спрощення обрахунків. Вектор обертається проти годинникової стрілки з позитивною частотою з позитивною частотою. Вектор обертається за годинниковою стрілкою з негативною частотою. Негативна частота носить чисто математичний характер відповідний комплексному розкладання і жодного фізичного сенсу не має.

Тригонометричний ряд: Ċn=(an-j*bn)/2; Čn=(an+j*bn)/2;

= > S(t)=C0+∑Ċn*e +∑Čn*e ;

В непарній функції по синусу Ċn= Čn.

Отже, припущення про існування уявної області та негативної частоти для таких сигналів підтвердилося.

Ċn= 1/T ∫S(t)* e dt;

Ċn=An/2=(√an?+ bn?)/2

30,31 Модульовані сигнали. Амплітудна модуляція. Модульовані сигнали. Амплітудна модуляція. Спектр однотональних ам коливань.

Одна из задач РТ это передача информации. Для передачи информационных сигналов используются высоко частотные электромагнитные колебания, которые возможно эффективно использовать при малых мощностях передатчика. Важным условием для выбора ВЧ передачи является способность данной длины волны распространяться в пространстве. Передаваемая информация (информационный сигнал) должен тем или иным способом быть заложен в ВЧ колебание, которое в данном случае будет являться носителем информации. Данный процесс закладки информации в ВЧ сигнал осуществляется с помощью модуляции. Модуляцией называют процесс изменения параметров несущего колебания по закону информационного сигнала В самом общем случае модулирующий сигнал можно представить в виде (1)

В формуле (1) и изменяются по закону информационного сигнала. Если , то выражение (1) превращается в простой ВЧ гармонический сигнал. В этом случае он ни какой информации не несет. В зависимости от того какой из параметров ВЧ колебания изменяется, или различают два вида модуляций - амплитудную модуляци и угловую модуляцию. Угловая в свою очередь на основе природы изменения угла косинуса несущего колебания делится на фазовую и частотную. Закон изменения параметров и настолько медленно меняются, что их можно назвать низкочастотными или медленноменяющимися.

1.Амплитудная модуляция Однотональная.

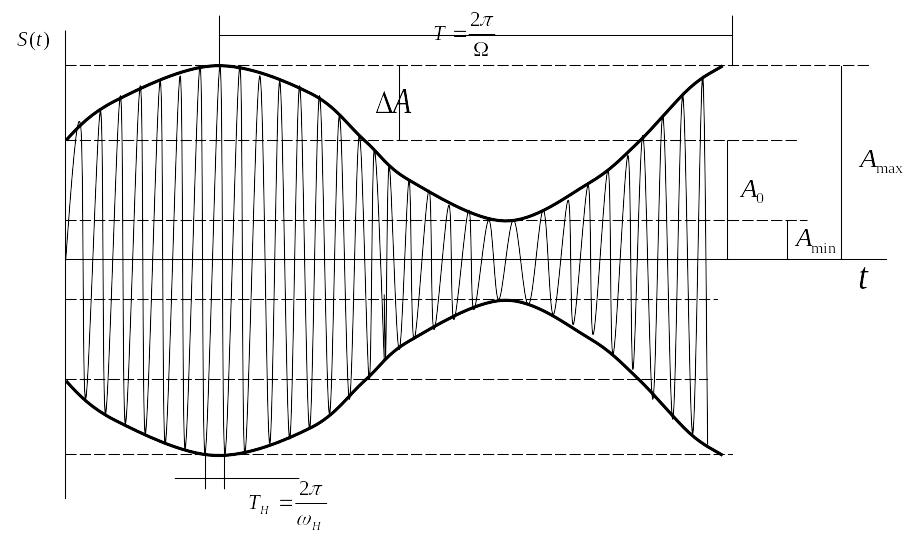
При АМ амплитуда несущего колебания является функцией времени и имеет вид.

где -постоянная составляющая ( среднее значение амплитуды модулируемого колебания), -функция времени, которая называется модулирующей функцией.Для одно-тональной модуляции формула АМ колебания записывается.

Если , тогда формула для однотональной АМ, при гармоническом законе изменения информационного сигнала примет вид. где - коэффициент модуляции, - частота модулирующего колебания, - начальная фаза модулирующего колебания

Коэффициент модуляции изменяется в пределах от нуля до единицы. Или в относительных единицах от нуля до 100%. где -глубина модуляции.Если -наблюдаем перемодуляцию.

В режиме перемодуляции происходит искажение сигнала информации

Спектр однотональных АМ колебаний.

На основе тригонометрических преобразований разложим АМ колебание на сумму элементарных функций.

- частота нижней боковой составляющей.

- частота верхней боковой составляющей.

- фаза нижней боковой составляющей.

- фаза верхней боковой составляющей.

АЧС однотональных АМ-колебаний. ФЧС.

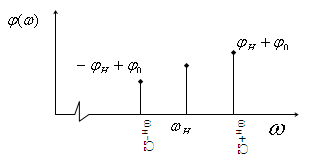
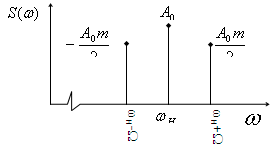
-полная фаза это угол косинуса несущего колебания.Для АМ-колебания полная фаза равна:

Вводится понятие мгновенной частоты - скорости изменения полной фазы (первая производная от полной фазы).