9,13. Властивість дійсної та уявної частини спектральної щільності. Лінійність перетворення Фур'є
Между сигналом и его спектральной плотностью существует однозначное соответствие. Для практических приложений важную роль играет связь между преобразованием сигнала и соответствующему этому преобразованию изменение спектра
Рассмотрим основные свойства преобразований Фурье.
1.Линейность
преобразования Фурье
Если имеется некоторая совокупность
сигналов
,
,…и
т.д., причем
,
,…и
т. д., то взвешенная сумма сигналов
преобразуется в следующем виде.
(8)
-произвольные
числовые коэффициенты.
2.Свойство вещественной и мнимой части спектральной плотности.
Пусть -сигнал, принимающий вещественные значения. Его спектральная плотность в общем случае является комплексной величиной, а следовательно может быть представлена в виде.
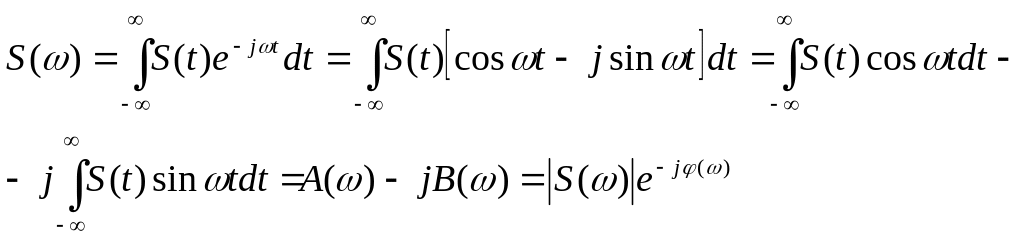
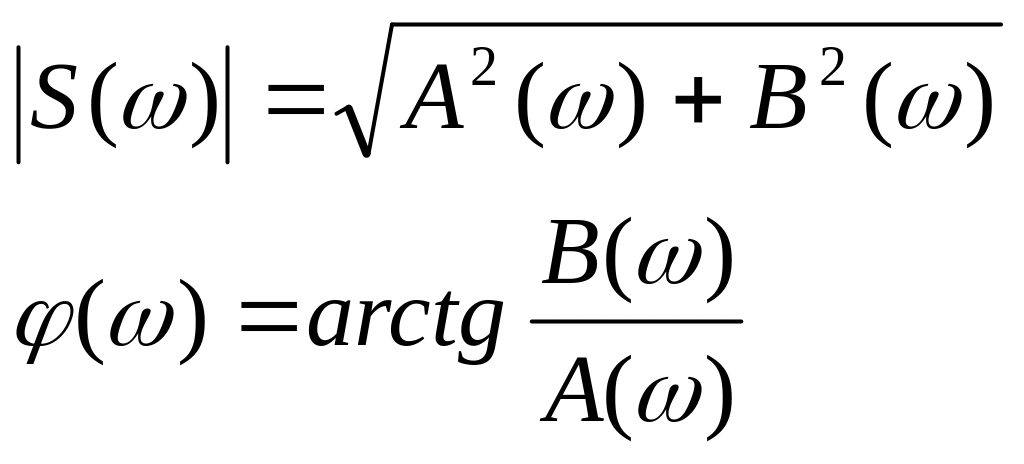
Величины
и
представляют собой соответственно
вещественную и мнимую части спектральной
плотности.
и
-модуль
и аргумент спектральной плотности.
(9 Подставим (2) в ОПФ.
Из
(3) видно, что сигнал будет вещественным
только в том случае, когда
Это возможно лишь в том случае, если вещественная часть -четная функция, а мнимая часть -нечетная функция.
(10)
При этом подынтегральные выражения в симметричных пределах равны нулю.
10. Залежність спектральної щільності сигналу від вибору масштабу виміру часу.
Пусть
сигнал
с
заданной внутренней структурой
подвергается во временной области
сжатию в
-раз.
При этом форма и амплитуда сигнала
сохранены.
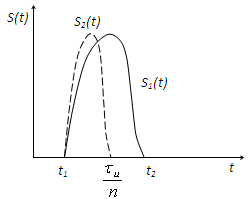
Новый
сигнал
связан с исходным соотношением
,
где
.
Длительность сигнала
в
-раз
меньше сигнала
.
Спектральная плотность сжатого сигнала
равна:
(12*)
Интеграл
в правой части (5) представляет собой
спектральную плотность исходного
сигнала
при частоте
,
т.е.
.
Таким образом соотношение (12*) устанавливает соответствие между изменением масштаба времени в -раз и эквивалентным ему преобразованием спектральной плотности. Из данного выражения (12) видно, что сжатие сигнала по оси времени в -раз, во столько же раз расширяет его спектр. Амплитуда при этом уменьшается в -раз. Выполняется обратная зависимость : чем протяженней по времени сигнал, тем уже его спектр. Чем короче по времени сигнал, те шире его спектр.
11. Зв'язок між тривалістю імпульсу і шириною його спектра.
Если проанализировать частные случаи, то можно сделать вывод: чем меньше длительность импульса, тем шире его спектр.
Под
шириной спектра обычно понимают частотный
интервал в пределах которого спектральная
плотность на меньше какого-то наперед
заданного значения. Например изменяется
в пределах
Спектр дельта импульса (длительность бесконечно мала) значит ширина спектра бесконечно велика.
Вывод: произведение ширины спектра импульса на его длительность есть постоянное число, зависящее только от формы импульса.
12. Комплексна форма ряду Фур’є. Поняття негативної частоти.
Так, як базова складова ряду Фур’є – це найпростіший гармонічний сигнал, то на основі перетворень Ейлера розкладемо його:
A*cos(nw1t)= A/2*e + A/2*e ;
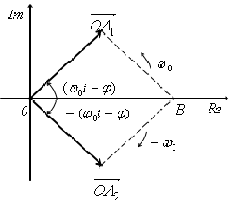
Введення від’ємної частини – це лище припущення для спрощення обрахунків. Вектор обертається проти годинникової стрілки з позитивною частотою з позитивною частотою. Вектор обертається за годинниковою стрілкою з негативною частотою. Негативна частота носить чисто математичний характер відповідний комплексному розкладання і жодного фізичного сенсу не має.
Тригонометричний ряд: Ċn=(an-j*bn)/2; Čn=(an+j*bn)/2;
= > S(t)=C0+∑Ċn*e +∑Čn*e ;
В непарній функції по синусу Ċn= Čn.
Отже, припущення про існування уявної області та негативної частоти для таких сигналів підтвердилося.
Ċn= 1/T ∫S(t)* e dt;
Ċn=An/2=(√an?+ bn?)/2