2.1.2. Математический маятник

В качестве примера гармонических колебаний рассмотрим малые колебания математического маятника - материальной точки массой m, подвешенной на невесомой и нерастяжимой нити длинной l в поле тяжести Земли. Когда маятник висит вертикально, сумма сил действующих на частицу (силы тяжести, действующая со стороны Земли, mg, и силы натяжения нити )

= 0 (30)

т.е. частица массы m находится в равновесии.

Сместим частицу m из положения равновесия по дуге окружности радиуса l на величину

α = l θ , (31)

где θ – угол отклонения нити (в радианах) (рис.4а). При этом сила тяжести останется без изменений, в то время как сила натяжения нити изменяется не только по направлению, но и по величине, в итоге результирующая сила , действующая на частицу, станет отличной от нуля и будет направлена к положению равновесия (т.е. эта сила возвращающая, восстанавливающая, а положение равновесия устойчивое). Из рис. 4а видно, что

F_x = - mg sin θ (32)

или, используя (31),

F_x = - mg sin (x/l) (33)

Из (33) следует, что возвращающая сила F_x зависит от x по нелинейному закону. Следовательно, колебания математического маятника в общем случае не являются гармоническими. Однако, в случае малых колебаний, когда выполняется условие x << l, отношение x/l << 1 и и sin (x/l) tg (x/l) x/l. Поэтому при малых колебаниях возвращающая сила

F_x = - mg (34)

линейно зависит от x, причем коэффициент возвращающей силы

k = . (35)

Таким образом, при малых смещениях от положения равновесия математический маятник колеблется по гармоническому закону

x(t) = A cos(ω₀t + α)

с частотой

ω₀ = = (36)

и периодом

T = = 2π . (37)

Отметим, что длина маятника с периодом колебаний T₀ = 1 с (для стандартного значения ускорения свободного падения вблизи поверхности Земли g₀ = 9,81 м/с²) равна 24,8 см.

Если маятник находится в глубокой шахте на глубине h или на вершине горы высотой h (не на борту спутника), то его период колебаний будет определяться ускорением свободного падения в месте нахождения маятника. Если не учитывать вращение Земли и воспользоваться выражениями для g в шахте на глубине h, то получим, что на этой глубине

T = 2π 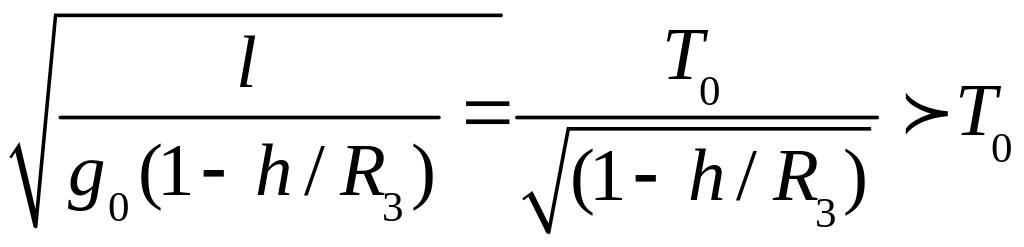(38)

(где T₀ – его период колебаний на поверхности Земли и R₃ – радиус Земли), а на высоте h

T = 2π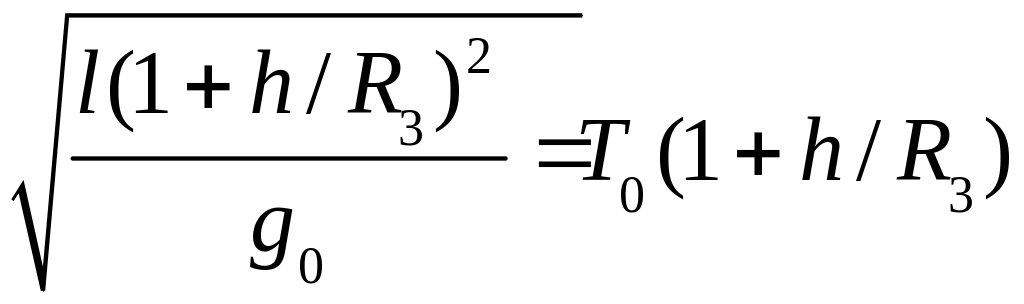 > Т₀ . (39)

Отметим, что в случае, когда глубина шахты h << R₃, стоящий в (38) сомножитель 1/ можно приближенно заменить на (1 + h/2R₃). В этом случае период колебаний маятника

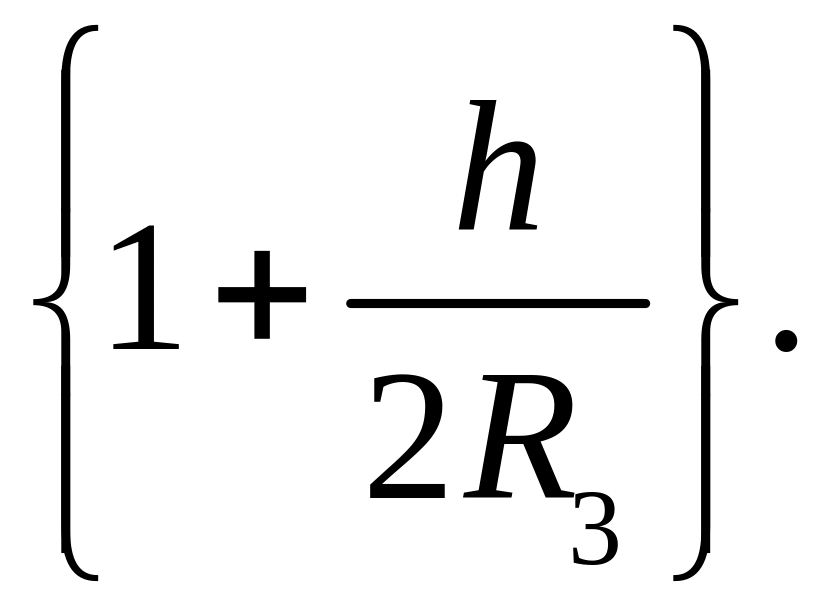T T₀ (40)

Рассмотрим теперь вопрос о том, как изменяется колебательное движение математического маятника, если на материальную точку, кроме силы тяжести, действует еще постоянная внешняя си

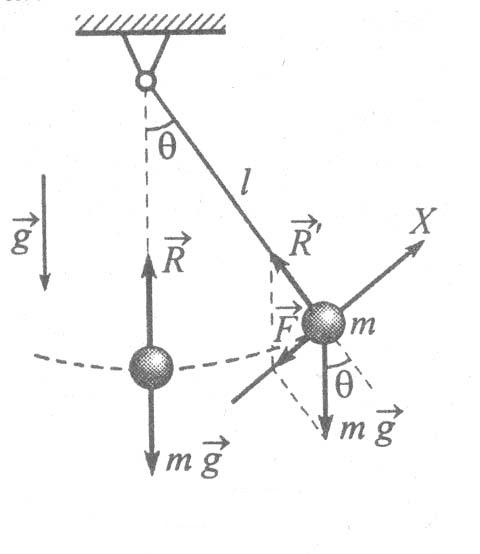
Рис.4а. Математический маятник и действующие на него силы

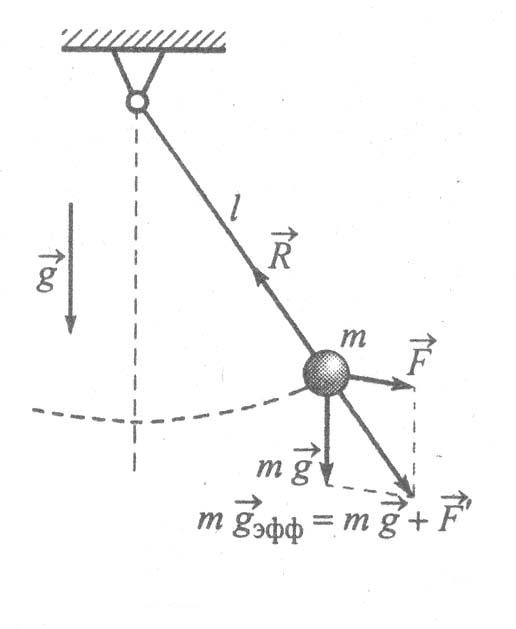
Рис.4б. Математический маятник под действием сторонней силы

ла (например, сила Архимеда, когда маятник движется в жид- кости).

В положении равновесия равнодействующая всех сил, действующих на частицу

= 0 (41)

Из (41), в частности, следует, что в положении равновесия векторы (вертикаль), (нить) и лежат в одной плоскости.

Соотношение (41) можно записать в виде

(42)

где

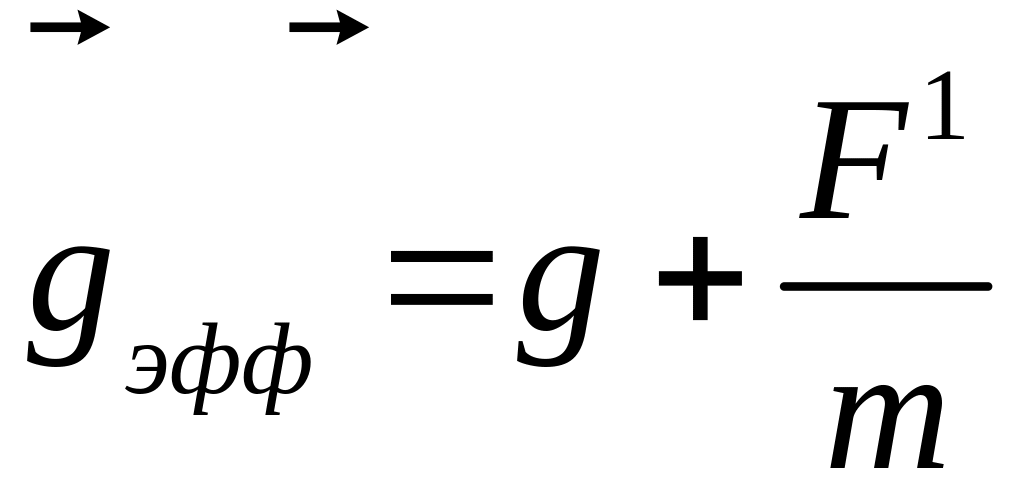(43)

т.е. в этом случае нить маятника в положении равновесия не вертикальна, а расположена вдоль вектора . Обратим внимание, что условие равновесия (42) формально совпадает с (30) с той лишь разницей, что в (30) стоит , а в (42) - . Поэтому, все формулы, написанные после (30) и относящиеся к выражению периода колебания математического маятника, остаются в силе и в нашем случае, если в них заменить , на . Таким образом, при действии на маятник постоянной силы он будет совершать малые гармонические колебания около положения равновесия, в котором нить расположена вдоль вектора , с частотой

ω₀ = 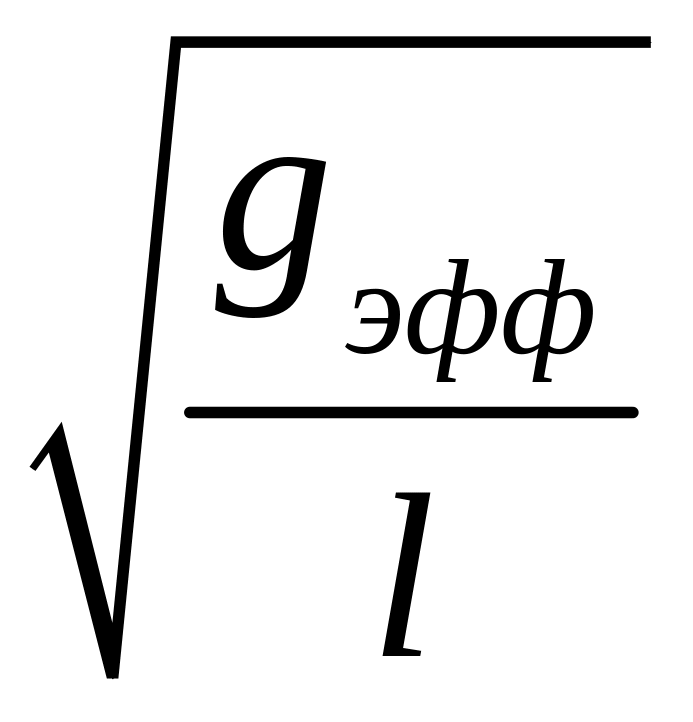(44)

и периодом

T = 2π 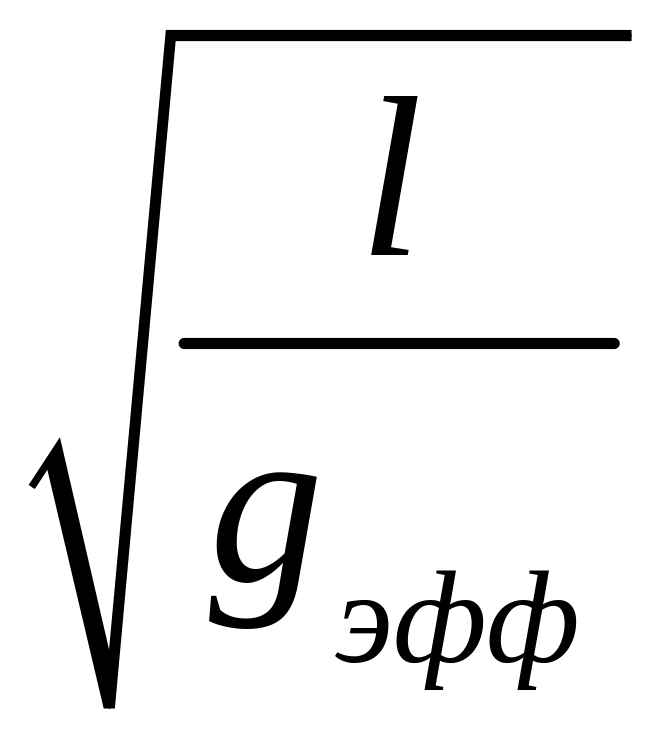, (45)

где

g_эфф = 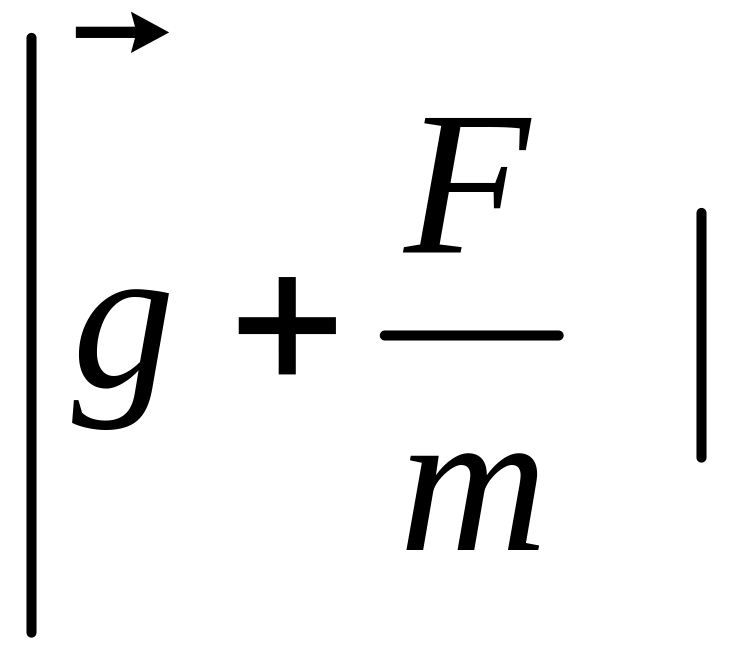(46)

- абсолютное значение (модуль) вектора .

Полученные выше результаты можно использовать при рассмотрении задачи о гармонических колебаниях математического маятника, когда его точка подвеса движется относительно Земли с постоянным ускорением . Для этого перейдем в неинерциальную систему отсчета, связанную с точкой подвеса. Как известно, закон движения материальной точки (второй закон Ньютона) в неинерциальной системе отсчета совпадает с законом движения ее в инерциальной системе отсчета, если считать, что на эту точку, кроме реальных сил, действует также фиктивная сила инерции . На основании этого можно заключить, что в случае, когда точка подвеса математического маятника движется с постоянным ускорением , маятник может совершать малые гармонические колебания около положения устойчивого равновесия, в котором нить маятника расположена вдоль вектора

= (47)

с частотой (44) и периодом (45), где

g_эфф = .

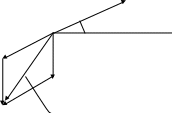
Задача 1. Самолет стартует под углом α к горизонту с ускорением а (рис.5). Найти частоту малых колебаний математического маятника длины l, подвешенного в самолете.

Решение

Найдем эквивалентное ускорение g^ обусловленное инерционными силами и силой тяжести (рис. 5). Из чертежа, используя теорему косинусов, имеем:

(g^')² = а² + g² + 2аg sin α . (48)

Далее используем соотношение ω² = g¹ /l.

Рис. 5. Векторы сил и ускорений (к задаче 1)