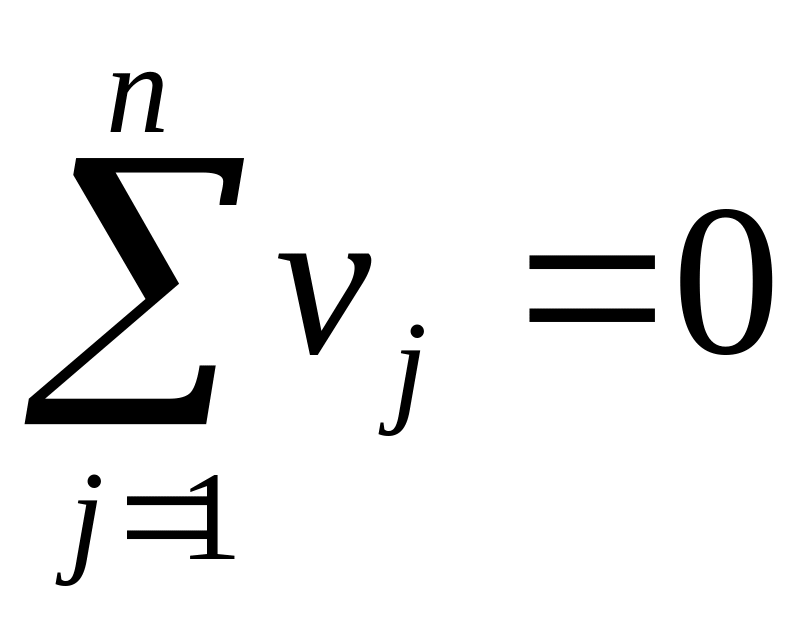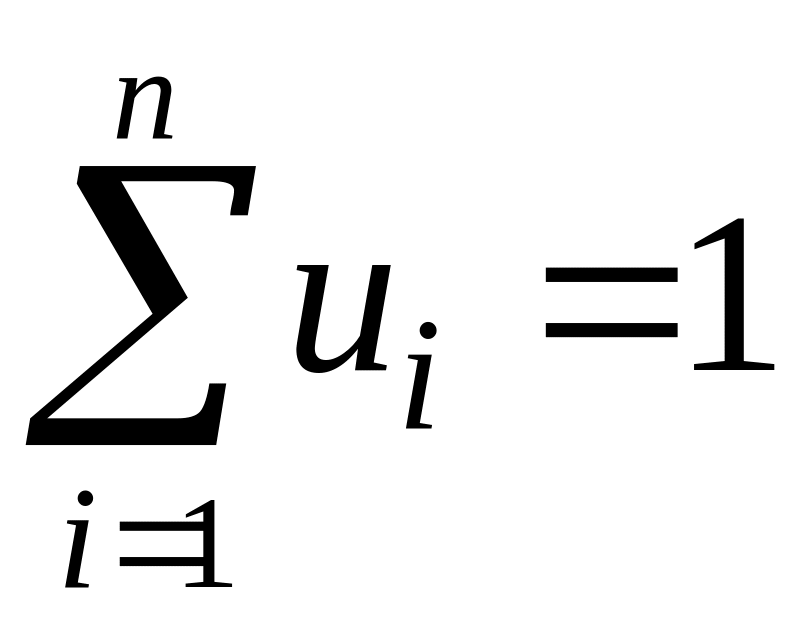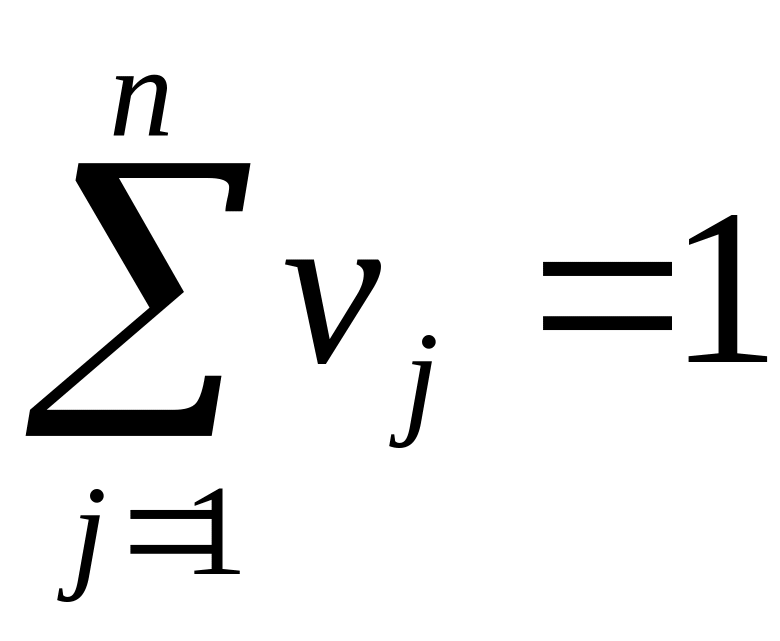- •Методическое руководство по выполнению курсовой работы
- •B ведение
- •Раздел 3 содержит материал, который будет полезен для правильного оформления курсовой работы.
- •1.2 Задание 1
- •Варианты задания 1
- •2 Pасписания
- •2.1 Минимизация длины расписания для системы поточного типа (Fm| |Cmax)
- •2.2 Задание 2
- •Варианты задания 2
- •2.3 Минимизация максимального времени обслуживания требований с различными маршрутами
- •2.4 Задание 3
- •Варианты задания 3
- •3 Методические указания по оформлению курсовой работы
- •Требования к оформлению курсовой работы
- •Условные обозначения и сокращения
- •Список литературы
- •Применение методов теории расписаний в управлении воздушным движением и обеспечении безопасности полетов
1.2 Задание 1
Описание задачи
Летчику надо облететь пять городов так, чтобы вылетев из одного города, облететь все города только один раз, вернуться в исходный город и при этом пролететь путь минимальной длины.
Расстояние между городами задается матрицей расстояний
A5*5
=
{ai,j},
i,
j =
![]() .
.
Типовой пример выполнения задания 1
Дано: n = 5;
значения элементов матрицы А (матрицы расстояний):
А
=
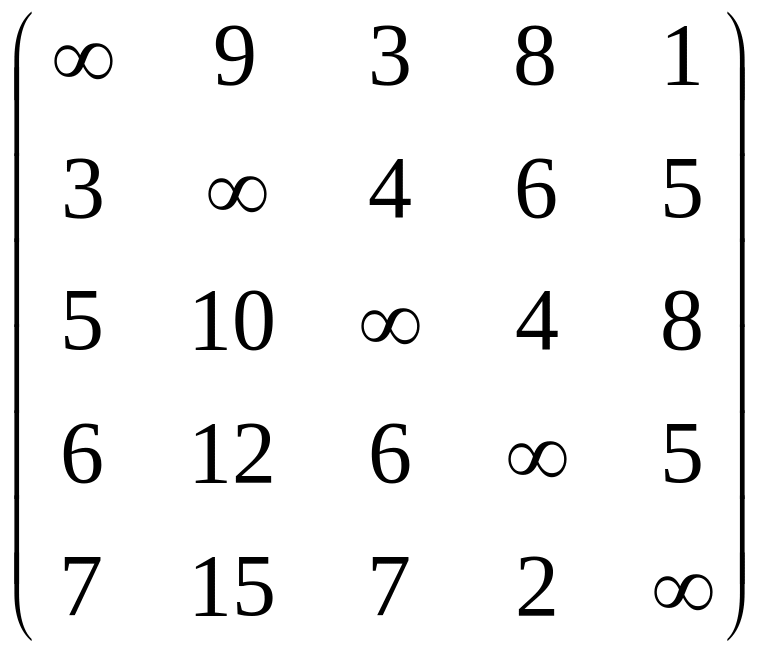 .
.
Матрица A5*5 = {ai,j}, i, j = , называется матрицей расстояний, в ней каждым элементом ai,j задается расстояние из города i в город j .
Решение
Если города представить в виде вершин графа, а связь между городами (i, j) в виде направленной дуги, то получится ориентированный граф (орграф), с помощью которого графически можно представить задачу задания 1 (рисунок 1.1).
7
9
5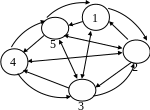
3
2
4
4
10
6
Рисунок 1.1 – Орграф задачи задания 1
В нашем случае связь между городами (i, j) это пути из города i в город j, длина которых задана матрицей расстояний А. Решение данной задачи заключается в нахождении в полученном орграфе гамильтонова контура минимальной длины.
Задача задания 1 в рамках теории расписаний представляет собой задачу минимизации суммы переналадок одного прибора. Она сводится к задаче «о бродячем торговце», которая решается методом «ветвей и границ». Этим методом и будем решать задачу. Для этого надо сделать следующее.
1
Представим матрицу А
в виде таблицы, справа присоединим
столбец для элементов
![]() ,
,
![]() ,
найдем их и просуммируем:
,
найдем их и просуммируем:
|
i |
j |
ui |
|
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
||
|
1 |
|
9 |
3 |
8 |
1 |
1 |
|
|
А = |
2 |
3 |
|
4 |
6 |
5 |
3 |
|
|
3 |
5 |
10 |
|
4 |
8 |
4 |
|
||
|
4 |
6 |
12 |
6 |
|
5 |
5 |
|
|
|
5 |
7 |
15 |
7 |
2 |
|
2 |
||
2 Вычтем элементы ui из соответствующих элементов матрицы А. Получим матрицу А, приведенную по строкам:
|
i |
j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
|
8 |
2 |
7 |
0 |
А = |
2 |
0 |
|
1 |
3 |
2 |
|
3 |
1 |
6 |
|
0 |
4 |
|
4 |
1 |
7 |
1 |
|
0 |
|
5 |
5 |
13 |
5 |
0 |
|
3
Присоединим снизу строку для
элементов
![]() ,
,
найдем их и просуммируем:
,
,
найдем их и просуммируем:
|
i |
j |
|
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
1 |
|
8 |
2 |
7 |
0 |
|
|
2 |
0 |
|
1 |
3 |
2 |
|
|
3 |
1 |
6 |
|
0 |
4 |
|
|
4 |
1 |
7 |
1 |
|
0 |
|
|
5 |
5 |
13 |
5 |
0 |
|
|
|
vj |
0 |
6 |
1 |
0 |
0 |
|
4 Вычтем элементы vj из соответствующих элементов
матрицы А и получим матрицу А, приведенную по строкам и столбцам:
|
i |
j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
|
2 |
1 |
7 |
0 |
А" = |
2 |
0 |
|
0 |
3 |
2 |
|
3 |
1 |
0 |
|
0 |
4 |
|
4 |
1 |
1 |
0 |
|
0 |
|
5 |
5 |
7 |
4 |
0 |
|
5 Найдем константу приведения:
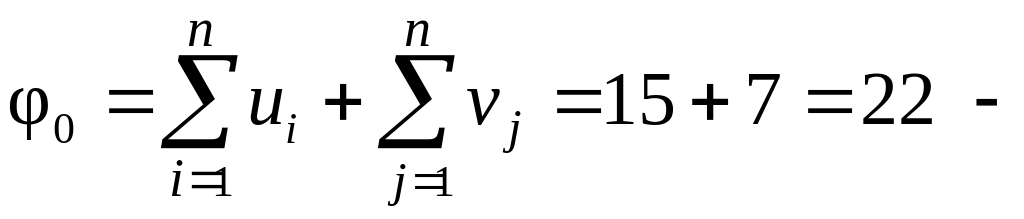
это нижняя граница длин всех гамильтоновых контуров.
6 Найдем степень нулей для матрицы А. Для этого находим сумму минимальных элементов строки и столбца, на пересечении которых находится нуль матрицы А, степень которого определяется без учета значения самого рассматриваемого в данный момент нуля:
|
i |
j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
|
2 |
1 |
7 |
0(1) |
А" = |
2 |
0(1) |
|
0(0) |
3 |
2 |
|
3 |
1 |
0(1) |
|
0(0) |
4 |
|
4 |
1 |
1 |
0(0) |
|
0(0) |
|
5 |
5 |
7 |
4 |
0(4) |
|
Нуль, стоящий на
месте пересечения 1-й строки и 5-го
столбца, имеет степень
![]() +
+
![]() = 1 + 0 = 1.
= 1 + 0 = 1.
Примечание
–
![]() ,
потому что значение нуля, стоящего на
месте пересечения 1-й строки и 5-го
столбца, не учитывается, так как это
нуль, степень которого определяется.
,
потому что значение нуля, стоящего на
месте пересечения 1-й строки и 5-го
столбца, не учитывается, так как это
нуль, степень которого определяется.
Аналогично определяются степени остальных нулей матрицы А.
Выберем дугу, для которой степень нулевого элемента наибольшая. В нашем случае эта степень равна 4 и ее имеет нуль, стоящий на месте пересечения 5-й строки и 4-го столбца. Следовательно, выбираем дугу (5, 4).
7
Разобьем множество гамильтоновых
контуров 0
на два подмножества:
![]() и
и
![]() .
Подмножеству
,
содержащему дугу (5, 4), соответствует
матрица
.
Подмножеству
,
содержащему дугу (5, 4), соответствует
матрица
![]() ;
подмножеству
,
не содержащему дугу (5, 4), соответствует
матрица
;
подмножеству
,
не содержащему дугу (5, 4), соответствует
матрица
![]() .
.
8
Матрицу
получаем из матрицы А
(пункт 4) путем вычеркивания 5-й строки
и 4-го столбца. Для того чтобы не допустить
образования негамильтонова контура,
заменим симметричный относительно
главной диагонали элемент
![]() на символ ,
т. е.
на символ ,
т. е.
![]() .
Делаем дополнительное приведение
матрицы
и получаем матрицу
.
Делаем дополнительное приведение
матрицы
и получаем матрицу
![]() ,
которой будет соответствовать множество
,
которой будет соответствовать множество
![]() :
:
![]()
|
i |
j |
ui |
|
|||||
|
1 |
2 |
3 |
5 |
|
||||
|
1 |
|
2 |
1 |
0 |
0 |
|
||
= |
2 |
0 |
|
0 |
2 |
0 |
|
||
|
3 |
1 |
0 |
|
4 |
0 |
|
||
|
4 |
1 |
1 |
0 |
|
0 |
|||
|
vj |
0 |
0 |
0 |
0 |
|
|
||
9
![]() =
=
0.
=
=
0.
Находим дополнительную
константу приведения для подмножества
контуров
:
![]() =
=![]()
![]() = 22 + 0 = 22 – это нижняя граница для
подмножества
.
= 22 + 0 = 22 – это нижняя граница для
подмножества
.
10
Матрицу
получаем из матрицы А
(пункт 4) путем замены элемента
![]() на символ ,
т. е.
на символ ,
т. е.
![]() .
Делаем дополнительное приведение
матрицы
:
.
Делаем дополнительное приведение
матрицы
:
|
i |
j |
ui |
|
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
||
|
1 |
|
2 |
1 |
7 |
0 |
0 |
|
|
= |
2 |
0 |
|
0 |
3 |
2 |
0 |
|
|
3 |
1 |
0 |
|
0 |
4 |
0 |
|
||
|
4 |
1 |
1 |
0 |
|
0 |
0 |
= 4 |
|
|
5 |
5 |
7 |
4 |
|
|
4 |
||
11
Приводим матрицу
по строкам (по 4-й строке), присоединим
снизу строку для элементов
![]() ,
найдем их и просуммируем.
,
найдем их и просуммируем.
Так как все
минимальные элементы по столбцам равны
нулю, то приводить матрицу
по столбцам не надо. В результате получаем
матрицу
![]() ,
которой будет соответствовать
множество
:
,
которой будет соответствовать
множество
:
|
i |
j |
|
||||||
|
1 |
2 |
3 |
4 |
5 |
|
|||
|
1 |
|
2 |
1 |
7 |
0 |
|
||
= |
2 |
0 |
|
0 |
3 |
2 |
|
||
3 |
1 |
0 |
|
0 |
4 |
|
|||
|
4 |
1 |
1 |
0 |
|
0 |
|
||
|
5 |
1 |
3 |
0 |
|
|
|
||
|
vj |
0 |
0 |
0 |
0 |
0 |
|
||
12
![]() =
=
4 + 0 = 4.
=
=
4 + 0 = 4.
Находим
дополнительную константу приведения
для подмножества контуров
:
![]() =
+
=
22 + 4 = 26 – это нижняя граница для
подмножества
.
=
+
=
22 + 4 = 26 – это нижняя граница для
подмножества
.
13
Сравниваем нижние границы для
подмножеств
![]() и
.
и
.
Так как
![]() = 22 <
= 26, то дальнейшему ветвлению подвергаем
подмножество
.
= 22 <
= 26, то дальнейшему ветвлению подвергаем
подмножество
.
14
Для этого найдем степень нулей
для матрицы
![]() :
:
-
i
j
1
2
3
5
1
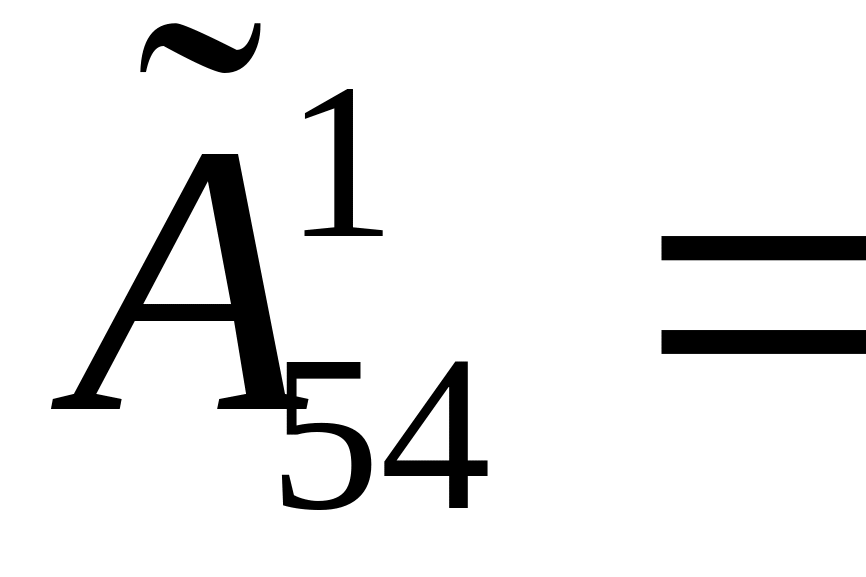
2
1
0(3)
2
0(1)
0(0)
2
3
1
0(2)
4
4
1
1
0(1)
15 Выберем дугу, для которой степень нулевого элемента наибольшая. В данном случае эта степень равна 3 и ее имеет нуль, стоящий на месте пересечения 1-й строки и 5-го столбца, т. е. выбираем дугу (1, 5).
16
Разобьем множество гамильтоновых
контуров
на два подмножества:
![]() и
и
![]() .
Подмножеству
,
содержащему дугу (1, 5), будет соответствовать
матрица
.
Подмножеству
,
содержащему дугу (1, 5), будет соответствовать
матрица
![]() ;
подмножеству
,
не содержащему дугу (1, 5), будет
соответствовать матрица
;
подмножеству
,
не содержащему дугу (1, 5), будет
соответствовать матрица
![]() .
.
17
Матрицу
получаем из матрицы
(пункты 8 и 14) путем вычеркивания 1-й
строки и 5-го столбца. Элемента
![]() в преобразуемой матрице нет.
в преобразуемой матрице нет.
Делаем дополнительное
приведение матрицы
и получаем матрицу
![]() ,
которой будет соответствовать множество
,
которой будет соответствовать множество
![]() :
:
|
i |
j |
ui |
|
|||||
|
1 |
2 |
3 |
|
|||||
|
2 |
0 |
|
0 |
0 |
|
|||
= |
3 |
1 |
0 |
|
0 |
|
|||
|
4 |
1 |
1 |
0 |
0 |
||||
|
vj |
0 |
0 |
0 |
|
|
|
||
18
![]() =
=
0.
=
=
0.
Находим дополнительную
константу приведения для подмножества
контуров
:
![]() =
+
=
22 + 0 = 22 – это нижняя граница для
подмножества
.
=
+
=
22 + 0 = 22 – это нижняя граница для
подмножества
.
19 Матрицу получаем из матрицы (пункты 8 и 14) путем замены элемента на символ , т. е. = . Делаем дополнительное приведение матрицы :
|
i |
j |
ui |
|
|||||
|
1 |
2 |
3 |
5 |
|
||||
|
1 |
|
2 |
1 |
|
1 |
|
||
= |
2 |
0 |
|
0 |
2 |
0 |
|
||
|
3 |
1 |
0 |
|
4 |
0 |
|
||
|
4 |
1 |
1 |
0 |
|
0 |
|||
20 Приводим
матрицу
по строкам (по 1-й строке). Присоединим
снизу строку для элементов
![]() ,
,
найдем их и просуммируем:
,
,
найдем их и просуммируем:
|
i |
j |
|
|||||
|
1 |
2 |
3 |
5 |
|
|||
|
1 |
|
2 |
1 |
|
|
||
|
2 |
0 |
|
0 |
2 |
|
||
|
3 |
1 |
0 |
|
4 |
|
||
|
4 |
1 |
1 |
0 |
|
|
||
|
vj |
0 |
0 |
0 |
2 |
|
||
Приводим полученную
матрицу по столбцам (по 5-му столбцу). В
результате получаем матрицу
,
которой будет соответствовать множество
![]() :
:
|
i |
j |
|||
|
1 |
2 |
3 |
5 |
|
|
1 |
|
1 |
0 |
|
|
2 |
0 |
|
0 |
0 |
|
3 |
1 |
0 |
|
2 |
|
4 |
1 |
1 |
0 |
|
21
![]() =
=
1 + 2 = 3.
=
=
1 + 2 = 3.
Находим дополнительную
константу приведения для подмножества
контуров
:
![]() =
=![]() = 22 + 3 = 25 – это нижняя граница для
подмножества
.
= 22 + 3 = 25 – это нижняя граница для
подмножества
.
22
Сравниваем нижние границы для подмножеств
и
.
Так как
![]() = 22 <
= 25, то дальнейшему ветвлению подвергаем
подмножество
.
= 22 <
= 25, то дальнейшему ветвлению подвергаем
подмножество
.
23 Для этого найдем степень нулей для матрицы :
|
i |
j |
||
|
1 |
2 |
3 |
|
|
2 |
0(1) |
|
0(0) |
= |
3 |
1 |
0(2) |
|
|
4 |
1 |
1 |
0(1) |
24 Выберем дугу, для которой степень нулевого элемента наибольшая. Эта степень равна 2, и ее имеет нуль, стоящий на месте пересечения 3-й строки и 2-го столбца. Значит, выбираем дугу (3,2).
25
Разобьем множество гамильтоновых
контуров
на два подмножества:
![]() и
и
![]() .
Подмножеству
,
содержащему дугу (3, 2), будет соответствовать
матрица
.
Подмножеству
,
содержащему дугу (3, 2), будет соответствовать
матрица
![]() ,
подмножеству
,
не содержащему дугу (3, 2), будет
соответствовать матрица
,
подмножеству
,
не содержащему дугу (3, 2), будет
соответствовать матрица
![]() .
.
26 Матрицу получаем из матрицы (пункты 17 и 23) путем вычеркивания 3-й строки и 2-го столбца. Для того чтобы не допустить образования негамильтонова контура, заменим симметричный относительно главной диагонали элемент на
символ ,
т. е.
![]() =
.
Делаем дополнительное приведение
матрицы
и получаем матрицу
=
.
Делаем дополнительное приведение
матрицы
и получаем матрицу
![]() ,
которой будет соответствовать множество
,
которой будет соответствовать множество
![]() :
:
|
i |
j |
ui |
|
||
|
1 |
3 |
|
|||
|
2 |
0 |
|
0 |
|
|
4 |
1 |
0 |
0 |
|||
|
|
0 |
0 |
|
|
|
27
![]() =
=
0.
=
=
0.
Находим дополнительную
константу приведения для подмножества
контуров
:
![]() =
=
![]() =
22 + 0 = 22 – это нижняя граница для
подмножества
.
=
22 + 0 = 22 – это нижняя граница для
подмножества
.
28
Матрицу
получаем из матрицы
(пункты 17 и 23) путем замены элемента
![]() на символ ,
т. е.
на символ ,
т. е.
![]() .
Делаем дополнительное приведение
матрицы
:
.
Делаем дополнительное приведение
матрицы
:
|
i |
j |
ui |
|
|||
|
1 |
2 |
3 |
|
|||
|
2 |
0 |
|
0 |
0 |
|
|
= |
3 |
1 |
|
|
1 |
|
|
|
4 |
1 |
1 |
0 |
0 |
||
29 Приводим
матрицу
по строкам (по 2-й строке), присоединим
снизу строку для элементов
![]() ,
найдем их и просуммируем:
,
найдем их и просуммируем:
|
i |
j |
|
|||||
|
1 |
2 |
3 |
|
||||
|
2 |
0 |
|
0 |
|
|||
|
3 |
0 |
|
|
|
|||
|
4 |
1 |
1 |
0 |
|
|||
|
vj |
0 |
1 |
0 |
|
|
||
Приведем
преобразуемую матрицу по столбцам (по
2-му столбцу) и получим матрицу
![]() ,
которой будет соответствовать множество
,
которой будет соответствовать множество
![]() :
:
|
i |
j |
||
|
1 |
2 |
3 |
|
|
2 |
0 |
|
0 |
= |
3 |
0 |
|
|
|
4 |
1 |
0 |
0 |
30
![]() =
=
1 + 1 = 2.
=
=
1 + 1 = 2.
Находим дополнительную
константу приведения для подмножества
контуров
![]() :
:
![]() =
=
![]() = 22 + 2 = 24 –
= 22 + 2 = 24 –
это нижняя граница для подмножества .
31
Сравниваем нижние границы для подмножеств
и
.
Так как
![]() = 22 <
= 24, то дальнейшему ветвлению подвергаем
подмножество
.
А так как матрица
имеет размерность 2 ×
2, то в гамильтонов контур следует
включить дуги, соответствующие в данной
матрице нулевым элементам, т. е. дуги
= 22 <
= 24, то дальнейшему ветвлению подвергаем
подмножество
.
А так как матрица
имеет размерность 2 ×
2, то в гамильтонов контур следует
включить дуги, соответствующие в данной
матрице нулевым элементам, т. е. дуги
(2, 1) и (4, 3). Таким образом, получен искомый гамильтонов
контур Г, который состоит из следующих дуг {(5, 4), (1, 5), (3, 2), (2, 1), (4, 3)} : Г = (5 4 3 2 1 5). Так как контур – это замкнутый путь, то его можно записать и так: Г = (1 5 4 3 2 1). Его длина Z (Г) = а15 + а54 + а43 + а32 + а21 = 1 + 2 + 6 + 10 + 3 = 22.
Процесс отыскания оптимального плана сопровождается построением дерева решений, которое представлено на рисунке 1.2.
Т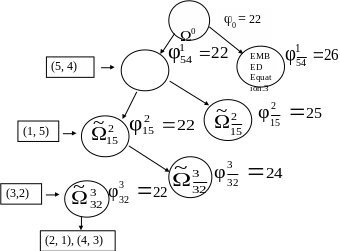 ак
как нижние границы оборванных ветвей
не меньше длины первого рекорда (см.
рисунок 1.2), то этот контур имеет наименьшую
длину. Значит, найденный гамильтонов
контур Г является оптимальным.
ак
как нижние границы оборванных ветвей
не меньше длины первого рекорда (см.
рисунок 1.2), то этот контур имеет наименьшую
длину. Значит, найденный гамильтонов
контур Г является оптимальным.
Рисунок 1.2 – Дерево поиска решений
На рисунке 1.3 представлен замкнутый контур минимальной длины, соответствующий оптимальному гамильтонову контуру Г.
3







 2
2




10

6
Рис. 1.3 – Оптимальный гамильтонов контур
Вывод: летчик должен сначала прилететь в город 1, затем в 5, 4, 3, 2 и вернуться в город 1, проделав при этом путь минимальной длиной в 22 единицы.

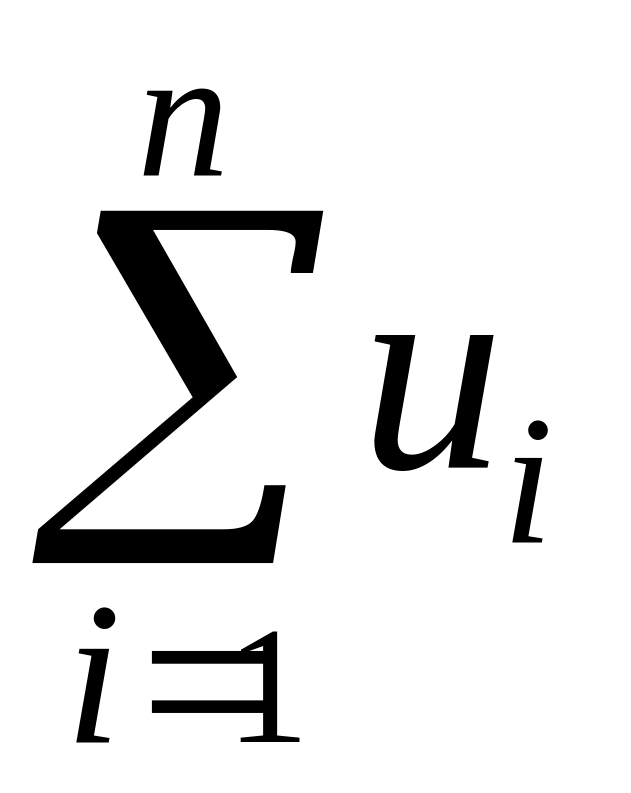 =
15
=
15