8. Критерій Коші збіжності числової послідовності.

Критерій Коші. Для того, щоб послідовність мала скінчену границю, необхідно і достатньо, щоб вона була фундаментальна.

Lim Xn=a, aєR => {Xn}фундаментальна.

n→∞

Дов.(для цього попередньо доведемо три леми) попереднє питання!!!

Леми доведено,тепер на основі цього доведемо Критерій Коші.

Дов. Необхідність випливає із ЛЕМИ 1

Достатність: {Xn}-ф. => за ЛЕМОЮ 2{Xn} обмежена => за теоремою Больцана-Вейерштрасса(№2) {Xn_k}→a, aєR => за ЛЕМОЮ 3 lim Xn=a

k→∞ n→∞

Що вимагалося довести.

Заув. Критерій Коші дає необх і достат умову збіж послідовностей ,в термінах тільки самих членів послідовності без використ значення границі.

Лема1 Якщо послідовність збіжна, то вона ф.Доведення: Нехай

, - фундаментальна за означенням

Лема2.Якщо послід ф,то вона обмеж.

_{Доведення}:В умові Коші покладемо Виберемо , тоді _.

Оберемо . Отже,

,

Лема3:Якщо деяка підпослід ф послід збіжна,то її границя є гран усієї ЧП.

Доведення: Нехай - фундаментальна.

За умовою Коші

Оберемо так, щоб виконувалось

_{Перейдемо до границі, коли}

9. Число як границя збіжної монотонної послідовності.

Застосуємо теорему про існув границі монот послід (ця теорема звучить: якщо неспадна (незростаюча) послід {x_n} обмежена зверху(знизу),то вона збіжна) для доведення існування границі послід {x_n}, елемент якої x_n знаходиться за формулою:

x_n =(1+1/n)ⁿ.

Доведемо, що ця послід зростає і обмеж зверху. Застосувавши ф-лу бінома Ньютона, знайдемо .

Представимо цей вираз в наступній формі:

(1)Аналогічно запишемо елемент x_n+1 :

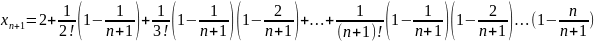
Порівнявши дані ф-ли, можна зробити висновок, що x_n<x_n+1,тобто послід {x_n} зростаюча.

Для довед обмеж цієї послід зверху помітимо, що кожен вираз в круглих дужках в співвідношенні (1) меньше 1. Враховуючи також, що при k>=2 отримаємо .

Отже, послід {x_n} зростає і обмежена зверху, тобто вона має границю.

Цю границю назив числом е. Тобто,

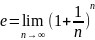
10. Озн.Коші:

Озн1: Функція f(x) має границею число коли , якщо для такий, що .

Позн1: ;

.

Теор: Озн-ня за Гейне і Коші границі функції в точці дотикання множини визначення фун-ії рівносильні.

Довед: (за Гейне) (за Коші).

Від супротивного:

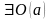
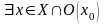
1)Нехай Утворимо послідовність околів т.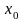 , тоді відповідно до припущення ;

Зауважимо, що за означенням гейне в силу означ границі послід – суперечність

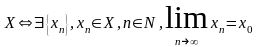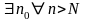
2) Нехай - точка дотикання ; за озн Коші ; .отже, вик умови озн гейне.

Озн: Ф-я f(x) наз. неперервною в т. , якщо

Заув! f(x)-неперервна в т. тоді і тільки тоді, коли 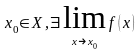. Дійсно, якщо взяти послідовність виконується .

11. Озн. За Гейне границі ф-ї. Точка дотикання множини

Нехай розгляд ф-я

Озн1(За Гейне): Точка наз. границею ф-ії f(x) при , якщо для будь-якої послідовності точок множини Х такої, що .

Озн1' такої, що : . .

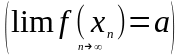Заув!Озн1 має зміст лише тоді, коли точок з Х, що .

Якщо аєR, то кажуть, що ф-я має скінченну границю.

Точка дотикання: Озн2: Точка наз. точкою дотикання множини Х, якщо існує послідовність точок та .

Заув! Якщо 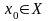, то є точкою дотикання Х. Точка дотикання може належати чи не належати множині. Якщо Х необмежена зверху(знизу), то точкою дотикання є .

Теор: Точка є точкою дотикання Х тоді і тільки тоді, коли в будь-якому околі точки знайдуться точки множини Х.

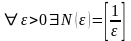
Довед: : . . Розглянемо послідовність околів . , яка належить , тоді розглянемо утв. нами посл-ть , 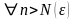бо . Отже, за озн.1 побудована нами