3.2.3 Метод хорд

Р

В качестве нового интервала для продолжения итерационного процесса выбираем из двух отрезков или тот, на концах которого функция f(x) принимает значения с разными знаками.

Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной погрешности

ассматриваемый метод так же, как и метод дихотомии, предназначен для уточнения корня на интервале [a, b], на концах которого левая часть решаемого уравнения f(x) принимает разные знаки. Интервал [а, b] по-прежнему определяем графическим методом, однако очередное приближение берем в отличие от метода дихотомии не в середине отрезка, а в точке х₁, где прямая линия, проведенная через точки f(a) и f(b), пересекает ось абсцисс (рис. 3.2).

погрешности _{, т. Е ,} или когда значения функции f(x) попадут в область шума, т. е. .

Уравнение прямой линии, проходящей через точки , запишем в общем виде: .

Коэффициенты k и с уравнения этой прямой определим из условий:

Вычитая левые и правые части последних соотношений, получим

Точку пересечения прямой y(x) с осью абсцисс получим, приравнивая y(x) к нулю:

(3.3)

или

.

(3.4)

3.2.4 Метод Ньютона (метод касательных)

Рассмотрим графическую иллюстрацию метода (рис. 3.3). Предположим, что графическим методом определено начальное приближение к корню. В точке вычислим левую часть решаемого уравнения f₀ = f(x₀)_, а также производную в этой точке . Следующее приближение к корню найдем в точке х₁, где касательная к функции f(х), проведенная из точки (x₀, f₀), пересекает ось абсцисс. Затем принимаем точку в качестве началь­ной и продолжаем итерационный процесс. Из графиков, приведенных на рис. 3.3, видно, что таким способом можно приближаться к корню . При этом с каждой итерацией расстояние между очередным и предыдущим приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выпол­нится условие:

_{, (3.5)}

где – допустимая погрешность определения корня.

Из геометрических соотношений (рис. 3.3, а) получим основную формулу метода Ньютона:

. (3.6)

В общем виде для k-го шага итерационного процесса соот­ношение (3.6) принимает вид:

. (3.7)

а б

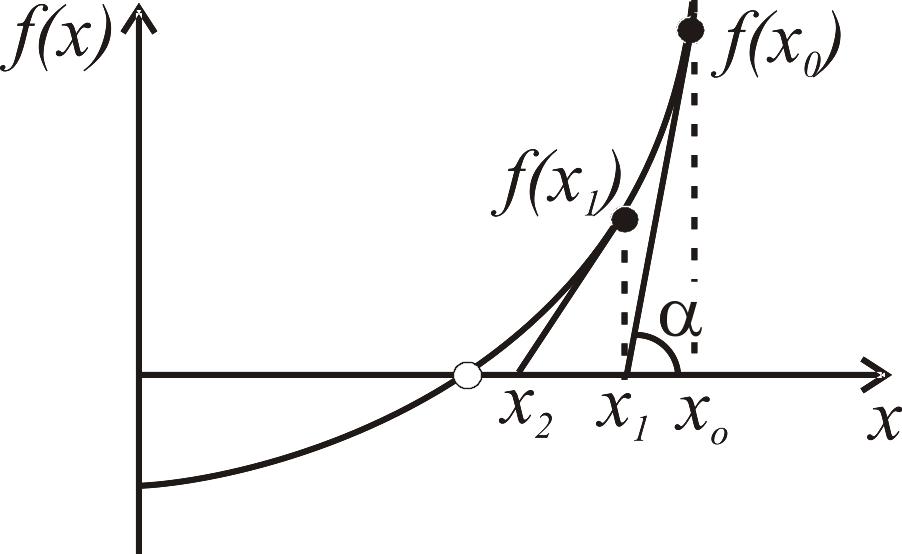
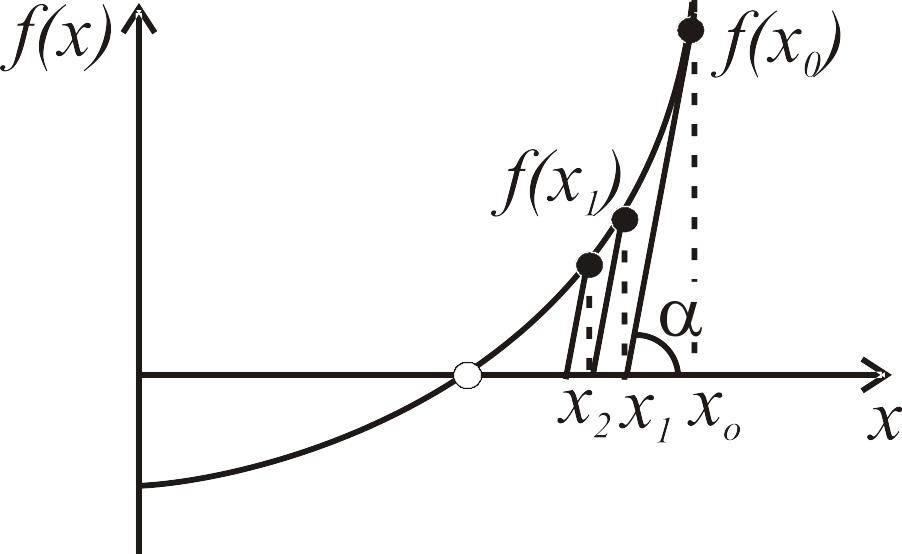
Рис. 3.3. Графическая иллюстрация метода Ньютона:

а – классический метод Ньютона; б – модифицированный метод Ньютона.

Алгоритм Ньютона можно получить другим способом с помощью раз­ложения в ряд Тейлора левой части уравнения f(x) вблизи корня . Итак, пусть , тогда и , так как .

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения ( – ) достигается через пять – шесть итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и ее производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычис­лением производной только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной . Получим алгоритм так назы­ваемого модифицированного метода Ньютона (рис. 3.3, б):

. (3.8)

Метод Ньютона (3.6) – (3.8) можно использовать для уточнения корней в области комплексных значений х, что необходимо при решении многих прикладных задач, в частности при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии. В этом случае начальное приближение к корню х₀ необходимо выбирать комплексным.

Обычно нет необходимости задавать полосу шума функции, так как по разности двух последующих приближений к корню можно оценивать сразу и значение отношения .