
- •7. Основы ВекторНой алгебры
- •7.1. Равенство векторов
- •7.2. Сложение векторов
- •Некоторые свойства:
- •7.10. Действия над векторами в координатной форме
- •7.10.1. На плоскости
- •7.10.2. В пространстве
- •8.2. Прямая линия на плоскости. Основные задачи
- •Кривые второго порядка
- •8.3.1. Окружность
- •8.3.2. Эллипс
- •Гипербола
- •Парабола
- •Уравнение прямой, проходящей через две точки
- •Параметрические уравнения прямой
- •Поверхности второго порядка. Их канонические уравнения
8.2. Прямая линия на плоскости. Основные задачи
|
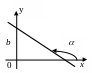
- уравнение прямой линии с угловым коэффициентом, где k = tg , - угол наклона прямой к положительному направлению оси Ох , b - величина отрезка, отсекаемого прямой на оси Оу |
|
- общее
уравнение
прямой линии на плоскости; здесь
Вектор
|
|
-
уравнение
прямой,
проходящей
через
данную
точку
|
Угол
, отсчитанный против часовой стрелки
от прямой
Для прямых, заданных уравнениями
формула (*) примет вид:
|
|
|
- условия параллельности прямых
или
|
|
- условия перпендикулярности прямых на плоскости. |
|
-
уравнение
прямой,
проходящей через две
данные точки:
|
|
- расстояние
от точки
до прямой
|
Кривые второго порядка
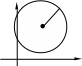
8.3.1. Окружность
|
R t |
|
|
|
R
A(a,b)
х 0 |
|
|

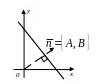

 y
y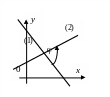
 y
y