7. Основы ВекторНой алгебры

7.1. Равенство векторов

Вектор равен вектору ( пишут ), если

они:

1) параллельны (коллинеарны),

2) сонаправлены (одного направления),

3) их длины равны :

7.2. Сложение векторов

		a) правило треугольника
		b) правило параллелограмма

7.3. Вычитание векторов

4. Умножение вектора на число

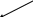
7.5. Скалярное произведение векторов

а) Определение:



2. Некоторые свойства:

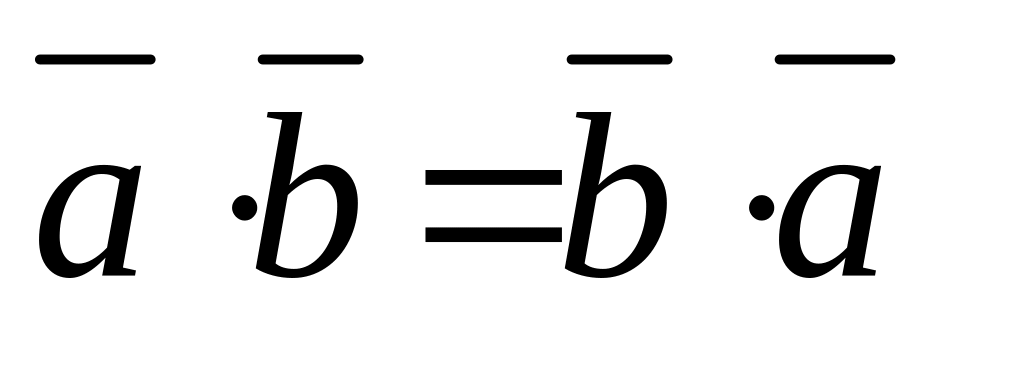• - переместительный закон ( коммутативный) справедлив;

• если , то

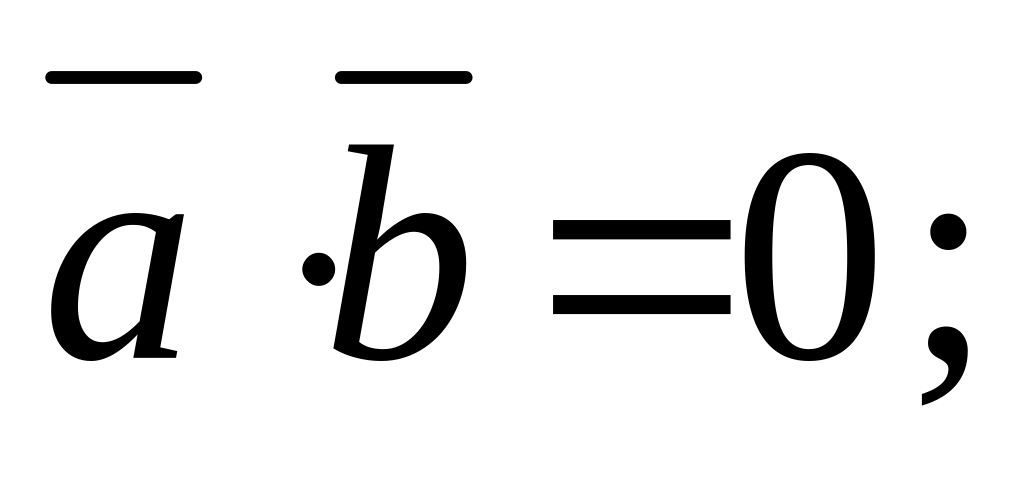
• если то 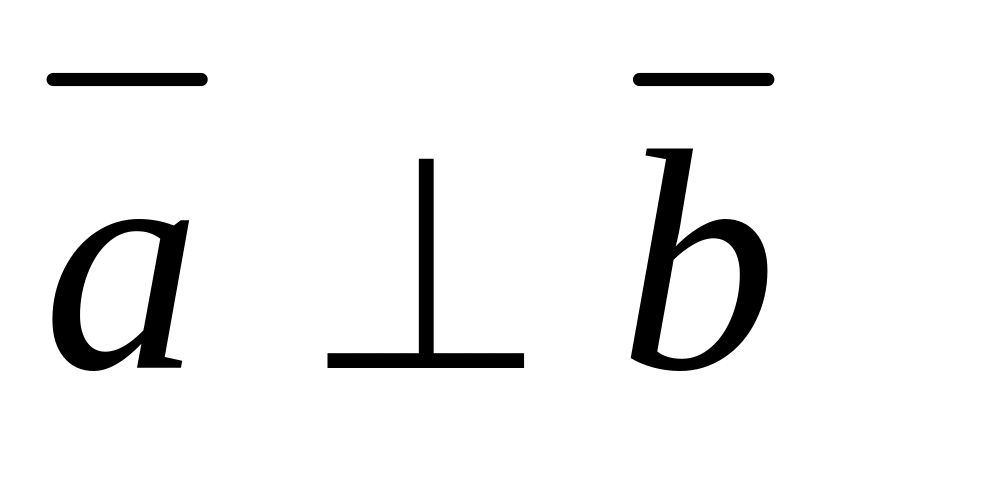(здесь ).

7.6. Векторное произведение ВЕКТОРОВ

а) Определение.

Векторным произведением векторов называют

вектор удовлетворяющий условиям:

1) ;

2) длина вектора численно равна площади параллелограмма, построенного на векторах и :

,

где - угол между векторами .

3) вектор направлен в ту сторону, что кратчайший поворот от вектора к вектору кажется происходящим против часовой стрелки, если смотреть с конца вектора .

Векторное произведение векторов обозначают различно:

2. Некоторые свойства:

   • ;

   • , k – число;

   • .

7.7. Двойное векторное произведение

есть вектор, компланарный (параллельный) векторам Вычисляется по формуле

В общем случае

7.8. Смешанное произведение трёх векторов

Обозначают различно: .

Е сли векторы ненулевые и некомпланарны, то смешанное произведение есть число, абсолютная величина которого равна объёму параллеле- пипеда, построенного на этих векторах, исходящих из

одной точки,

т.е. .

7.9. Векторы в координатной форме

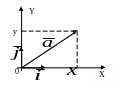
7.9.1. НА ПЛОСКОСТИ

		координатные единичные векторы (орты): где х, у - проекции вектора на оси координат (координаты вектора). Можно кратко писать: , ,
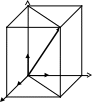
7.9.2. в пространстве
Z z 0 y Y x X	- координатные единичные векторы : . , где x, y, z - проекции вектора на оси координат. Вектор можно записать так: , или