
- •Специальные разделы математики для транспортных специальностей Сборник задач
- •Часть 1
- •Матрицы, определители и действия над ними
- •Матрицы и действия над ними. Справочный материал.
- •Задачи для самостоятельного решения.
- •1.2. Определители квадратных матриц. Справочный материал.
- •Задачи для самостоятельного решения.
- •1.3. Обратная матрица. Справочный материал.
- •Задачи для самостоятельного решения:
- •1.4. Ранг матрицы. Справочный материал.
- •Пример решения типового варианта.
- •2.2. Типовой расчет. Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
- •Вариант 21.
- •Вариант 22.
- •Вариант 28.
- •Вариант 29.
- •Векторное произведение векторов.
- •Смешанное произведение векторов.
- •4.2. Аналитическая геометрия в пространстве.
- •4.2.1. Плоскость.
- •4.2.2. Прямая линия в пространстве.
- •4.2.3. Прямая линия и плоскость в пространстве.
- •Задачи для самостоятельного решения.
- •Пример решения типового расчета.
- •4.3. Типовой расчет:
- •5. Линейное программирование
- •5.1 Постановка задач линейного программирования
- •Геометрический метод решения задач линейного программирования
- •Программирования симплекс – методом
- •Метод искусственного базиса
- •5.5. Элементы теории двойственности в линейном программировании
- •Модифицированный симплекс-метод (метод обратной матрицы)
- •Задачи для самостоятельного решения
- •Привести данные задачи к форме основной задачи лп:
- •Решение типового варианта
- •5.9. Типовой расчет
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •6. Литература
- •Оглавление
- •1. Матрицы, определители и действия над ними
- •1.1. Матрицы и действия над ними
- •Специальные разделы математики для транспортных специальностей
- •Часть 1
- •190031, СПб., Московский пр., 9.
Пример решения типового варианта.
Задание №1.
Для данных матриц
![]() ,
,
![]() и
и
![]()
Найти:
1.
![]() .
.
2.
![]() .
.
Решение:
Транспонируем матрицу :
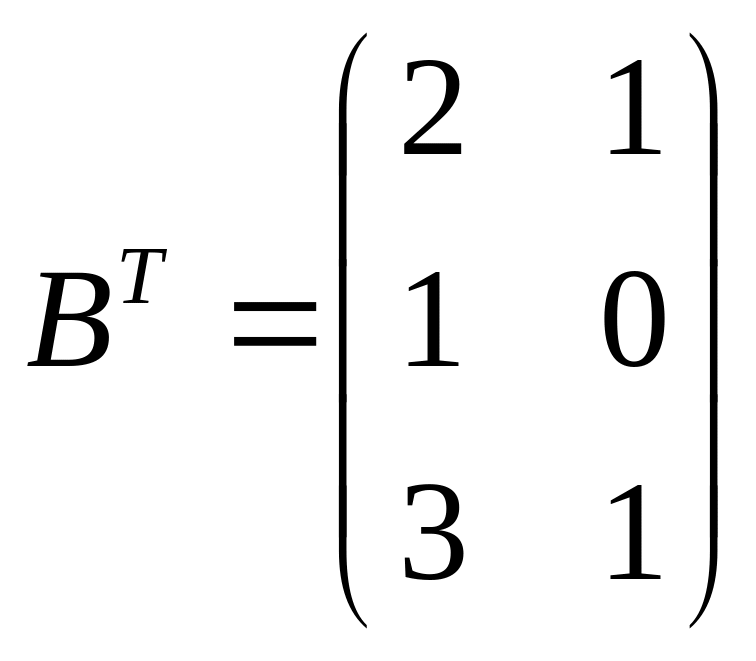 .
.
Найдем
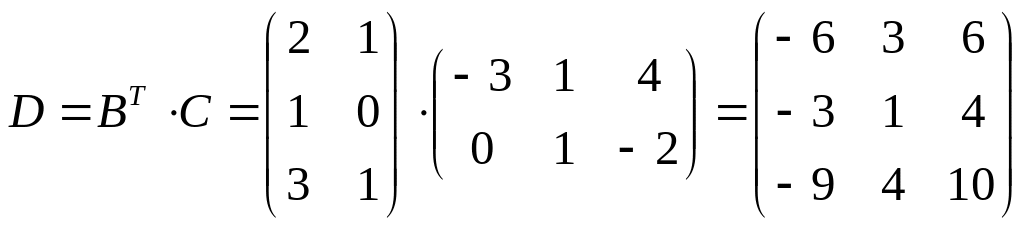 ,
,
в частности элемент
![]()
Ответ:
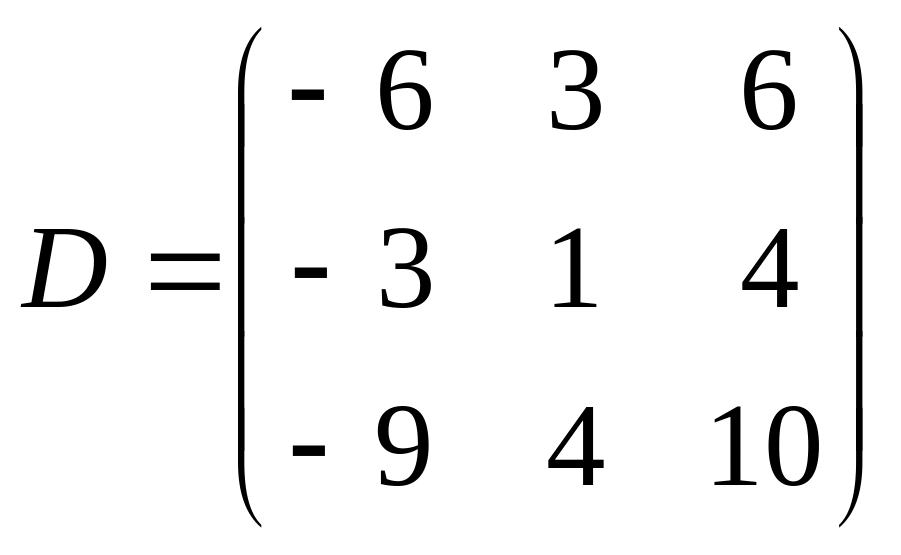 .
.
Матрица - невырожденная, так как
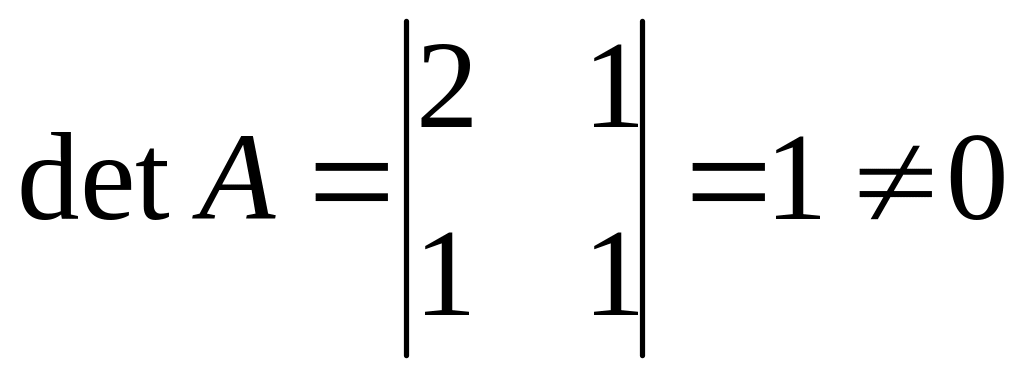 .
.
Обратную матрицу
находим по формуле:
![]() .
.
Найдем алгебраические дополнения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Запишем
![]() .
.
Вычислим
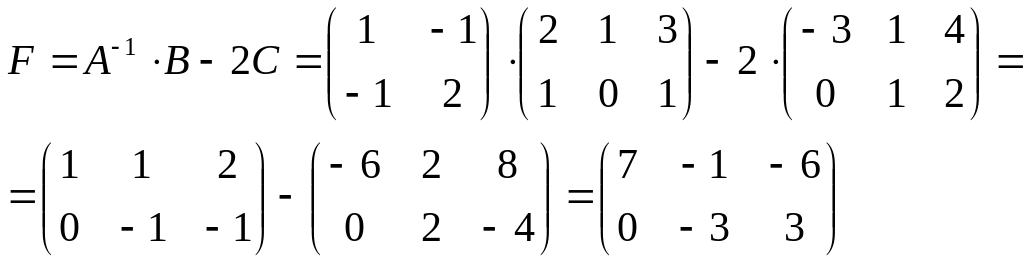 .
.
Ответ:
![]()
Задание №2.
Вычислить определитель, используя его свойства:
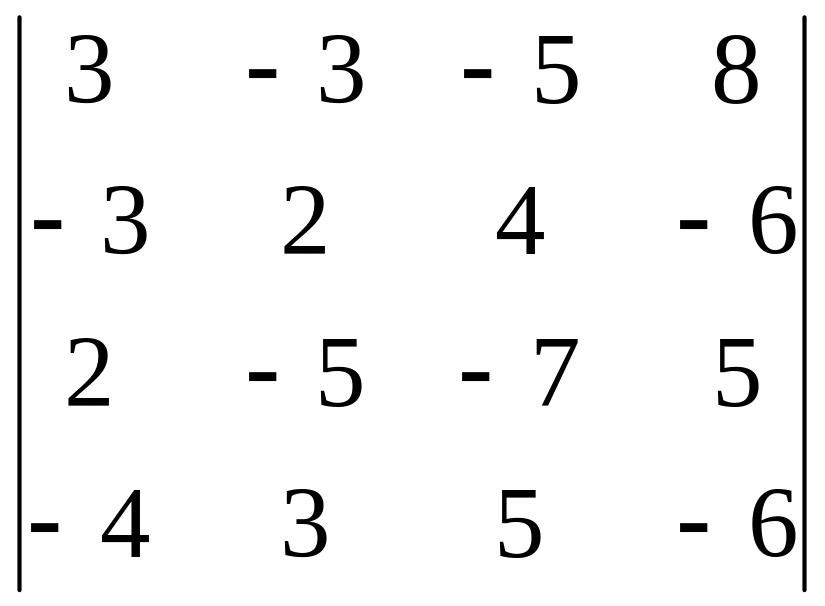 .
.
Решение:
Известно, что определитель матрицы n – го порядка может быть разложен по элементам любой строки (столбца).
В частности верна формула:
![]() ,
(1)
,
(1)
где k
– номер
строки, по которой ведется разложение;
![]() - алгебраические дополнения соответствующих
элементов.
- алгебраические дополнения соответствующих
элементов.
Разложим данный определитель по элементам 1 – ой строки:
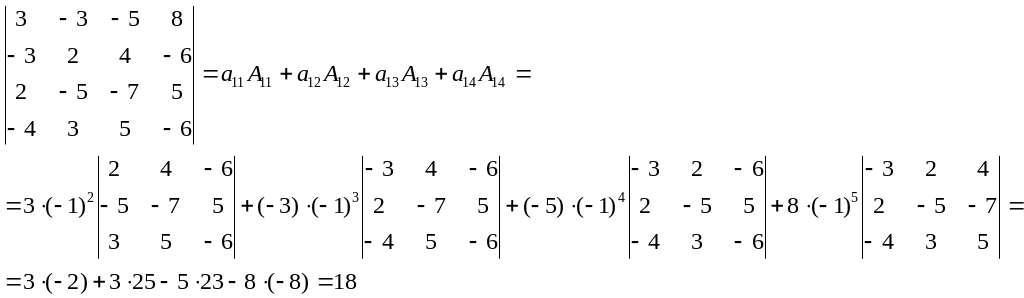 (Определители
третьего порядка вычислены по правилу
треугольников.)
(Определители
третьего порядка вычислены по правилу
треугольников.)
Объем вычислений
может быть уменьшен, если в строке
(столбце), по которой ведется разложение,
есть элементы равные нулю (т. к.
![]() ).
).
При вычислении определителя n – го порядка используют следующие методы:
Метод понижения порядка.
Используя свойства определителя, его преобразуют так, чтобы все элементы некоторого ряда1, кроме одного, стали равны нулю, а затем раскладывают определитель по этому ряду. При этом разложение будет содержать только один определитель (n-1) – го порядка, к которому применяют тот же прием.
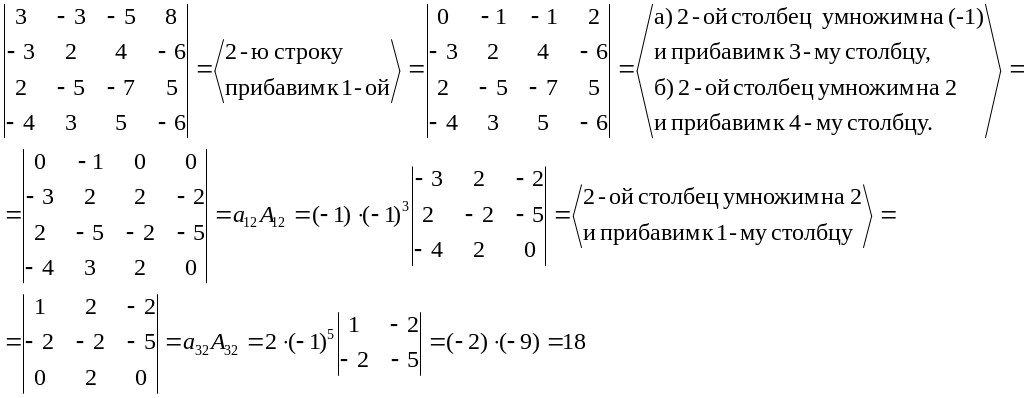
Сведение определителя к треугольному виду:
Определитель преобразуется так, чтобы все элементы, лежащие по одну сторону от главной диагонали, стали равными нулю.

Таким образом определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
Задание №3.
Решить систему линейных уравнений:
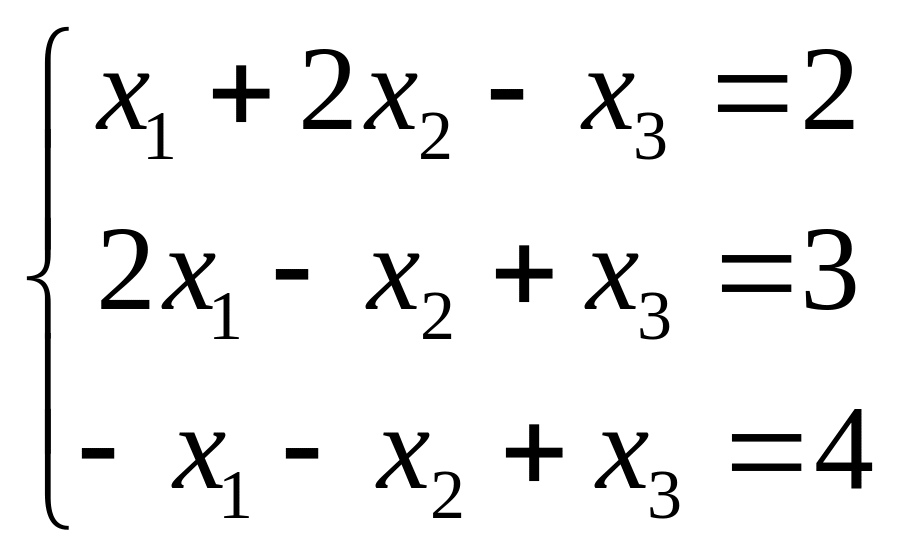 (1)
(1)
с помощью обратной матрицы.
по формулам Крамера.
методом Гаусса.
Решение:
1. Заметим, что дана система, у которой число уравнений равно числу неизвестных.
Запишем систему (1) в матричной форме:
, (2)
где
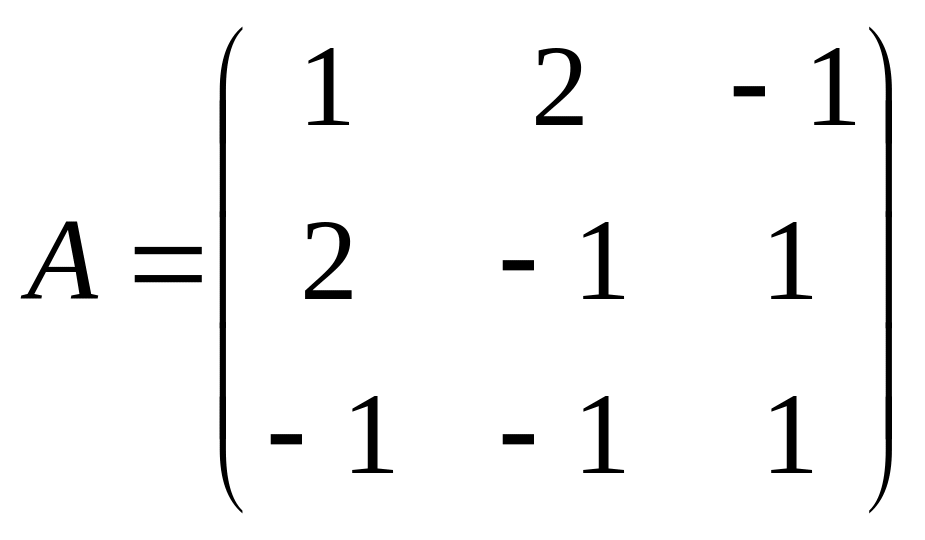 ,
,
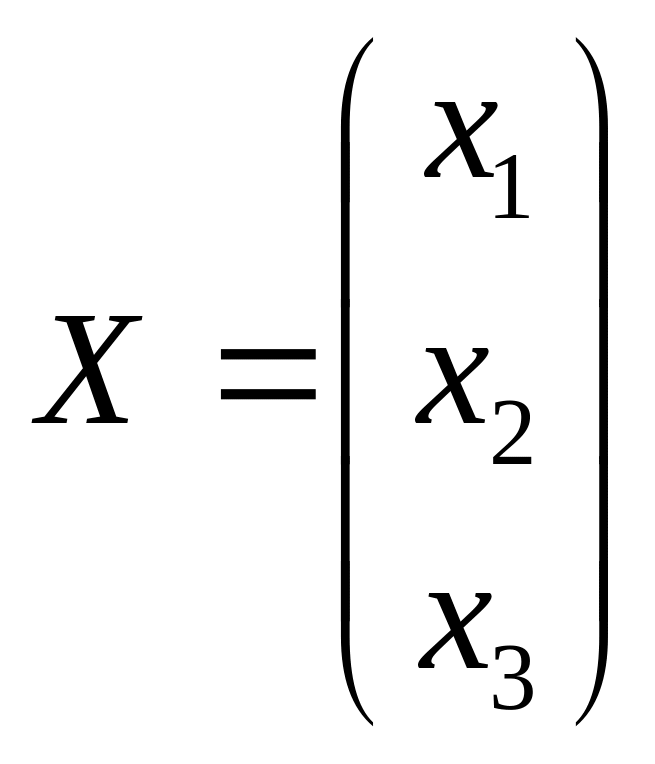 ,
,
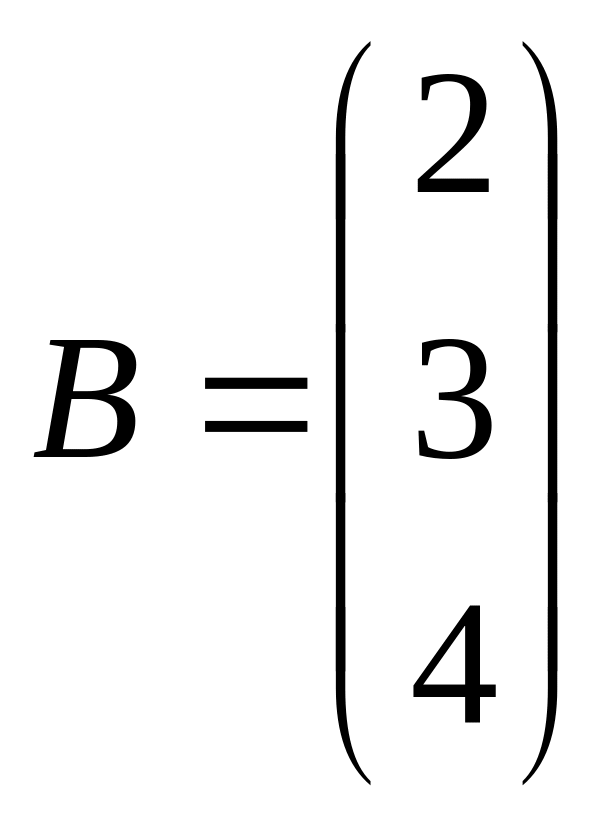
Если в системе
(1)
![]() ,
то матрица
имеет единственную обратную
,
то матрица
имеет единственную обратную
![]() .
.
В этом случае решение системы находится по формуле:
(3).
Вычислим определитель матрицы :
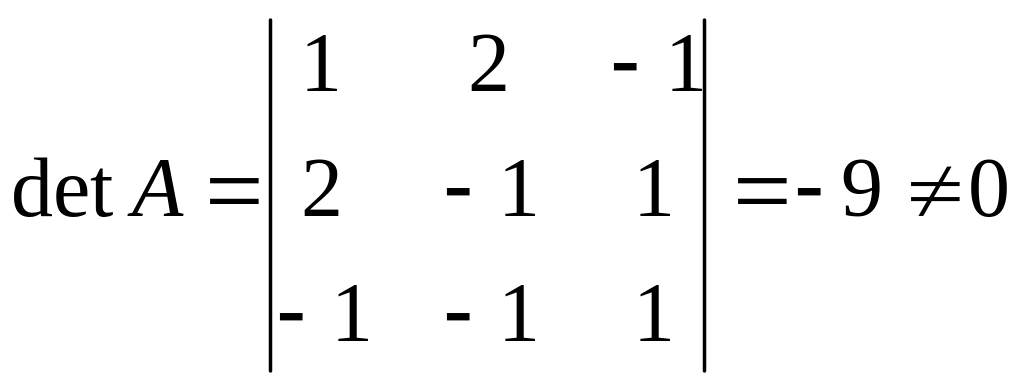 ,
так как
,
так как
![]() ,
то матрица
имеет обратную
.
,
то матрица
имеет обратную
.
Для построения матрицы вычислим алгебраические дополнения элементов матрицы :

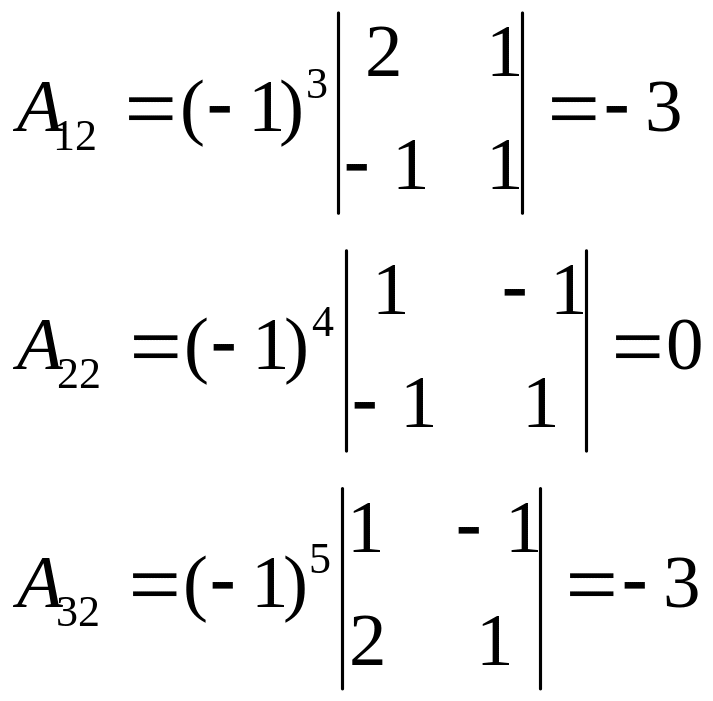
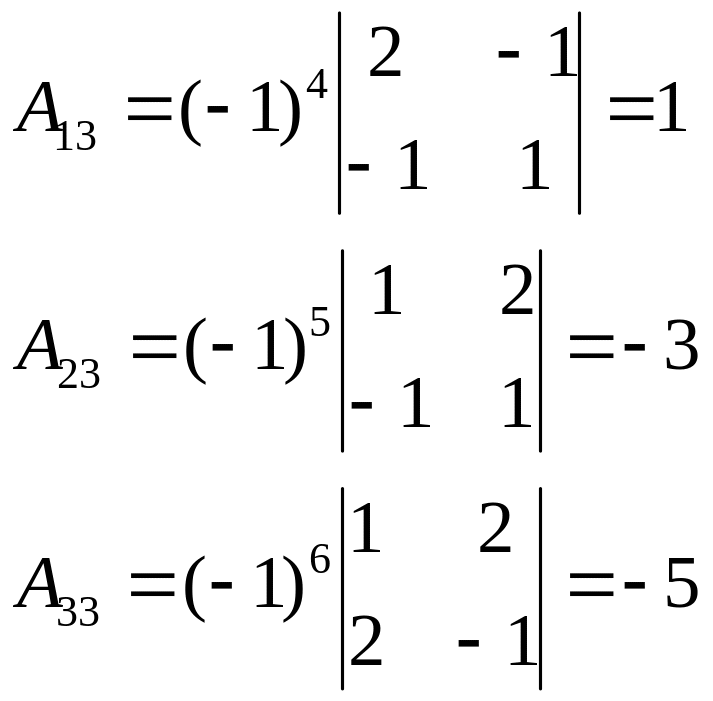
Найдем обратную матрицу :
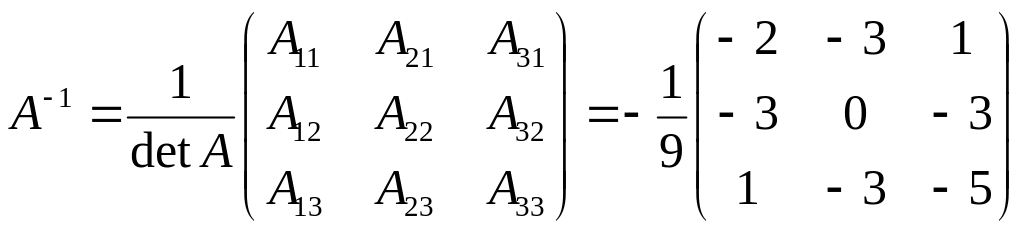 .
.
Согласно формуле (3) решение системы имеет вид:
 ,
,
то есть
![]() .
.
Ответ:
![]() .
.
2. По формулам Крамера решение системы находится следующим образом:
![]() (
(![]() ),
),
![]() ,
(4)
,
(4)
где
![]() - определитель, получающийся из
определителя системы, заменой
- го столбца на столбец свободных членов.
- определитель, получающийся из
определителя системы, заменой
- го столбца на столбец свободных членов.
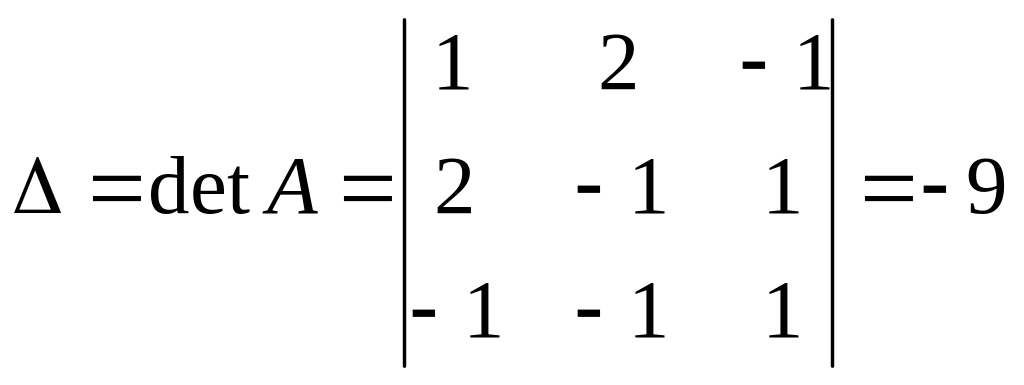 (найден в п.1).
(найден в п.1).
Так как , то система имеет единственное решение.
Вычислим вспомогательные определители:
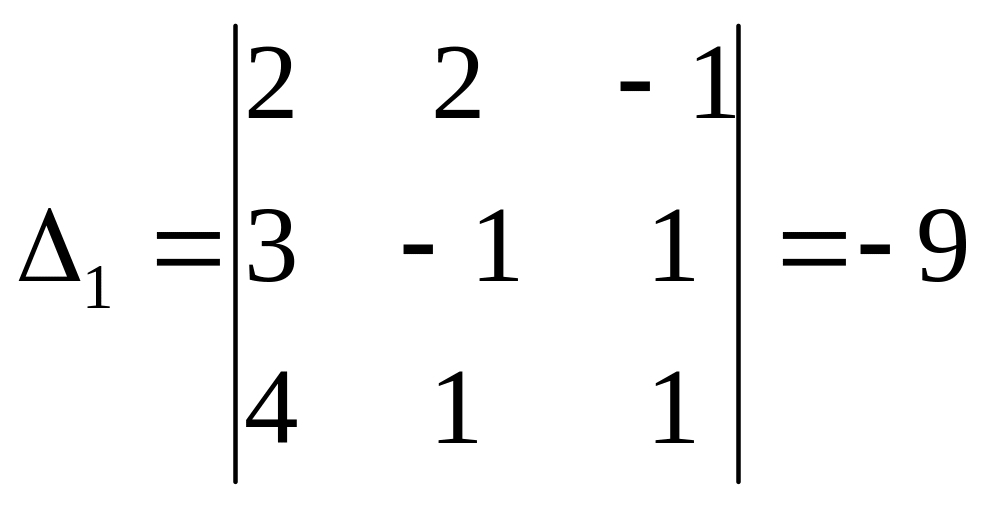 ,
,
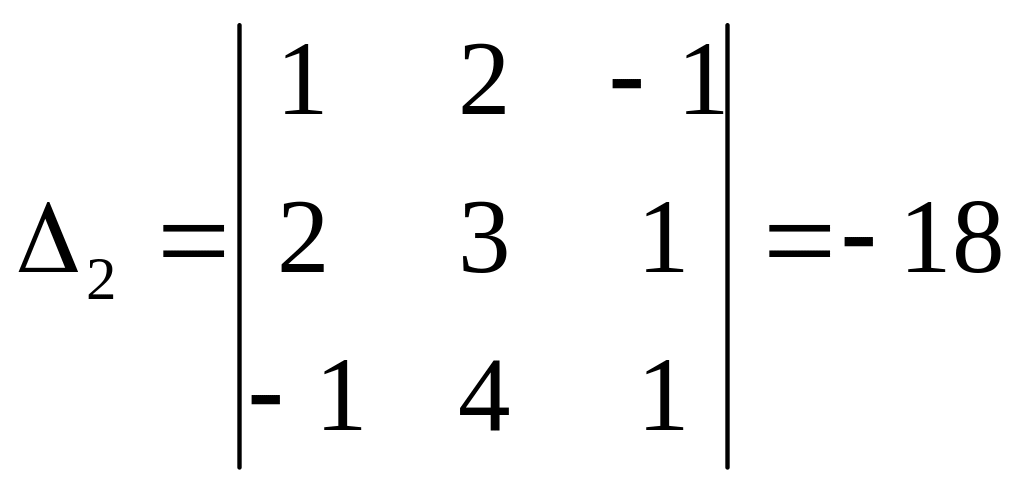 ,
,
 .
.
Согласно формуле (4), определяем решение системы:
![]() ,
,
![]() ,
,
![]() .
.
Ответ:
![]() .
.
3. Метод Гаусса – состоит в последовательном исключении неизвестных.
Составим расширенную
матрицу системы, приписав справа к
матрице системы столбец свободных
членов:
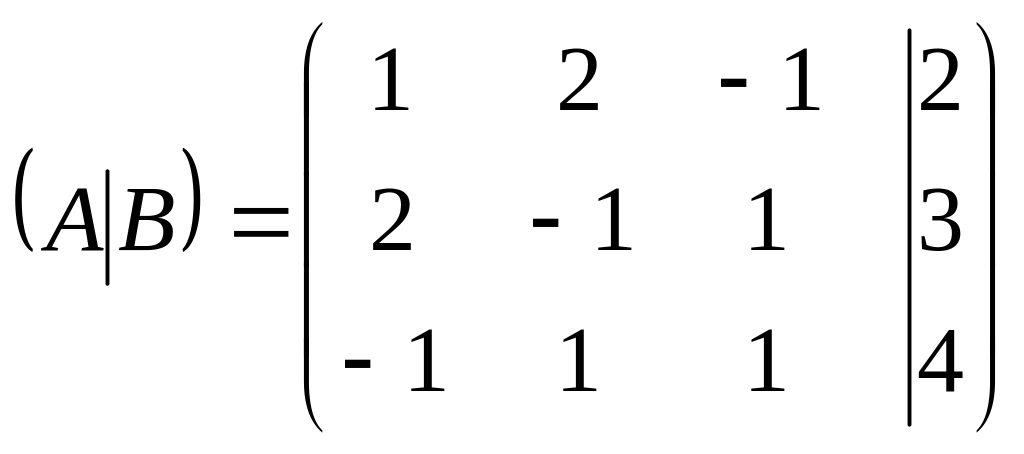 .
.
Проводя элементарные преобразования над строками этой матрицы, сведем ее к трапециевидному (в частности, треугольному) виду:
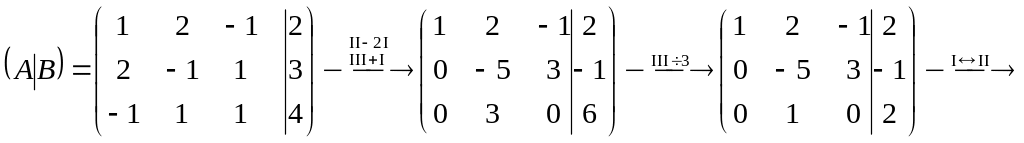
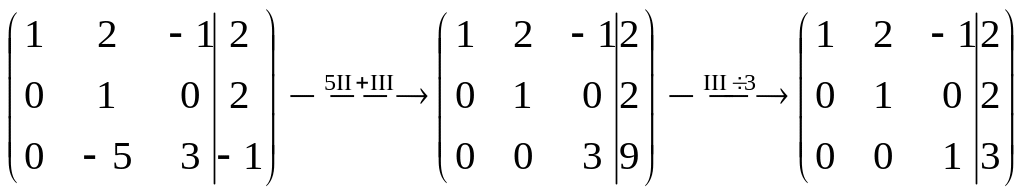 .
.
Последняя матрица
является расширенной матрицей системы
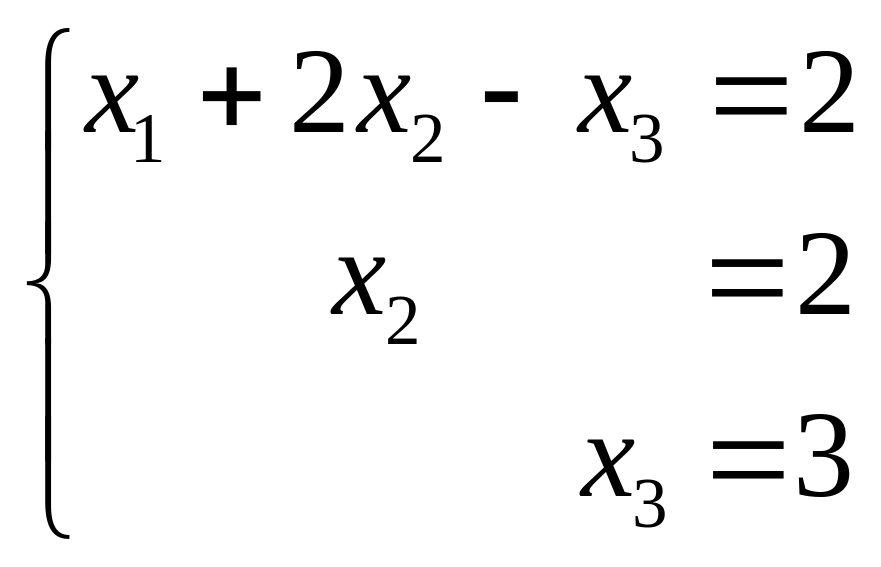 ,
которая эквивалентна исходной. Этот
этап называется прямым ходом метода
Гаусса.
,
которая эквивалентна исходной. Этот
этап называется прямым ходом метода
Гаусса.
Осуществив обратный ход метода Гаусса, прочитав систему снизу вверх, получим решение системы:
![]() .
.
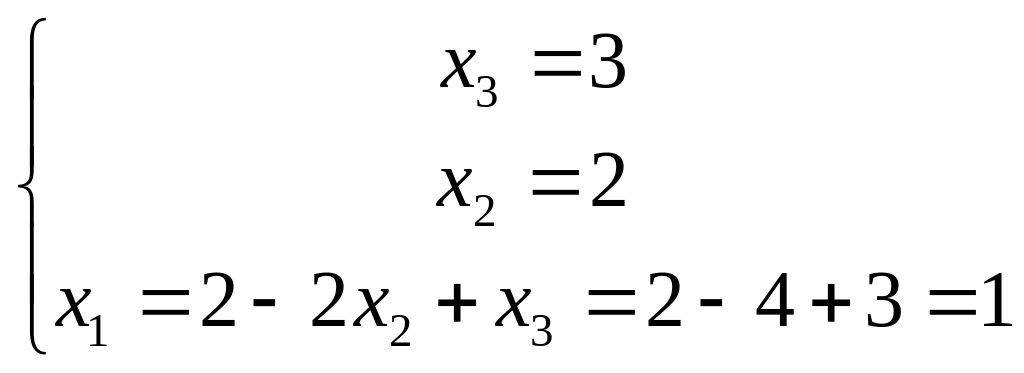
Ответ:
Замечание: Заметим, что наиболее важным при решении систем, является метод Гаусса, так как им можно решать и системы, у которых m≠n и который позволяет однозначно установить, является ли данная система определенной, неопределенной или несовместной.
Задание №4.
При каком значении однородная система имеет ненулевое решение. Найти все решения системы при найденном :
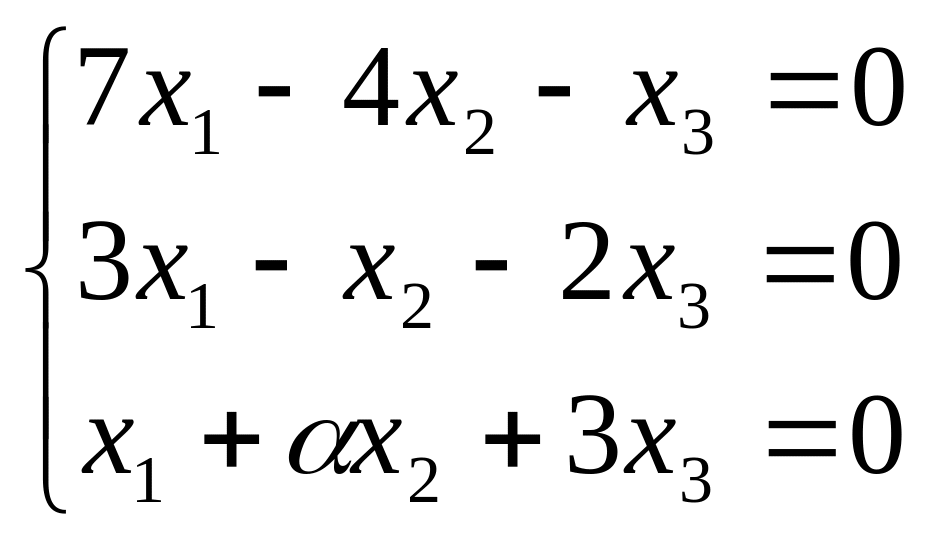 (1)
(1)
Дана однородная
система у которой число уравнений равно
числу неизвестных. Эта система (1) имеет
ненулевое решение тогда и только тогда,
когда определитель матрицы системы
равен нулю
![]() .
Из этого условия находим коэффициент
.
.
Из этого условия находим коэффициент
.
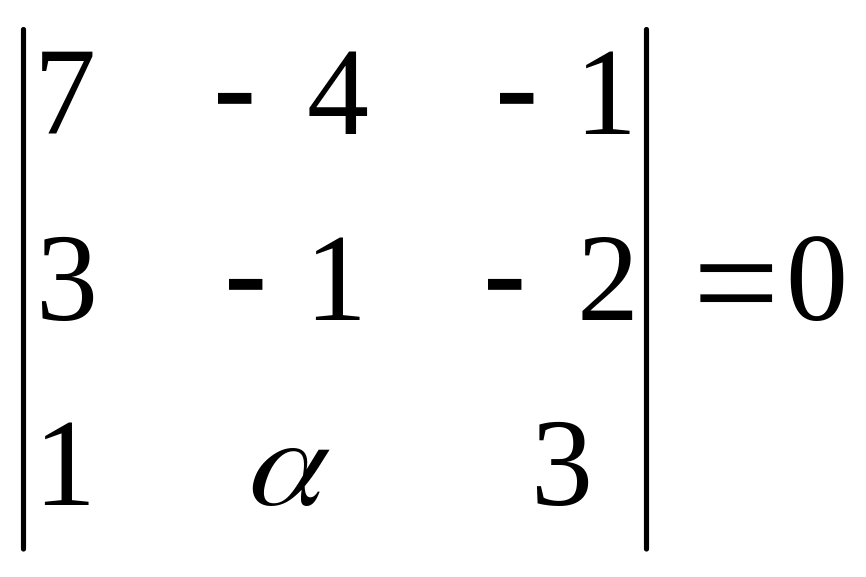
Раскладывая определитель по элементам третьей строки, получаем:
![]() или
или
![]() ,
следовательно
,
следовательно
![]() и
и
![]() .
.
Подставляем в заданную систему.
Получим:
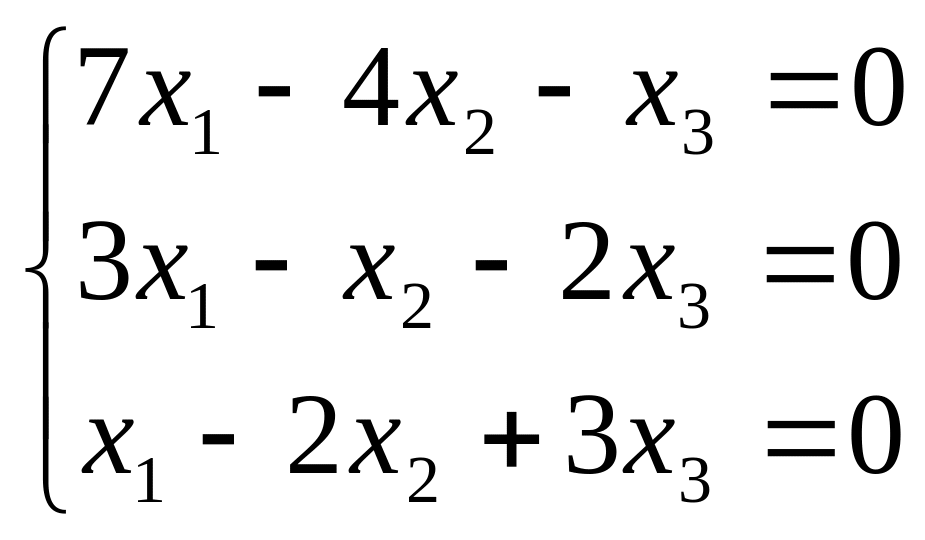
Решим полученную систему методом Гаусса:
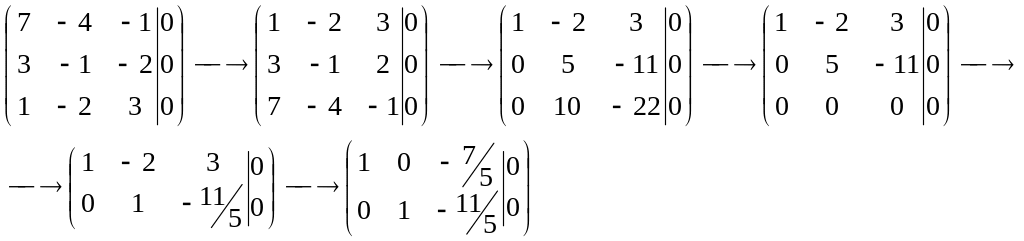
Последняя расширенная
матрица соответствует новой системе:
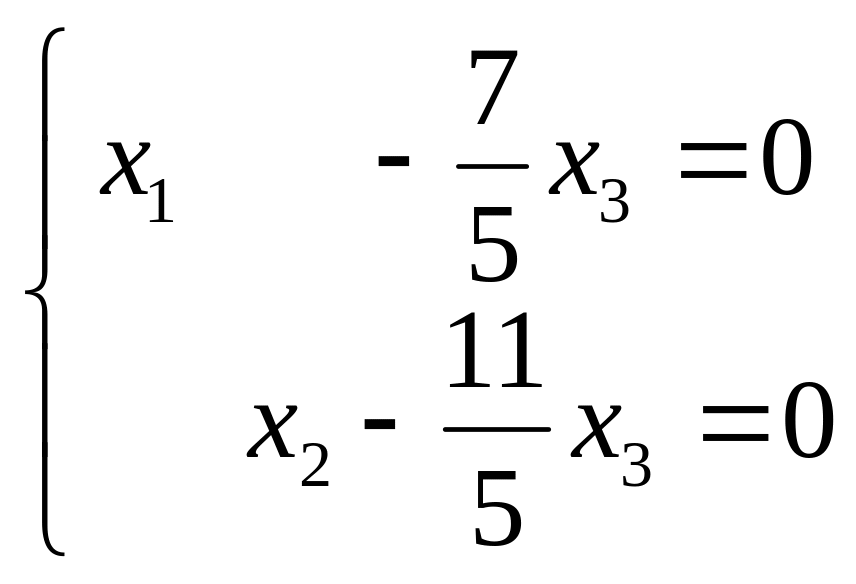 , которая равносильна исходной системе.
, которая равносильна исходной системе.
Считая
![]() и
и
![]() - базисными переменными, а
- базисными переменными, а
![]() - свободной, можем записать множество
решений исходной системы в виде:
- свободной, можем записать множество
решений исходной системы в виде:
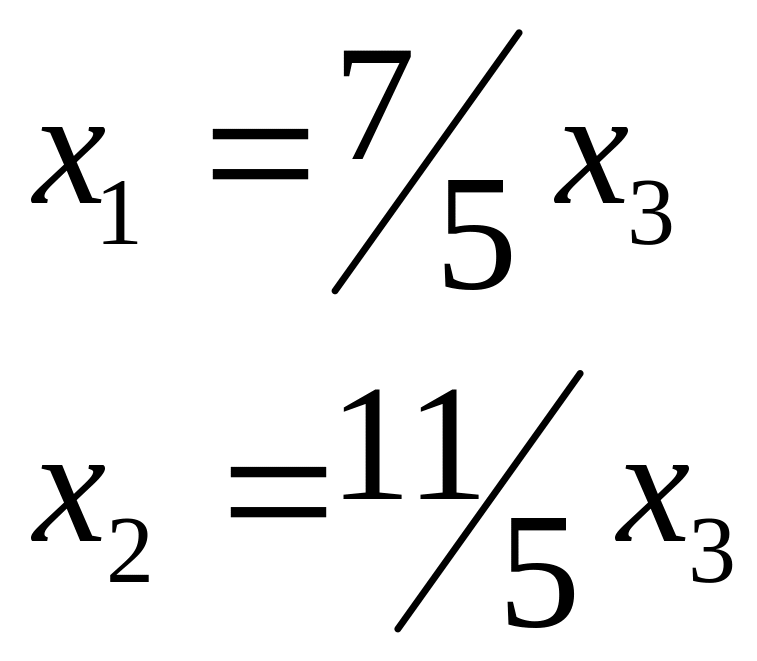 ,
где
,
где
![]() - любое вещественное число. Таким
образом система имеет бесчисленное
множество решений.
- любое вещественное число. Таким
образом система имеет бесчисленное
множество решений.
.
Задание №5.
Найти ранг матрицы
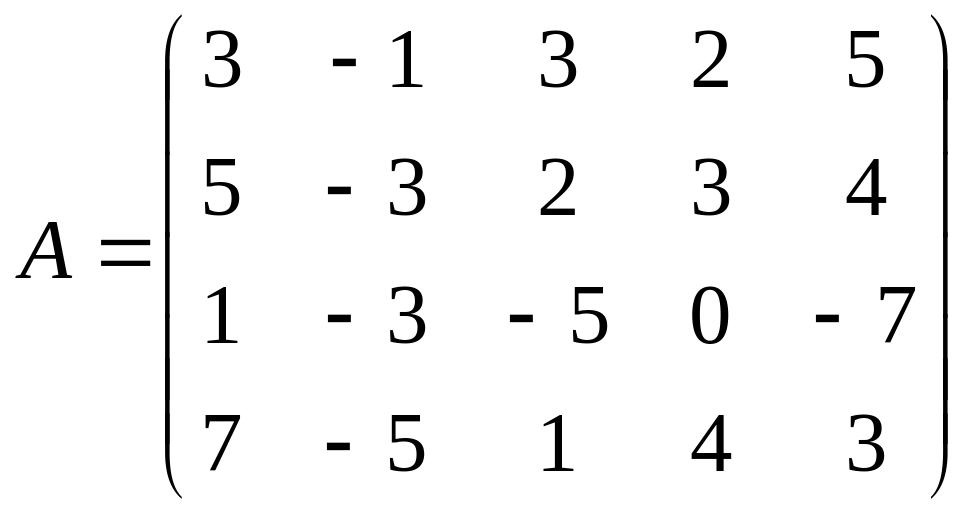 и указать один из базисных миноров.
и указать один из базисных миноров.
Решение:
Так как элементарные преобразования не меняют ранга матрицы, а ранг ступенчатой матрицы равен числу ее ненулевых строк, то для нахождения ранга матрицы надо:
Свести исходную матрицу к ступенчатому виду.
Подсчитать число ненулевых строк в ступенчатой матрице.

Матрица сведена
к ступенчатому виду. Число ее ненулевых
строк равно двум, следовательно
![]() .
.
Замечание: вычисляя ранг матрицы можно преобразовывать как строки, так и столбцы матрицы.
Задание №6.
Исследовать системы линейных уравнений с помощью теоремы Кронекера – Капелли и в случае совместности решить их.
1.
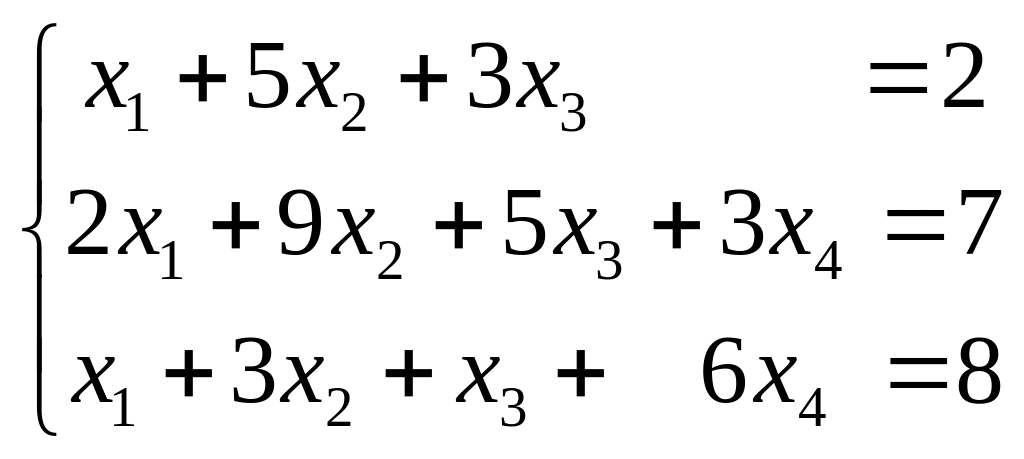 ,
2.
,
2.
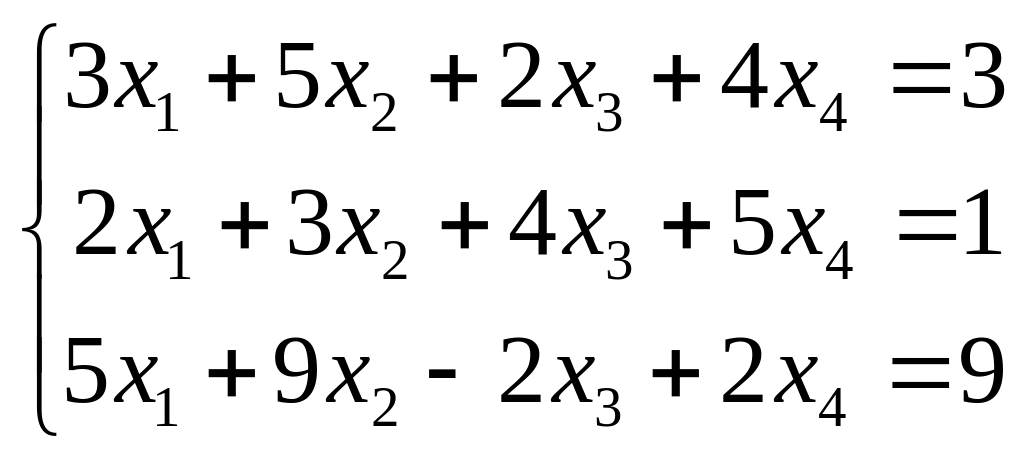
Решение:
Определим ранг матрицы системы и расширенной матрицы.
Для этого выпишем расширенную матрицу системы, и с помощью линейных преобразований над строками, сведем ее к ступенчатому виду.
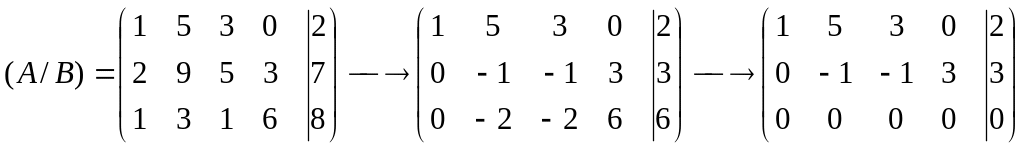
Таким образом ранги расширенной и основной матриц системы равны:
![]() .
.
Число неизвестных
в данной системе
![]() ,
т. е.
,
т. е.
![]() .
.
В силу теоремы Кронекера – Капелли система совместна и имеет бесчисленное множество решений (т.е. система является неопределенной).
Выпишем систему равносильную исходной:
![]() (*)
(*)
![]() -
базисный минор(составлен из коэффициентов
при неизвестных
-
базисный минор(составлен из коэффициентов
при неизвестных
![]() ).
).
Выбор базисного минора определяет базисные переменные (их число равно r). Остальные неизвестные, число которых (n – r) называются свободными.
В
системе (*): базисные переменные -
![]() ,
,
свободные
переменные -
![]() .
.
Чтобы
найти общее решение системы, надо
выразить базисные переменные через
свободные. «Обратным ходом» метода
Гаусса из последнего уравнения системы
(*), получаем:
![]() ,
тогда
,
тогда
![]() .
.
Задавая
свободным переменным произвольные
значения
![]() запишем общее решение системы в виде:
запишем общее решение системы в виде:
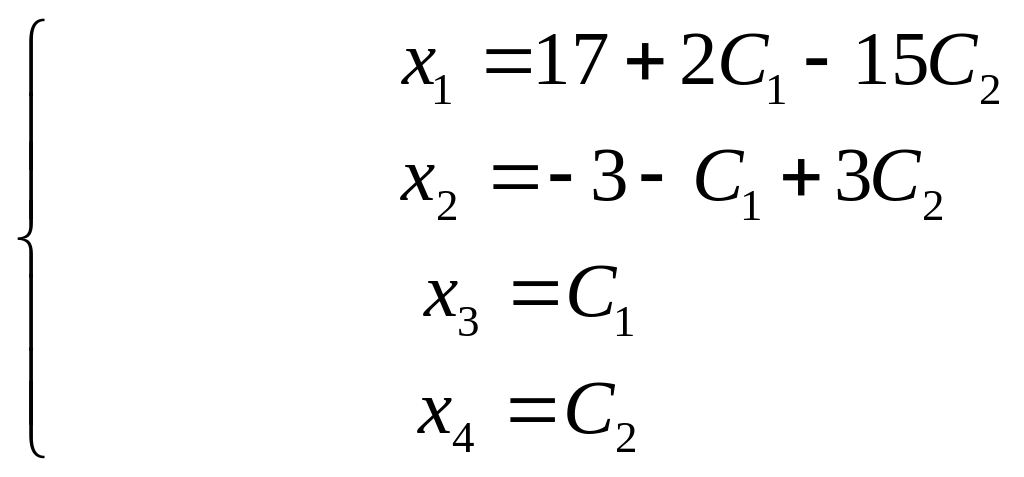 .
.
Проведем элементарные преобразования над строками расширенной матрицы системы:
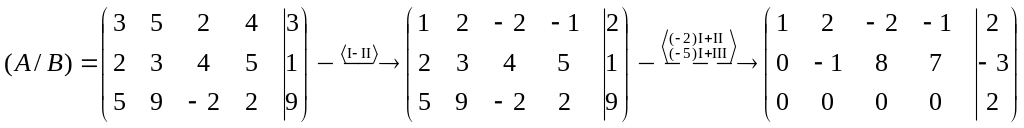
Итак
![]() ,
следовательно
,
следовательно
![]() ,
т.е. система несовместна (не имеет
решений).
,
т.е. система несовместна (не имеет
решений).
Замечание: При решении системы уравнений при m<n (число уравнений меньше числа неизвестных) нужно уметь разбивать переменные, заданной системы уравнений на основные и свободные. Находить любое возможное решение системы, имеющей хотя бы одну группу основных переменных.
А так же необходимо знать и уметь объяснить, какие системы уравнений называются совместными (определенными и неопределенными) и несовместными.
