
- •Специальные разделы математики для транспортных специальностей Сборник задач
- •Часть 1
- •Матрицы, определители и действия над ними
- •Матрицы и действия над ними. Справочный материал.
- •Задачи для самостоятельного решения.
- •1.2. Определители квадратных матриц. Справочный материал.
- •Задачи для самостоятельного решения.
- •1.3. Обратная матрица. Справочный материал.
- •Задачи для самостоятельного решения:
- •1.4. Ранг матрицы. Справочный материал.
- •Пример решения типового варианта.
- •2.2. Типовой расчет. Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 19.
- •Вариант 20.
- •Вариант 21.
- •Вариант 22.
- •Вариант 28.
- •Вариант 29.
- •Векторное произведение векторов.
- •Смешанное произведение векторов.
- •4.2. Аналитическая геометрия в пространстве.
- •4.2.1. Плоскость.
- •4.2.2. Прямая линия в пространстве.
- •4.2.3. Прямая линия и плоскость в пространстве.
- •Задачи для самостоятельного решения.
- •Пример решения типового расчета.
- •4.3. Типовой расчет:
- •5. Линейное программирование
- •5.1 Постановка задач линейного программирования
- •Геометрический метод решения задач линейного программирования
- •Программирования симплекс – методом
- •Метод искусственного базиса
- •5.5. Элементы теории двойственности в линейном программировании
- •Модифицированный симплекс-метод (метод обратной матрицы)
- •Задачи для самостоятельного решения
- •Привести данные задачи к форме основной задачи лп:
- •Решение типового варианта
- •5.9. Типовой расчет
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •6. Литература
- •Оглавление
- •1. Матрицы, определители и действия над ними
- •1.1. Матрицы и действия над ними
- •Специальные разделы математики для транспортных специальностей
- •Часть 1
- •190031, СПб., Московский пр., 9.
1.3. Обратная матрица. Справочный материал.
Квадратная матрица
 называется обратной для квадратной
матрицы
того же порядка, если
называется обратной для квадратной
матрицы
того же порядка, если
![]() ,
(1)
,
(1)
где Е – единичная матрица того же порядка, что и матрица А.
Квадратная матрица называется невырожденной (или неособенной), если ее определитель отличен от нуля, т.е.
 .
.Обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная, т. е. .
В этом случае ее можно найти по формуле:
![]() ,
,
где
![]() - присоединенная матрица, элементы
которой
- присоединенная матрица, элементы
которой![]() равны алгебраическим дополнениям
элементов матрицы
равны алгебраическим дополнениям
элементов матрицы
![]() ,
транспонированной к матрице
,
т.е.
,
транспонированной к матрице
,
т.е.
 .
.
Примеры:
Выяснить, является ли матрица
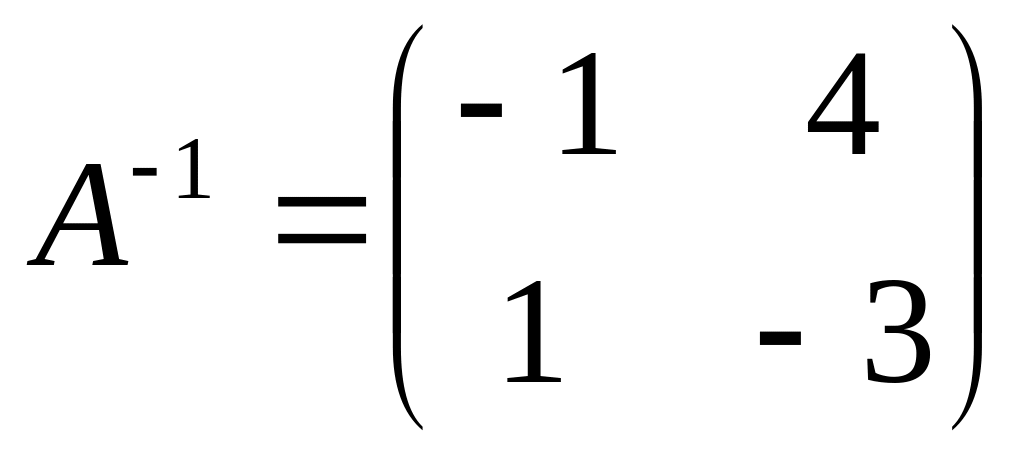 обратной к матрице
обратной к матрице
 .
.
Решение:
Найдем произведения
![]() .
.
![]()
![]()
В соответствии с определением (1) данные матрицы являются взаимно обратными.
Определить, имеют ли данные матрицы обратные:
 .
.
Решение:
Матрица
обратной не имеет, т. к. она не квадратная
(ее размер
![]() ).
).
Матрица
имеет обратную, т. к. ее определитель
 .
.
Матрица
![]() обратной не имеет, т. к. определитель
этой матрицы
обратной не имеет, т. к. определитель
этой матрицы

![]() .
.
Найти матрицу, обратную к данной
 .
.
Решение:
Найдем определитель матрицы :
 .
.
Так как , следовательно, матрица имеет обратную.
Напомним, что обратная матрица вычисляется по формуле:
 ,
(1)
,
(1)
где
![]() алгебраические дополнения элементов
алгебраические дополнения элементов
![]() матрицы
.
матрицы
.
Найдем алгебраические дополнения элементов матрицы :

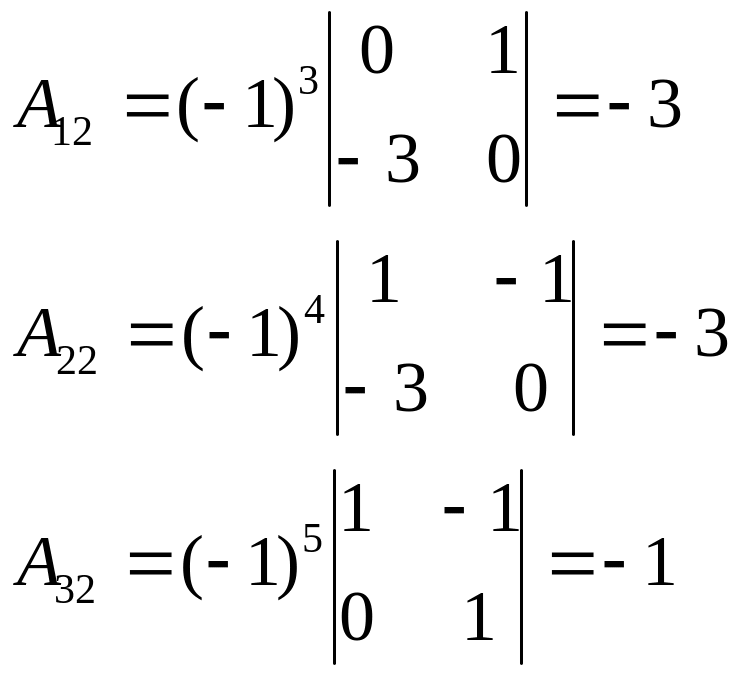

Находим обратную матрицу по формуле (1):
 .
.
Проверим правильность вычисления обратной матрицы:

Задачи для самостоятельного решения:
Вычислить, какие из приведенных матриц имеют обратные.
 .
. .
. .
. .
.
Для следующих матриц найти обратные:
 .
. .
. .
.
Решить матричные уравнения:

 .
.
Указание: Х – квадратная матрица второго порядка.
Исходное
матричное уравнение имеет вид
![]() .
.
Для нахождения матрицы Х достаточно умножить обе части исходного
уравнения
на
слева
![]() .
.
Выполнить действия
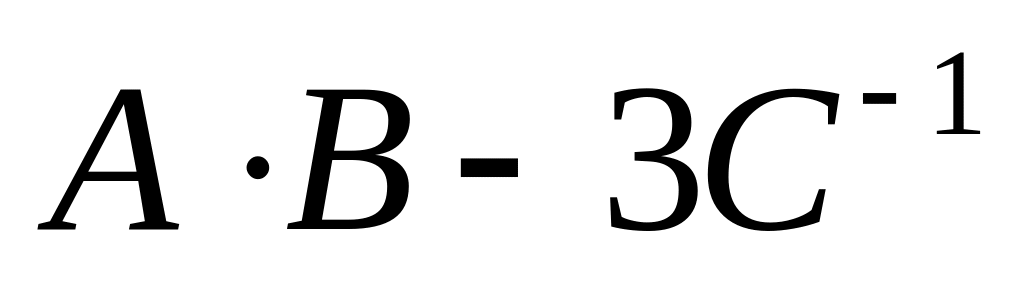 ,
где
,
где
 .
.Найти матрицу , обратную к матрице
 ,
где
,
где
 ,
,
 .
.
1.4. Ранг матрицы. Справочный материал.
Рангом матрицы
 или
или
 называется
максимальный порядок отличных от нуля
миноров этой матрицы.
называется
максимальный порядок отличных от нуля
миноров этой матрицы.
Ранг прямоугольной матрицы
 удовлетворяет неравенству:
удовлетворяет неравенству:
![]() .
.
Если матрица - квадратная порядка , то
 тогда и только тогда, когда
тогда и только тогда, когда
 .
.
Элементарные преобразования, не меняющие ранга матрицы
Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
Прибавление к элементам какой либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на некоторое число
Перестановка двух строк (столбцов) матрицы.
Транспонирование матрицы.
Отбрасывание нулевой строки (столбца).
С помощью элементарных преобразований матрицу
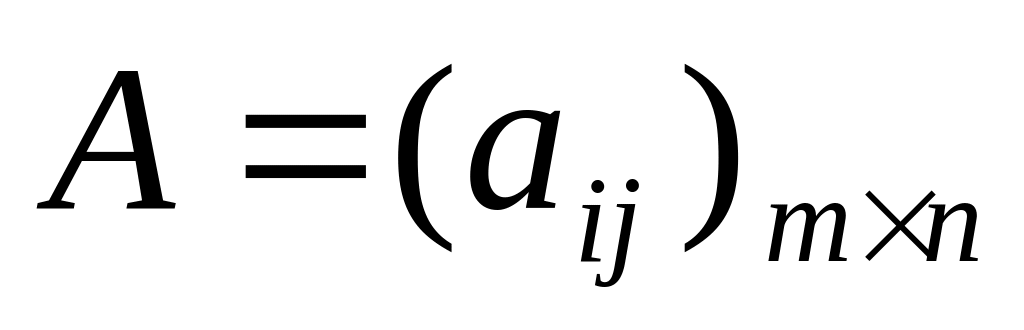 приводят
к ступенчатому виду:
приводят
к ступенчатому виду:
 ,
где
,
где
все
диагональные элементы
![]() ,
отличные от нуля, а элементы, расположенные
ниже диагональных элементов равны нулю.
,
отличные от нуля, а элементы, расположенные
ниже диагональных элементов равны нулю.
Так как минор
 ,
то ранг ступенчатой матрицы
равен
,
то ранг ступенчатой матрицы
равен
![]()
(т.е. числу ненулевых строк ступенчатой матрицы B).
Базисный минор – это не равный нулю минор, порядок которого равен рангу матрицы. Матрица может иметь несколько базисных миноров.
Пример.
Найти ранг матрицы и указать один из базисных миноров.

Решение:
матрица имеет размер
![]() ,
,
![]() ,
значит
,
значит
![]() .
.
С помощью элементарных преобразований приведем матрицу к ступенчатому виду.

Получили ступенчатую матрицу, у которой две ненулевые строки.
Таким образом ранг исходной матрицы А равен двум.
Выделенный минор может быть выбран в качестве базисного.
Задачи для самостоятельного решения:
Найти с помощью элементарных преобразований ранг матрицы:
1.
 2.
2.
 3.
3.
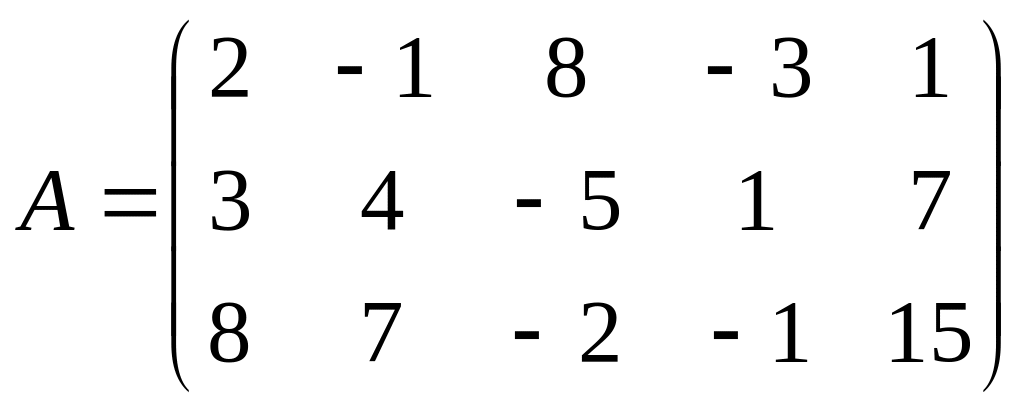
4.
 5.
5.
 6.
6.
 .
.
2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
2.1. Общий вид системы линейных уравнений.
Справочный материал.
Общий вид системы линейных уравнений с неизвестными:
 (1)
(1)
В матричной форме система (1) имеет вид:
![]() ,
где
,
где
 ,
,
 ,
,
 (2)
(2)
Здесь
- матрица системы,
![]() - столбец неизвестных,
- столбец свободных членов.
- столбец неизвестных,
- столбец свободных членов.
Если определитель матрицы системы линейных уравнений с переменными
 ,
то единственное
решение системы определяется одним из
известных методов, например,
,
то единственное
решение системы определяется одним из
известных методов, например,
а. методом обратной матрицы по формуле:
![]() (3)
(3)
б. по формулам Крамера:
![]()
![]() ,
(4)
,
(4)
где
![]() - определитель матрицы, получаемой из
матрицы
заменой
-го
столбца столбцом свободных членов
.
- определитель матрицы, получаемой из
матрицы
заменой
-го
столбца столбцом свободных членов
.
Методом Гаусса можно решать любую систему уравнений вида (1).
С помощью элементарных преобразований над строками расширенная матрица системы (1) может быть приведена к виду:
 (5)
(5)
Матрица (5) является расширенной матрицей системы
 ,
(6)
,
(6)
которая с точностью до обозначения неизвестных эквивалентна исходной системе.
Если хотя бы одно
из чисел
![]() отлично от нуля, то система (6), а
следовательно и исходная система (1)
несовместны.
отлично от нуля, то система (6), а
следовательно и исходная система (1)
несовместны.
Если же
![]() ,
то система совместна и формулы (6) дают
по существу явное выражение для базисных
неизвестных
,
то система совместна и формулы (6) дают
по существу явное выражение для базисных
неизвестных
![]() через свободные неизвестные
через свободные неизвестные
![]() .
.
