3.3.3 Энергетические диаграммы р-n-перехода

Энергетические диаграммы р-n-перехода для прямого и обрат­ного напряжений показаны на рис. 3.7. Уровни Ферми в р- и n-областях в отличие от диаграммы для равновесного состояния (см. рис. 3.5) распо­лагаются на разной высоте, так что интервал между ними равен q|U|, т.е. пропорционален приложенному напряжению. Смещение границ зоны проводимости пропорционально высоте потенциального барь­ера и составляет и поясняет соотношение диффузион­ных и дрейфовых потоков носителей в переходе. [Рисунки 3.5 и 3.7 выполнены в разных масштабах.]

При прямом на­пряжении из-за сни­жения потенциаль­ного барьера нару­шается равенство диффузионного и дрейфового потоков как дырок, так и электронов: диффу­зионный поток ды­рок из р-области в n-область преобла­дает над встречным дрейфовым потоком дырок из n-области, а диффузия электронов из n-области в р-область – над встречным дрейфом электронов из р-области. В результате происходит увеличение концентрации не­основных носителей вне перехода в р- и n-областях. Этот процесс называется инжекцией неосновных носителей.

При обратном напряжении из-за увеличения потенциального барьера происходит ослабление диффузионных потоков по сравне­нию с состоянием равновесия. Уже при сравнительно небольшом обратном напряжении (порядка десятых долей вольта) диффузионный поток становится настолько малым, что дрейфовые потоки на­чинают преобладать над диффузионными. В результате дрейфа не­основных носителей происходит уменьшение концентраций неос­новных носителей у границ перехода: электронов в р-области и ды­рок в л-области. Это явление называется экстракцией (выведени­ем) неосновных носителей.

3.4. Вольт-амперная характеристика идеализированного р-n-перехода

Идеализированным является р-n-переход, для которого приня­ты следующие допущения.

1. В обедненном слое отсутствует генерация, рекомбинация и рассеяние носителей зарядов, т.е. предполагается, что ток носите­лей заряда одного знака одинаков на обеих границах перехода.

2. Электрическое поле вне обедненного слоя отсутствует, т.е. полупроводник вне перехода остается электрически нейтральным и в нем носители могут совершать только диффузионное движение.

3. Электрическое сопротивление нейтральных р- и n-областей считается пренебрежимо малым по сравнению с сопротивлением обедненного слоя, т.е. все внешнее напряжение практически полно­стью приложено к обедненному слою.

4. Границы обедненного слоя считаются плоскопараллельными, а носители заряда перемещаются по направлению, перпендикуляр­ному к этим плоскостям. Концентрации носителей зависят только от одной координаты.

Указанные предположения и используются для аналитического определения зависимости тока через переход от приложенного на­пряжения, называемой вольт-амперной характеристикой (ВАХ). Метод расчета «впитывает» в себя практически весь предыдущий материал (гл. 2 и гл. 3¹).

Для определенности изложения рассмотрим прямое напряжение (U > 0), когда происходит процесс инжекции неосновных носителей – появление избыточных концентраций неосновных носителей в каждой области, вызванное переходом основных носителей из противоположных областей.

По определению (2.30) прирост концентрации неосновных носителей в области n (дырок), т.е. избыточная концентрация их,

(3.23)

Аналогично избыточная концентрация электронов – неосновных носителей в p-области при инжекции

(3.24)

В этих выражениях и – равновесные значения концентраций при U=0, а и – неравновесные значения на границах обедненного слоя при подаче прямого напряжения U; при этом ,.

Для сохранения электрической нейтральности (см. § 2.2.1) должны появиться избыточные концентрации основных носителей на этих границах, чтобы выполнялось условие (2.31):

на границе с p-областью

(3.25)

на границе с n-областью

(3.26)

Т

(3.27)

(3.28)

еория р-n-перехода основана еще на одном важном предположении, что избыточные концентрации много меньше концентрации основных носителей:

Условия (3.27) и (3.28) означают, что концентрации основных носителей ипри подаче напряжения мало отличаются от равновесных значенийи, т.е. от­клонение от состояния равновесия невелико и можно считать, что связь концентра­ций электронов на границах обедненного слоя, а также связь концентраций дырок на этих границах определяется практически разностью потенциалов на этих граница () вместо_к в состоянии равновесия.

Связь для состояния равновесия может быть найдена из (3.9):

(3.29)

Для неравновесного состояния вместо (3.29) следует писать

(3.30)

Но так как, а, то получим

(3.31)

Из (3.31) получим зависимость избыточных концентраций неосновных носителей от U при инжекции:

(3.32)

Используя формулы (3.29) вместо (3.32) можно написать

,(3.33)

С учетом (3.33), (3.23) и (3.24) найдем избыточные концентрации неосновных но­сителей на границах перехода

,(3.34)

Зависимости (3.34) показаны на рис. 3.8. При U=0 = 0, =0 (состояние рав­новесия), при увеличении U (U>0) наблюдается экспоненциальный рост и .

Очевидно, что увеличение концентрации неосновных носителей при U > 0 на границах перехода приведет к их диффузии в глубь об­ластей: электронов – в р-области, дырок – в n-области. Диффузия будет сопровождаться рекомбинацией, поэтому концентрации из­быточных носителей будут убывать по направлению х (рис. 3.9), где х для обеих областей отсчитывается от границ перехода, чтобы мо­жно было применить формулы, аналогичные (2.62), (2.63):

,(3.35)

в которых и– значения избыточных концентраций носи­телей на границах перехода (х = 0), определяемые по формулам (3.34); L_n – диффузионная длина электронов в р-области; L_p – диф­фузионная длина дырок в n-области (при х = L_n и х = L_p избыточная концентрация электронов и избыточная концентрация дырок стано­вятся в е = 2,72 раза меньше, чем исоответственно.

Теперь остается сделать последний шаг: найти диффузионные токи, создаваемые избыточными электронами и дырками. Для этого следует использовать формулы (2.52). В этих формулах производ­ные надо определять для неравновесных концентраций ипо формулам (3.24) и (3.23):

и

Следовательно,

и

С учетом этого вместо формул (2.52) напишем

(3.36)

Подставив результаты дифференцирования (3.35) в формулы (3.36), получим значение плотности токов в любом сечении х:

(3.37)

Плотность диффузионного тока убывает по направлению (от границы перехода) и при х = 0 имеет максимальное значение

(3.37а)

Подставив в эти выражения ииз (3.34), получим

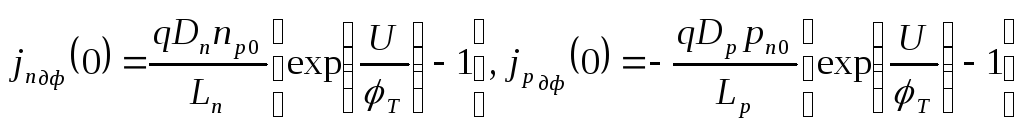(3.38)

Первое условие идеализации заключалось в том, что в отдель­ности электронный и дырочный токи по обе стороны перехода оди­наковы. Поэтому плотность полного тока в переходе можно опреде­лить как сумму плотности электронного тока на левой границе перехода и плотности дырочного тока на правой границе перехода. Тогда плотность полного тока с учетом (3.38)

По закону непрерывности тока найденная плотность будет в любом сечении n- и р-областей. Умножив на площадь сечения перехода S, получим формулу для тока:

(3.39)

Окончательно запишем эту формулу в виде

(3.40)

где

(3.41)

Выражение (3.40) и представляет собой вольт-амперную характери­стику идеализированного р-n-перехода (формула Шокли), а пара­метр называется тепловым током, так как его значение сильно зависит от температуры. Расчетные ВАХ приведены на рис. 3.10.

Поясним природу тока . По формулам (3.34) определялись из­быточные концентрации неосновных носителей на границах перехо­да (х = 0) при прямом напряжении и. При по­лучении этих формул не было ограничений на знак напряжения, поэ­тому они справедливы и для обратного напряжения. Однако для этого случая(U < 0) избыточные концентрации на границах перехо­да по формулам (3.34) становятся отрицательными. Зависимости их от обратного напряжения, соответствующие этим формулам, пока­заны на рис. 3.8 в третьем квадранте. Если модуль обратного напряжения |U| > 3_Т, то ,можно считать концент­рации избыточных неосновных носителей на границах перехода равными равновесным значениям, а полную концентрациюипрактически равной нулю.

При удалении от границ перехода избыточная концентрация убывает в соответствии с формулами (3.35). Вдали от перехода (х >> L_n, х >> L_p) полная концентрация равна равновесной (нет из­быточных неосновных носителей). Зависимость концентрации неосновных носителей от координаты при обратном напряжении по­казана на рис. 3.11.

Существование градиента концентрации неравновесных не­основных носителей означает появление на границах перехода диффузионных токов, плотность которых можно найти по форму­лам (3.37а), если положить в них , . При этом получим

Полученные токи протекают через переход в одном направлении. Складывая плотности токов и умножая на площадь сечения S, полу­чаем величину тока , представленную формулой (3.41).

Таким образом, ток , входящий в уравнение (3.40) ВАХ р-n-перехода, является диффузионным током неосновных носи­телей областей, переходящих при обратном напряжении в пере­ход. Однако в самом переходе они двигаются под действием уско­ряющего поля и создают дрейфовый ток. Диффузионный характер тока вне перехода и дрейфовый внутри него– такова осо­бенность природы тока .

Ток I в (3.40) содержит две составляющие с противоположным

знаком:

Первая составляющая зависит от напряжения, влияющего на высоту потенциального барьера, т.е. является диффузионной со­ставляющей тока (), вызванной теми основными носителями, которые смогли преодолеть барьер. Вторая составля­ющая (–) создается неосновными носителями обеих областей, для которых поле в обедненном слое является ускоряющим. Эта состав­ляющая является дрейфовой (I_др = –).

В состоянии равновесия (U = 0) диффузионная составляющая I_дф = и компенсируется встречным дрейфовым токомI_др = –, так чтоI = I_дф + I_др = 0. При прямом напряжении (U > 0) диффузионная составляющая превышает дрейфовую и ток I растет с увеличением U. Дрейфовой составляющей можно пренебречь при прямом на­пряжении U > 3_Т, т.е. для комнатной температуры при U = 0,075 В. При U>3_Т .

При обратном напряжении (U < 0) диффузионная составляю­щая из-за роста потенциального барьера убывает, так что начина­ет преобладать дрейфовая составляющая, остающаяся неизмен­ной. Диффузионной составляющей можно пренебречь перед дрейфовой при |U|/ _Т >3, т.е. для Т= 300 К U = – 0,075 В. В этом случае

Вольт-амперная характеристика для малых прямых напряже­ний (U<3_Т) и малых обратных напряжений (|U| < 3_Т) показана кривой 1 на рис. 3.10. Ветвь 1 ВАХ при U > 0 называется прямой ветвью, а ветвь 2 при U < 0 – обратной. При обратном напряжении, превышающем по модулю 3_Т , обратный ток не зависит от напря­жения и равен .

Рабочие прямые токи в р-n-переходах соответствуют напряже­ниям U>3_Т, при которых значение составляет 10³...10⁴. Поэтому приходится вводить различные масштабы для прямых и обратных токов (прямой и обратной ветвей ВАХ). В одном же масштабе (кри­вая 3) начальный участок прямой ветви ВАХ и обратная ветвь на рис. 3.10 не видны.

Тепловой ток (3.41) является важным параметром р-n-перехода. Его значение пропорционально равновесной концентрации не­основных носителей в нейтральных р- и n-областях.

Сильная зависимость от температуры, определившая его назва­ние, объясняется зависимостью от температуры концентрации неос­новных носителейи. С учетом формул (2.22) и (2.11)

Зависимость (T) характеризуют температурой удвоения T_удв – приращением температуры, приводящим к удвоению тока . Нетру­дно убедиться, что

(3.42)

При Т = 293К (t = 20°С) для кремния Т_удв = 5°С, для германия Т_удв = 8°С, для арсенида галлия Т_удв = 3,6°С. Нетрудно также определить изменение тока при любом приращении температуры : . Например, при изменении рабочей темпера­туры от –20 до 60°С отношение составит: для германия 2¹⁰ = 1024, для кремния 2¹⁶ = 6,55·10⁴ и для арсенида галлия 2²² = 410⁶.

Тепловой ток резко снижается с ростом ширины запрещенной зоны. При комнатной температуре _,Ge/,_Si ≈ 10⁶. Так как концентра­ция неосновных носителей обратно пропорциональна концентрации примеси, то также зависит от нее и тепловой ток: чем больше кон­центрация примесей, тем меньше .