Ответы на тестовые задания

Номер теста	3	4	5	6	7	8	9	10	11	12	13
Правильный ответ	2	3	3	1	2	1	1	3	1	1	1

Номер теста	14	15	16	17	18	19	20	21
Правильный ответ	3	2	2	2	1	2	1	1

Кривые второго порядка

Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных, называемых фокусами, есть величина постоянная, равная 2a, и большая чем расстояние между фокусами, равное 2c (рисунок 6).

Рисунок 6

Простейшее каноническое уравнение эллипса получается в системе координат, в которой за ось абсцисс выбрана прямая, соединяющая фокусы, начало координат 0 − середина отрезка, концами которого служат фокусы, ось ординат – прямая, проходящая перпендикулярно оси ОX через точку 0. Тогда уравнение эллипса примет следую- щий вид:

где

При таком выборе системы координат оси координат совпадают с осями симметрии эллипса, а начало координат − с центром симметрии. Точки А₁(a; 0), А₂(–a; 0), В₁(0; b), В₂(0; –b) называются вершинами эллипса. Отрезки, заключенные между вершинами, называются осями эллипса: большая (фокальная) ось А₁А₂ = 2a, малая ось В₁В₂ = 2b. Параметры a и b уравнения равны полуосям эллипса. Эксцентриситетом () эллипса называется отношение расстояния (2c) между фокусами к большей оси (2a), т. е. ; очевидно, что e < 1. Директрисами эллипса называются две прямые, параллельные малой оси и отстоящие от нее на расстоянии, равном . Уравнения директрис сле- дующие:

Пример 11. Составить каноническое уравнение эллипса, зная, что малая полуось равна 3 и эксцентриситет

Решение

Уравнение будем искать в виде

Из условия b = 3. Так как с одной стороны , а с другой стороны по условию то Откуда Для эллипса параметры a, b, c связаны соотношением Поэтому, подставляя значения b и c, получим уравнение

или

или

а² = 6.

Ответ:

Тест 22. Уравнение эллипса, полуоси которого равны a = 3, b = 2, имеет вид:

1)

2)

3)

Тест 23. Дано уравнение эллипса

Вычислить длину осей, фокусное расстояние, эксцентриситет:

1) 16; 9; 25;

2) 8; 6; 2

3) 4; 3; 1; 8.

Пример 12. Дан эллипс Написать уравнение его директрис.

Решение

Уравнения директрис следующие: . Из уравнения а² = 36, b² = 20. Следовательно, a = 6, или с = 4. Найдем e = Подставим в уравнения

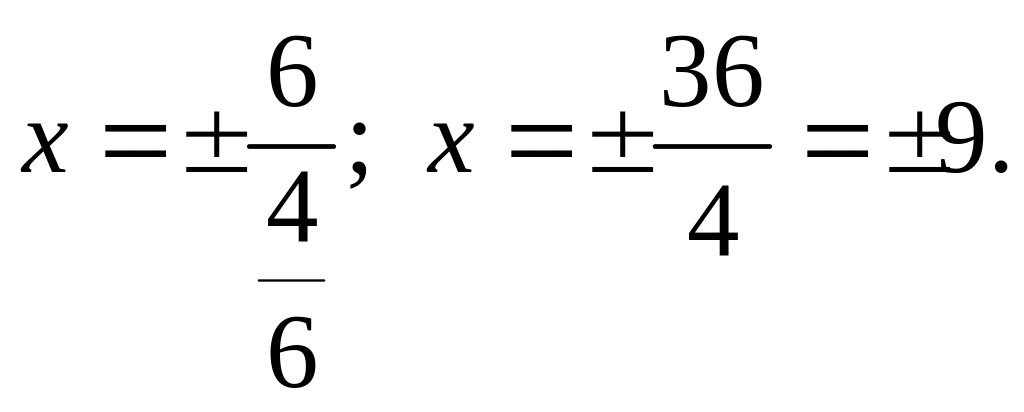
Ответ: x = 9.

Уравнение эллипса, центр которого находится в точке (х₀; у₀), а оси симметрии параллельны осям координат, имеет вид

Тест 24. Центр эллипса находится в точке:

1) (3; 1);

2) (3; –1);

3) (10; 5);

4) (5; 10).

Гиперболой называется множество точек плоскости, модуль разности от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2a, и меньшая чем расстояние между фокусами, равное 2c (рисунок 7).

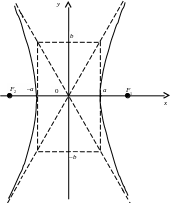
Рисунок 7

Простейшее каноническое уравнение гиперболы имеет вид

(1)

где b² = c² – a².

Прямая, соединяющая фокусы F₁, F₂ гиперболы, служит осью абсцисс, начало координат находится в середине между фокусами; при этом оси координат совпадают с осями симметрии гиперболы, начало координат – с ее центром симметрии (оси и центр гиперболы).

Гипербола имеет две действительные вершины А₁(a; 0), А₂(–a; 0) на фокальной оси; отрезок А₁А₂ = 2a называется действительной осью гиперболы, отрезок В₁В₂ = 2b – мнимой осью гиперболы. Таким образом, параметры a и b в уравнении гиперболы равны длинам действительной и мнимой полуосей соответственно.

Если a = b, то гипербола называется равносторонней.

Если мнимая ось гиперболы имеет длину 2a и направление по оси x, а действительная ось, длиной 2b, совпадает с осью y, то уравнение такой гиперболы имеет следующий вид:

(2)

где

Гиперболы (1) и (2) называются сопряженными гиперболами.

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к действительной оси: e = и при этом e > 1. Директрисами гиперболы называются прямые, перпендикулярные к фокальной оси и отстоящие на расстоянии, равном Уравнения директрис следующие: Асимптоты гиперболы определяются равенствами

Если точка, двигаясь по гиперболе, неограниченно удаляется, то расстояние ее от одной из асимптот стремится к нулю. Асимптоты являются диагоналями прямоугольника со сторонами 2a, 2b (рисунок 7).

Пример 13. Составить уравнение гиперболы, оси которой совпадают с осями координат, зная, что:

1. Расстояние между вершинами равно 8, а расстояние между фокусами – 10.

2. Действительная ось равна 6, гипербола проходит через точку (9; –4).

Решение

1. Уравнение гиперболы имеет вид

Так как расстояние между вершинами равно 8, то 2a = 8 или a = 4. Учитывая, что расстояние между фокусами равно 10, имеем 2c = 10, откуда c = 5. Найдем b² из соотношения b² = c² – а², т. е. b² = 5² – 4² = = 25 – 16 = 9.

Ответ:

2. Так как действительная ось равна 6, то 2a = 6 или a = 3. Поэтому уравнение гиперболы принимает вид Поскольку гипербола проходит через точку (9; –4), то ординаты этой точки обращают уравнение в истинное равенство, т. е. или или 9 – 1 = или b² = = 2.

Ответ:

Тест 25. Уравнение гиперболы, действительная ось которой равна 10 и лежит на оси ОX, а мнимая ось равна 16 и лежит на оси ОY, имеет вид:

1)

2)

3)

Тест 26. Дано уравнение гиперболы Вычислить длину осей, фокусное расстояние, эксцентриситет:

1) 10; 16; 2

2) 4; 5;

3) 5; 4;

Пример 14. Дана гипербола Написать уравнение ее директрис и асимптот.

Решение

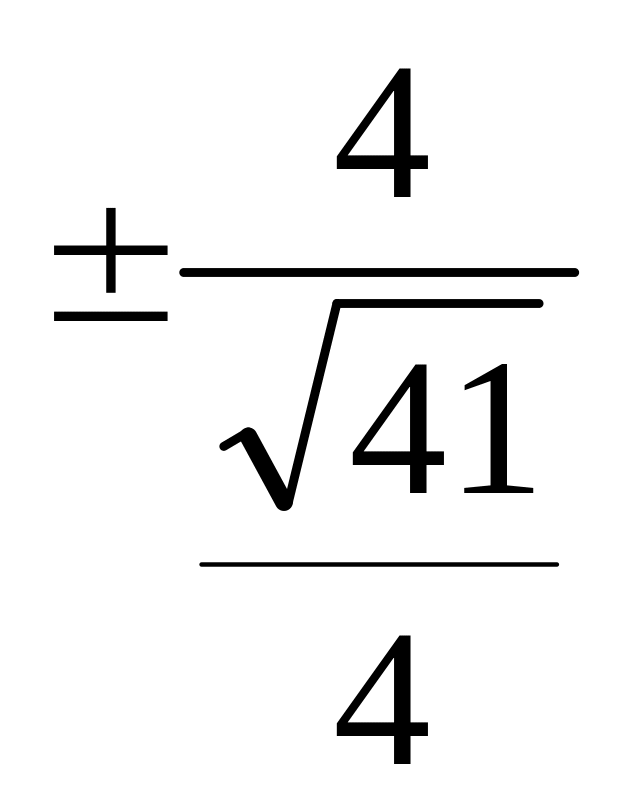Из уравнения а² = 16, b² = 25. Откуда a = 4, b = 5. Найдем Тогда уравнения директрис следующие: , или x = , или x =

Уравнения асимптот после подстановки a, b принимают вид y =

Ответ: x = y =

Тест 27. Указать, принадлежит ли точка (0; 2) гиперболе = 1:

1) да;

2) нет.

Уравнение гиперболы, центр которой находится в точке (х₀; у₀), действительная ось совпадает с осью ОX, мнимая – с осью ОY, имеет вид

Тест 28. Центр гиперболы находится в точке:

1) (5; 7);

2) (–5; –7);

3) (9; 16);

4) (3; 4).