Общая схема исследования функции и построения графика

Исследование функции y = f(x) целесообразно вести в определенной последовательности:

1. Найти область определения функции.

2. Исследовать функцию на четность, нечетность и периодичность.

3. Найти точки пересечения графика с осями координат.

4. Найти интервалы возрастания и убывания, экстремумы функции.

5. Найти интервалы выпуклости и вогнутости, точки перегиба.

6. Найти асимптоты.

7. Построить график функции.

Пример 6. Исследовать функцию и построить ее график.

Решение

Выполним все семь операций предложенной выше схемы исследования.

1. Функция не определена при x = 1 и x = –1. Область определения D(y) функции – вся числовая ось, за исключением точек x = 1 и x = –1, т. е.

2. Функция является нечетной, так как

Следовательно, график ее симметричен относительно начала коор- динат. Для построения графика достаточно исследовать ее при

3. Найдем точки пересечения графика с осями координат: с осью Oy график пересекается при х = 0, откуда y = 0, т. е. О(0; 0) – точка пересечения с осью Oy; с осью график пересекается, если у = 0, т. е. откуда х = 0.

Таким образом, О(0; 0) – единственная точка пересечения графика с осями координат.

4. Находим интервалы возрастания и убывания функции.

Находим первую производную

Можно увидеть, что y  0 в области определения, и функция является возрастающей на каждом интервале области определения.

Исследуем функцию на экстремум. Так как то критическими точками являются точки x₁ = 1 и x₂ = –1 (y не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.

5. Исследуем функцию на выпуклость. Находим y

Вторая производная равна нулю или не существует в точках х₁ = 0, На рисунке 38 представлена схема изменения знаков второй производной исследуемой функции.

Рисунок 38

Точка – точка перегиба графика функции.

График выпуклый вверх на интервалах (–1; 0) и (1; ); выпуклый вниз на интервалах (–; –1) и (0; 1).

6. Прямые x = 1 и x = –1 являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты

(k = 0 при x  + и при x  –),

Следовательно, есть горизонтальная асимптота, ее уравнение y = 0. Прямая y = 0 является асимптотой и при x  +, и при x  –.

7. График функции изображен на рисунке 39.

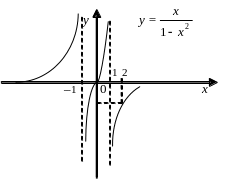
Рисунок 39

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7	8
Правильный ответ	1	4	3	3	2	4	1	5

2.7. Функции нескольких переменных Понятие функции нескольких переменных

Область определения

Переменная z называется функцией двух переменных x и y, если каждой паре (x; y) значений двух независимых друг от друга переменных величин x и y из некоторой области D соответствует определенное значение z: z = f(x; y).

Значение функции z = f(x; y) в точке M(x₀; y₀) обозначается z₀ = f(x₀; y₀) и называется частным значением функции.

Переменная величина и называется функцией трех переменных x, y, z, если каждому набору этих переменных соответствует единственное значение переменной u: u = f(x; y; z).

Будем пользоваться заданием функции, как правило, аналитическим способом: когда функция задается с помощью формулы.

Множество всех точек, в которых определена функция n переменных, называется областью определения функции.

Область определения находится из формулы функциональной зависимости путем соблюдения корректности выполнения соответ- ствующих математических операций.

В случае двух переменных область определения функции z = f(x; y) представляет собой некоторое множество точек на координатной плоскости Oxy, и тогда сама функция изображается в виде некоторой поверхности.

Пример 1. Найти f(1; 2) для функции