Ход работы и обработка результатов измерения

1. П

   № опыта	Длина маятника l, м	Квадратный корень из длины	Время десяти колебаний t,c	Период колебаний Т,с	g , м/c2
   1
   2

   одготовьте таблицу для записи измерений и вычислений.

2. Подвесьте маятник так, чтобы нить была по возможности более длинной.

3. Измерьте время десяти полных колебаний вашего маятника. Амплитуда колебаний должна быть по возможности малой. Вычислите период колебания по формуле (1).

4. Проведите те же измерения для маятников меньшей длины, каждый раз уменьшая длину на 5-10 см. (всего не менее 6 опытов с маятниками разной длины).

5. Полученные данные занесите в таблицу.

6. Постройте два графика: график зависимости периода колебаний от длины нити и график зависимости периода колебаний от квадратного корня из длины нити.

7. По полученным графикам сделайте выводы.

8. Рассчитайте величину ускорения свободного падения из формулы (2) для каждого опыта.

9. Вычислите среднее значение g_ср и рассчитайте погрешности.

10. Ответ представьте в виде g=(g_ср±Δg_ср)м/с² . Сравните полученный результат с табличным значением для ускорения свободного падения.

11. Сделайте вывод по работе.

Контрольные вопросы

1. Сделайте вывод уравнения гармонических незатухающих колебаний.

2. Как зависят от времени скорость и ускорение при гармонических незатухающих колебаниях? Чему равны максимальные значения скорости и ускорения?

3. Какие превращения энергии происходят при гармонических незатухающих колебаниях? Выведите закон сохранения энергии для гармонических незатухающих колебаниях.

4. От какнх величин зависит период математического маятника?

5. Зависит ли период колебаний математического маятника от амплитуды колебаний и массы груза?

6. Сформулируйте закон всемирного тяготения.

7. От каких величин зависит ускорение свободного падения?

ЛАБОРАТОРНАЯ РАБОТА № 7

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО

ТРЕНИЯ ЖИДКОСТИ ПО МЕТОДУ СТОКСА

Цель работы: Экспериментальное определение коэффициента внутреннего трения жидкости по методу Стокса.

Приборы и принадлежности: сосуд с жидкостью, шарики малого диаметра, микрометр, секундомер.

Вопросы к допуску

1. Какая физическая величина определяется в данной лабораторной работе?

2. Какие силы действуют на шарик, движущийся в жидкости?

3. Какие физические величины входят в рабочую формулу?

4. Можно ли начинать измерения от верхней границы жидкости?

5. Почему измерения нужно проводить, когда движение шарика станет равномерным?

К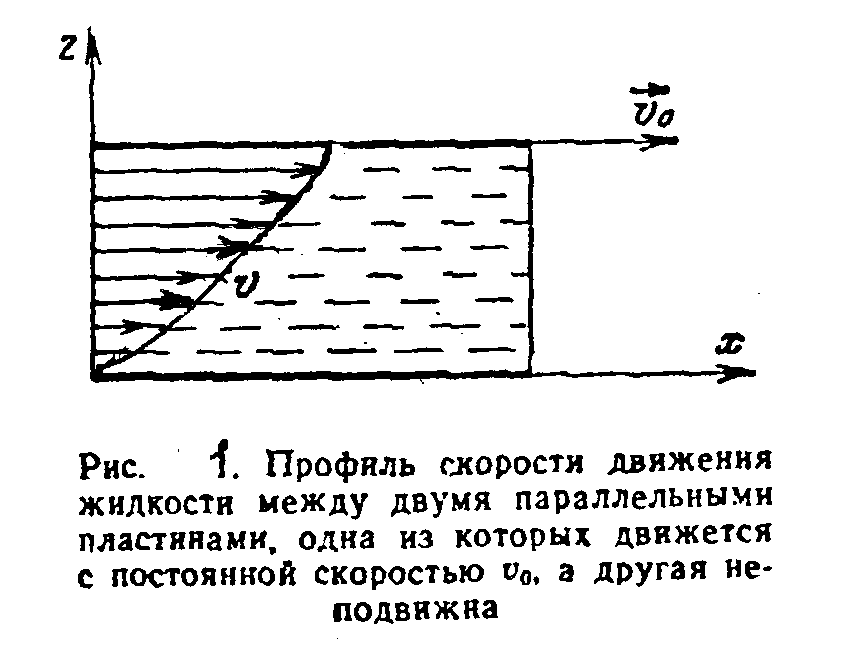 раткая теория

Внутреннее трение (вязкость) – свойство жидкостей и газов оказывать сопротивление при перемещении одной их части относительно другой. Рассмотрим схему вязкого ламинарного (слоистого) течения слоя жидкости, заключенного между двумя параллельными пластинами (рис.1). Пусть нижняя пластина неподвижна, верхняя движется горизонтально вправо со скоростью . Тогда в жидкости возникает течение со скоростью =(z).

Закон вязкого трения был установлен Ньютоном. Он имеет вид: , где F - касательная сила, вызывающая сдвиг слоев жидкости относительно друг друга; S - площадь слоя, по которому происходит сдвиг; - градиент скорости течения жидкости (быстрота изменения скорости от слоя к слою). В результате внутреннего трения происходит ускорение медленно движущихся и замедление быстро движущихся соседних слоев жидкости.

Коэффициент пропорциональности  - коэффициент внутреннего трения жидкости; иногда его называют вязкостью жидкости. В СИ размерность коэффициент внутреннего трения =Пас.

В условиях установившегося ламинарного течения при постоянной температуре Т коэффициент внутреннего трения жидкости  практически не зависит от градиента скорости.

Вязкость жидкостей (в отличие от вязкости газов) обусловлена в основном межмолекулярным взаимодействием, ограничивающем подвижность молекул. В настоящее время еще не существует адекватной теории вязкости жидкости, поэтому коэффициент внутреннего трения определяются экспериментально.

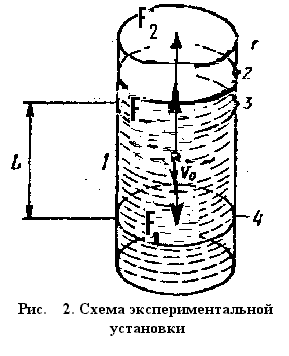
Одним из методов экспериментального определения коэффициента внутреннего трения вязких жидкостей является метод Стокса. При движении тела в жидкости на него действует сила сопротивления. Стокс вывел формулу для силы сопротивления, действующей на шар, движущийся в жидкости поступательно и с постоянной скоростью (вывод этой формулы требует знания специальных функций, поэтому мы его здесь не приводим). Формула Стокса имеет вид:

F=6r.

Здесь F-cила сопротивления жидкости при движении шара; -коэффициент внутреннего трения; r - радиус шара;  - скорость поступательного движения шара. Отметим, что формула Стокса справедлива лишь при условии, что при движении шара не возникает турбулентность (завихрение) жидкости. Движение прилегающих к шару слоев жидкости должно быть ламинарным (послойным). Это условие выполняется при

.

Здесь Re – число Рейнольдса – один из так называемых критериев подобия;  - плотность жидкости. Переход от ламинарного течения к турбулентному (вихревому) происходит в области значений 1000< Re<2000. При Re>2000, течение жидкости турбулентное.

Отметим, что критерии подобия дают возможность подбирать оптимальные условия эксперимента; они широко используются в гидродинамике, явлениях переноса, теории теплопередачи и др. Критерии подобия дают правила пересчета с модели на натурную конструкцию для явлений, в которых необходимо учитывать большое число факторов.