2 Формула Римана-Меллина .

Теорема 5 (формула Римана-Меллина). Пусть функция является оригиналом и имеет показатель роста , а – ее изображением. Тогда в любой точке , где оригинал непрерывен, справедлива формула Римана-Меллина

,

причем интегрирование производится вдоль любой прямой, интеграл понимается в смысле главного значения.

Без доказательства.

Определение 2. Формула Римана-Меллина

является обратной к формуле и называется обратным преобразованием Лапласа.

Теорема 6. Пусть – функция комплексного переменного , обладающая следующими свойствами:

1) функция , первоначально заданная в полуплоскости и удовлетворяющая в ней условиям:

а) – аналитическая функция в полуплоскости ,

б) в области 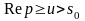функция стремится к нулю при равномерно относительно ;

в) для всех 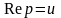, , 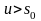сходится несобственный интеграл

,

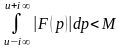где – некоторое положительное число, может быть аналитически продолжена на всю комплексную плоскость ;

2) аналитическое продолжение функции в полуплоскость 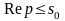удовлетворяет условиям леммы Жордана. Тогда имеет место следующее соотношение

,

где и – особые точки (полюсы, существенно особые точки) функции, являющейся аналитическим продолжением в полуплоскость , .

Без доказательства.

Пример. Найти оригинал функции .

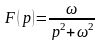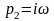Решение. Аналитическим продолжением функции в левую полуплоскость является функция , удовлетворяющая условиям леммы Жордана и имеющая две особые точки – полюсы первого порядка и . Поэтому при 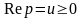и имеем

.

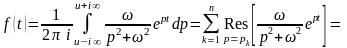
3 Операционный метод решения линейных дифференциальных уравнений и систем.

ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ К РЕШЕНИЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Постановка задачи: Требуется найти решение линейного дифференциального уравнения с постоянными коэффициентами

,

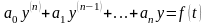удовлетворяющее начальным условиям Коши

, , , ,

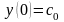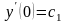где , , , – заданные числа, функция 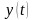вместе с ее рассматриваемыми производными и функция являются оригиналами.

Решение. Пусть , . Пользуясь свойствами дифференцирования оригинала и линейности, перейдем от оригиналов к изображениям:

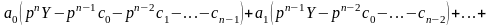
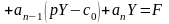
Разрешая это операторное уравнение относительно , получим:

.

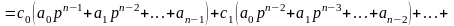
Положим

,

.

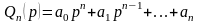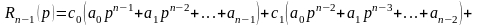
Тогда .

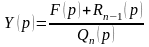Полученное решение называется операторным решением искомого дифференциального уравнения.

Определяя оригинал , соответствующий найденному изображению , получаем искомое решение.

Замечания. 1.Полученное решение во многих случаях оказывается справедливым при всех 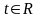, а не только при .

2. При нулевых начальных условиях решение операторного уравнения примет вид

.

Пример. Решить уравнение при начальных условиях , , .

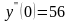Решение. Имеем . Тогда

,

,

.

Подставляя в дифференциальное уравнение и преобразовывая, получим

.

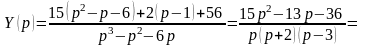
По таблице оригиналов находим

, , .

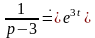Тогда получаем

.

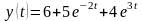ПРИМЕНЕНИЕ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ К РЕШЕНИЮ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Постановка задачи. Требуется найти решение системы линейных дифференциальных уравнений с постоянными коэффициентами

,

,

,

.

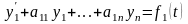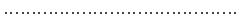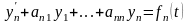удовлетворяющее начальным условиям Коши

, , , ,

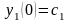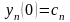где , , , – заданные числа, функции , , 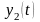, 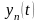вместе со своими первыми производными и функции , , , являются оригиналами.

Решение. Пусть 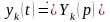, , . Применяя преобразование Лапласа к каждому уравнению системы и учитывая правила дифференцирования оригинала, получим

,

,

,

,

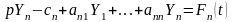или

,

,

,

.

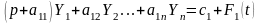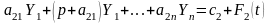Данная система называется системой операторных уравнений.

Пусть

есть определитель системы операторных уравнений и – алгебраические дополнения элементов, находящихся на пересечении -1 строки и -го столбца. Если определитель 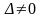, то применяя правило Крамера, получим

, .

Для нахождения решения исходной системы определяются оригиналы, соответствующие полученным изображениям.

Если определитель , то система операторных уравнений решения не имеет, следовательно, и исходная система не имеет решения.

Пример. Найти решение системы дифференциальных уравнений

,

,

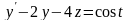удовлетворяющее начальным условиям 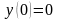и .

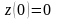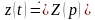Решение. Пусть и . Применяя преобразование Лапласа к данной системе, получим систему операторных уравнений

Определитель данной системы

.

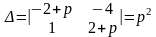Тогда решение относительно изображений есть

,

.

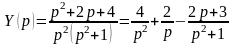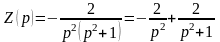Переходя от найденных изображений к оригиналам, получим при

,

.

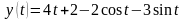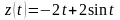При помощи операционного исчисления можно находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнениями в частных производных, уравнений в конечных разностях, проводить суммирование рядов. Вычислять интегралы. При этом решение этих и других задач значительно упрощается.