3. Свойства преобразования Лапласа.

Преобразование Лапласа обладает следующими свойствами.

1 (линейность). Линейной комбинации оригиналов соответствует линейная комбинация изображений, т.е. если и 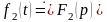и , – постоянные числа, то

.

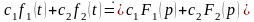► Находим изображение для функции :

. ◄

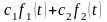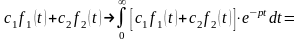
2 (подобие). Если и , то

.

► Находим изображение для функции

.◄

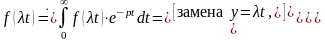
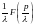3 (запаздывание). Если и , то .

► Находим изображение для функции

.◄

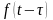
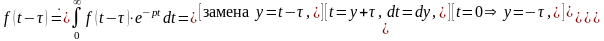
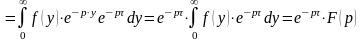Графики функций и имеют одинаковый вид, но график сдвинут на 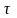единиц вправо. Это означает, что процесс, описываемый функцией , начинается с опозданием на время относительно процесса, описываемого функцией (рис.1).

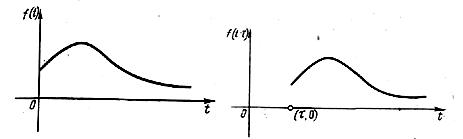
Рис.1.

4 (опережение). Если , то

.

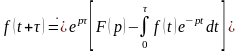► Находим изображение для функции

. ◄

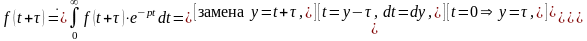
Графики функций и изображены на рисунке 2.

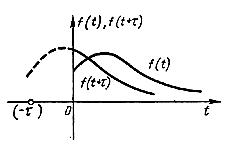
Рис.2.

5 (изображение периодической функции). Если оригинал имеет период 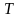, т.е. , то она может быть представлена в виде сходящегося ряда

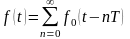, где

Тогда .

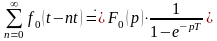► На основании теоремы запаздывания, имеем

,

,

,

,

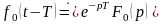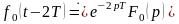где – изображение функции на начальном периоде.

Поэтому при достаточно больших ,

◄.

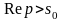
Пример. Найти изображение -периодичной функции

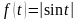
при , график которой представлен на рисунке 3.

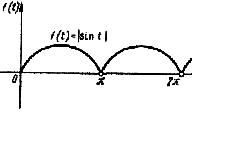
Рис.3.

Решение. Учитывая предыдущий пример, имеем

.

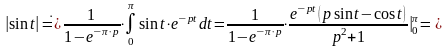
6 (затухание (смещение)). Если и – постоянное число, то

.

► Находим изображение для функции

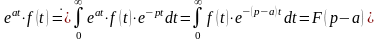
при .◄

7 (дифференцирование оригинала). Если и функции 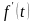, ,…, являются оригиналами, то

,

,

,

,

.

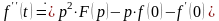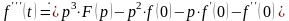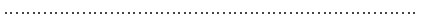► Находим изображение для функции

.

Находим изображение для функции , используя пункт 1:

.

Аналогично находятся изображения производных 3-го, 4-го и т.д. порядков.◄

8 (дифференцирование изображения). Если , то

,

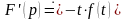,т

,

.

► Изображение согласно теореме 1 является аналитической функцией в полуплоскости . Следовательно, у нее существуют производные любого порядка. Функции являются оригиналами с показателями роста . Поэтому 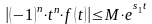, где .

Тогда получаем 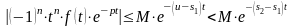, где , .

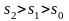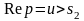Так как интеграл 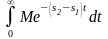существует, несобственный интеграл 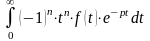равномерно сходится относительно в полуплоскости . Тогда возможно дифференцирование под знаком несобственных интегралов и

,

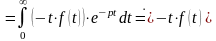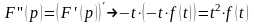и так далее. ◄

9 (изображение оригинала (интегрирование оригинала). Если , то

.

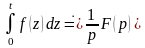► По свойству 4 оригиналов имеем, что функция является оригиналом с показателем роста и .

Так как , то 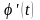также оригинал с показателем роста . Пусть . Используя свойство изображения производной оригинала, имеем . Так как , то .

Отсюда

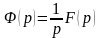
или , при .◄

Следствие. Пусть – непрерывный оригинал на интервале , и существует несобственный интеграл . Тогда имеет место соотношение .

10 (интегрирование изображения). Если и интеграл 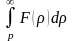сходится, то

.

► Имеем

.◄

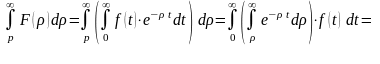
Следствие. Пусть

1) 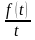– оригинал непрерывный на ,

2) ,

3) несобственный интеграл сходится.

Тогда имеет место равенство .
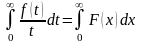