
- •Тема 16 элементы операционного исчисления
- •1 Определение преобразования Лапласа. Оригиналы и их изображения.
- •2 Существование изображения. Необходимый признак существования изображения. Единственность оригинала.
- •3. Свойства преобразования Лапласа.
- •Вопросы для самоконтроля
- •1 Теоремы разложения.
- •2 Формула Римана-Меллина .
- •3 Операционный метод решения линейных дифференциальных уравнений и систем.
- •4 Таблица оригиналов и их изображений
- •Вопросы для самоконтроля
- •Литература
Вопросы для самоконтроля
1. Дайте определение оригинала и перечислите их свойства.
2. Что называется изображением? Перечислите свойства изображений.
3. Дайте определение преобразования Лапласа. Перечислите свойства преобразования Лапласа.
Лекция 2. Обратное преобразование Лапласа.
1 Теоремы разложения.
2 Определение обратного преобразования Лапласа. Формула Римана-Меллина.
3 Операционный метод решения линейных дифференциальных уравнений и систем.
4 Таблица оригиналов и их изображений.
1 Теоремы разложения.
Теорема 1 (умножение
изображений).
Если
,
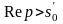 ,
и
,
,
и
,
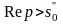 ,
то
,
то
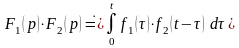 ,
,
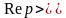
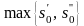 .
.
► Шаг 1.
Докажем, что функция
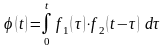 является оригиналом.
является оригиналом.
Условия 1) и 2)
очевидны. Возьмем
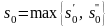 и
и
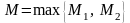 .
.
Тогда
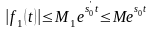 и
и
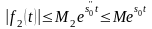 .
.
Следовательно,
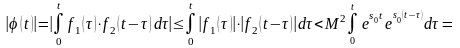
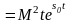 .
.
Так как при любом
малом
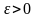 справедливо
справедливо
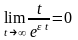 ,
то функция
,
то функция
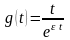 ограничена на интервале
,
т.е.
ограничена на интервале
,
т.е.
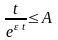 .
Отсюда
.
Отсюда
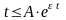 .
.
Тогда
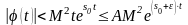 .
При
.
При
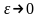 имеем, что функция
имеет ограниченный рост, показатель
которого равен
.
имеем, что функция
имеет ограниченный рост, показатель
которого равен
.
Шаг 2. Докажем формулу .
Используя преобразование Лапласа, можно записать
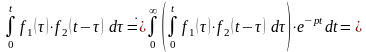
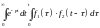 .
.
Область
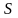 интегрирования данного двойного
интеграла определяется условиями
и
интегрирования данного двойного
интеграла определяется условиями
и
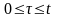 .
.
Изменяя порядок
интегрирования и полагая
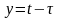 (рис.1),
(рис.1),
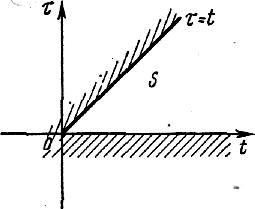
Рис.1.
получим
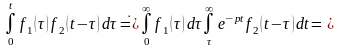
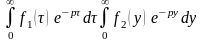
 .◄
.◄
Определение
1. Функция
вида
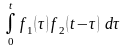 называется сверткой
функций
и
.
называется сверткой
функций
и
.
Обозначается:
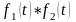 ,
т.е.
,
т.е.
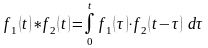 .
.
Положим . Тогда
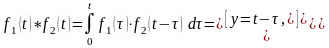
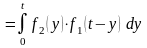 .
.
Видно, что свертка обладает свойством коммутативности.
Учитывая понятие свертки, теорему умножения можно записать в виде
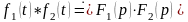 .
.
Следствие (формула
Дюамеля).
Пусть
и
– оригиналы,
,
,
и
,
,
причем
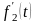 также является оригиналом. Тогда имеет
место равенство
также является оригиналом. Тогда имеет
место равенство
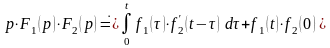 ,
,
где
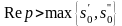 .
.
►Запишем произведение
 в виде
в виде
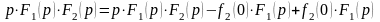 .
.
Отсюда
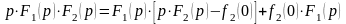 .
.
Первое слагаемое есть произведение изображений, соответствующих оригиналам и . Используя свойства умножения изображений и линейности, можно записать
 .
.
Тогда .◄
Пример.
Найти оригинал, соответствующий
изображению
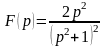 .
.
Решение. Поскольку
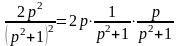 ,
,
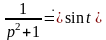 ,
,
 ,
,
то на основании формулы Дюамеля имеем
 .
.
Теорема 2 (1-я
теорема разложения).
Если функция
в окрестности точки
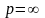 может быть представлена в виде ряда
Лорана
может быть представлена в виде ряда
Лорана
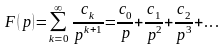 ,
,
то функция
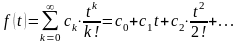 ,
,
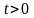 ,
является оригиналом, имеющим изображение
:
,
является оригиналом, имеющим изображение
:
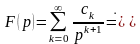
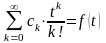 .
.
Без доказательства.
Пример.
Найти оригинал
,
если
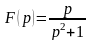 .
.
Решение. Запишем разложение в ряд Лорана функции данной в окрестности точки :
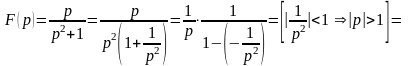
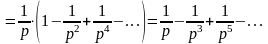 .
.
Следовательно,
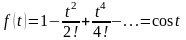 при
.
при
.
Теорема 3 (2-я
теорема разложения).
Если
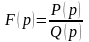 – рациональная правильная несократимая
дробь, знаменатель которой
– рациональная правильная несократимая
дробь, знаменатель которой
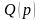 имеет лишь
простые корни
имеет лишь
простые корни
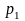 ,
,
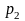 ,
,
,
,
 ,
то функция
,
то функция
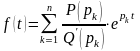
является оригиналом, имеющим изображение .
► Разложим
правильную рациональную дробь
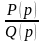 на простейшие:
на простейшие:
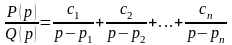 ,
,
где
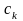 ,
,
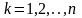 ,
– неопределенные коэффициенты.
,
– неопределенные коэффициенты.
Для определения
коэффициента
умножим обе части этого разложения на
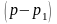 :
:
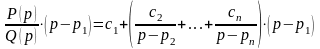 .
.
Переходя в этом
равенстве к пределу при
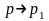 ,
получим
,
получим
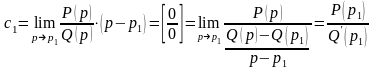 .
.
Аналогично находятся
коэффициенты
,
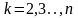 .
.
Подставляя найденные значения в разложение функции , имеем
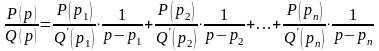 .
.
Известно, что
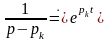 ,
.
На основании свойства линейности получим
,
.
На основании свойства линейности получим
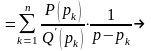
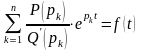 .
◄
.
◄
Замечания. 1.
Дробь
должна быть правильной. В противном
случае не выполняется необходимый
признак существования изображения
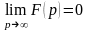 .
.
2. Видно, что коэффициенты , определяются как вычеты комплексной функции в простых полюсах
 .
.
Вторую теорему разложения можно сформулировать следующим образом.
Теорема 4 (3-я теорема разложения). Если – рациональная правильная несократимая дробь, , , , – простые или кратные полюсы знаменателя , то оригинал , соответствующий изображению , определяется формулой
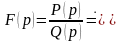
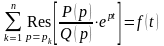 .
.
Без доказательства.
Пример.
Найти оригинал
функции
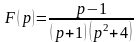 .
.
Решение.
Функция
правильная рациональная несократимая
дробь. Корни знаменателя
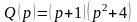 есть
есть
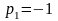 ,
,
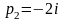 ,
,
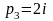 .
Применим 2-ю теорему разложения. Очевидно,
что
.
Применим 2-ю теорему разложения. Очевидно,
что
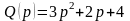 .
.
Тогда для имеем
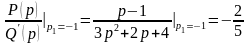 ,
,
для имеем
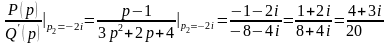 ,
,
для имеем
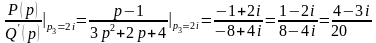 .
.
В итоге получим
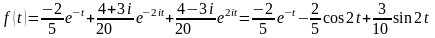 .
.
