Тема 16 элементы операционного исчисления
Лекция 1.Преобразование Лапласа
1 Определение преобразования Лапласа. Оригиналы и их изображения.
2 Существование изображения. Необходимый признак существования изображения. Единственность оригинала.
3 Свойства преобразования Лапласа.
1 Определение преобразования Лапласа. Оригиналы и их изображения.
Пусть
– комплекснозначная функция действительного
переменного
,
определенная на интервале
.
Определение 1. Любая комплекснозначная функция называется оригиналом, если она удовлетворяет условиям:
1)
при
;
2) при
функция
кусочно-непрерывна, т.е. на любом конечном
участке оси
имеет не более чем конечное число точек
разрыва первого рода;
3) при
функция
имеет ограниченную степень роста, т. е.
существует такое положительное постоянное
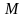и такое неотрицательное постоянное
,
что для всех
выполняется неравенство
,
,
.
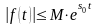Число
называется показателем
роста
функции
.
Свойства оригиналов
1. Если
— оригинал с показателем роста
,
то
является оригиналом с тем же показателем
роста.
2. Если
,
,
,
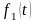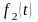– оригиналы с показателями роста
,
,
,
,
то функция
,
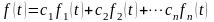где
,
,
,
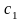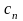– постоянные (действительные или
комплексные), является также оригиналом
с показателем роста
,
равным наибольшему из чисел
,
,
,
:
=
.
3. Если – оригинал с показателем роста , то являются оригиналами следующие функции:
– функция
,
,
имеющая показатель роста, равный
;
– функция
(
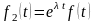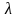— действительное или комплексное
число), показатель роста которой равен
– функция
,
,
имеющая показатель роста, равный
;
– функция
,
(
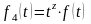— действительное или комплексное
число), показатель роста которой равен
.
4. Если
— оригинал с показателем роста
,
то функция
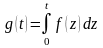на интервале
является непрерывным оригиналом с
показателем роста
.
Пример. Функция
называется единичной
функцией Хевисайда.
Функция
является оригиналом с показателем роста
.
Пусть функция
определена на интервале
;
и удовлетворяет условиям 2) и 3) определения
1, но
при
.
Тогда функция
является оригиналом.
Пример.
Найти показатель роста функции
,
где
– действительное или комплексное число.
Решение.
Если
,
то для функции
показатель ее роста
.
Если
,
то функция
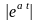является ограниченной и
.
Определение
2.
Изображением
(интегралом
Лапласа)
оригинала
называется несобственный интеграл
,
зависящий от комплексного параметра
.
Определение
3.
Преобразованием
Лапласа
называется операция перехода от оригинала
к изображению
.
Соответствие между
оригиналом
и изображением
записывается в виде
.
Пусть функция
является оригиналом с показателем роста
.
2 Существование изображения. Необходимый признак существования изображения. Единственность оригинала.
Теорема 1
(существование изображения).
Для любого
оригинала
изображение
существует в полуплоскости
,
где
– показатель роста функции
,
причем функция
является аналитической в этой
полуплоскости.
►Пусть
,
произвольная точка полуплоскости
.
Учитывая, что
,
,
,
имеем
.
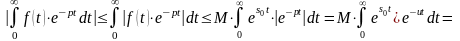
Таким образом,
.
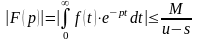Отсюда на основании признака сравнения сходимости несобственных интегралов следует абсолютная сходимость интеграла Лапласа. Значит, изображение существует и однозначно в полуплоскости .◄
Теорема 2
(необходимый признак существования
изображения).
Если функция
является изображением функции
,
то
.
► Справедливость
данной теоремы непосредственно вытекает
из неравенства
.◄
Теорема 3
(единственность оригинала).
Если функции
и
совпадают, то совпадают между собой и
соответствующие оригиналы
и
во всех точках, в которых они непрерывны.
Без доказательства.
Пример. Найти изображения функций
1) единичной функцией Хевисайда
2) , где – действительное или комплексное число.
Решение.
1. По формуле
при
находим
.
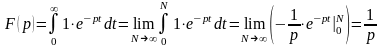Итак,
.
2. По формуле
при
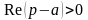имеем
.
Итак,
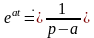при
.
Замечание.
Функция
является аналитической не только в
полуплоскости
,
но и на всей комплексной плоскости,
кроме точки
.
Такая особенность наблюдается и для
многих изображений.