Задачи для самостоятельной работы
1. Взятая на удачу деталь может оказаться либо первого ( событие А), либо второго ( событие В), либо третьего ( событие С) сорта. Что представляют собой следующие события:
?
Решение.
-
это событие, которое состоит при
наступлении хотя бы одного из событий
и
.
Следовательно,
в
нашем случае - деталь первого или
второго сорта.так как
- деталь первого или третьего сорта,
то противоположное этому событие
- деталь второго
сорта.
- невозможное
событие, поскольку деталь одновременно
не может быть и первого и второго сорта.
сумма невозможного
события и события
равно
, т.е.
- деталь третьего сорта.
2. В урне 5 красных, 2 синих и 3 белых шара. Все они пронумерованы цифрами 1,2,....10. Из урны берется наудачу 1 шар. Событие - шар с четным номером - обозначим через А, с номером, кратным 3, - через В, шар красного цвета - через С, синего - через D и, наконец белого через Е. Что представляют собой следующие события:
;
;
;
;
;
?
3.
Брошены 2 игральные кости. Найти
вероятность того, что сумма очков на
выпавших гранях равно 7. Ответ:
.
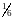4.
В коробке 6 одинаковых пронумерованных
кубиков. Из коробки наудачу по одному
извлекают все кубики без возвращения.
Найти вероятность того, что номера
извлекаемых кубиков появятся в
возрастающем порядке. Ответ:
.
5.
В коробке среди 40 лампочек 5 бракованных.
Студент покупает пять лампочек. Найти
вероятность того, что среди 5 купленных
лампочек 2 бракованные. Ответ:
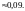
6.
В магазин поступило 30 новых цветных
телевизоров, среди которых 5 имеют
скрытые дефекты. Наудачу отбирается
один телевизор для проверки. Какова
вероятность, что он не имеет скрытых
дефектов? Ответ:
Определить вероятность события состоящего в том, что студенту придется ждать поезда
метров
10 секунд при условии, что интервал
движения поездов составляет 3 минуты.
Ответ:
8.
Набирая номер телефона абонент
забыл последние 3 цифры. Помня лишь то,
что эти цифры различны, абонент набрал
их наудачу. Найти вероятность того, что
набраны нужные цифры. Ответ:
.
Лекция №2 Свойства вероятностей. Условная вероятность. Теоремы сложения и умножения вероятностей.
Пусть
для некоторого случайного эксперимента
построено пространство элементарных
событий
Числовая неотрицательная функция
удовлетворяет следующим свойствам:
Если события
образуют полную группу событий, то
вероятность объединения этих событий
равна единице:
Вероятность противоположного события:
Если событие влечет за собой событие
,
то вероятность события
не превосходит вероятность события
,
т.е.
Пусть
и
-
наблюдаемые события в эксперименте ,
причем
.
Условной вероятностью
осуществления события
при
условии, что событие
произошло в результате данного
эксперимента, называется величина,
определяемая равенством:
Теорема сложения:
Пусть
событие
-совместные
события. Тогда вероятность их объединения
вычисляется по формуле:
.
Теорема умножения :
Вероятность
произведения событий
равна
произведению вероятностей событий,
причем вероятность каждого последующего
события вычисляется в предположении,
что все предыдущие имели место:
Формула полной вероятности. Формула Бейеса (теорема гипотез)
Пусть
случайный эксперимент можно описать
событиями
которые являются попарно несовместными
и
Такие события
называют гипотезами
. Предполагается,
что событие
может произойти с одной из гипотез
.
Теорема: Вероятность любого события , которое может произойти с одной из гипотез
будет равна сумме произведений вероятностей гипотез на условную
вероятность события :
-
формула полной вероятности.
Пусть
случайный эксперимент можно описать
попарно несовместными событиями
объединение которых образует пространство
элементарных событий
Событие
может произойти с одной из гипотез.
Предполагается, что в результате
эксперимента произошло событие
.
Как изменится вероятность гипотез при
этом? Ответ на поставленный вопрос дает
следующая теорема.
Теорема:
Пусть
событие
может произойти с одной из гипотез
Которые описывают случайный эксперимент. Если в результате реализации
эксперимента произошло событие , то вероятность гипотез вычисляются по
следующим формулам :
-
формулы Байеса.
Тесты для самоконтроля:
1.
Суммой двух событий
и
называют:
событие
,
состоящее из элементарных событий,
принадлежащих или событию
или
;событие
,
состоящее из элементарных событий,
принадлежащих или событию
или
;событие , состоящее из элементарных событий, принадлежащих и событию и ;
событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;событие
,
состоящее из элементарных событий,
принадлежащих и событию
и
;
2. Произведением двух событий и называют:
событие , состоящее из элементарных событий, принадлежащих или событию или ;
событие , состоящее из элементарных событий, принадлежащих или событию или ;
событие , состоящее из элементарных событий, принадлежащих и событию и ;
событие , состоящее из элементарных событий, принадлежащих и событию и ;
событие , состоящее из элементарных событий, принадлежащих и событию и ;
3.Вероятность
суммы двух совместных событий
равна:
Вероятность произведения двух совместных событий рана:
Формула полной вероятности:
Задачи для самостоятельной работы
В читальном зале имеется 6 учебников по теории вероятностей, из которых 3 в твердом переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника окажутся в твердом переплете.
Решение :
Пусть - первый взятый учебник имеет твердый переплет, - второй учебник имеет твердый переплет.
Вероятность того, что первый учебник имеет переплет
Вероятность того, что второй учебник имеет твердый переплет, при условии, что первый взятый учебник был в переплете, т.е. условная вероятность события
Искомая вероятность того, что оба учебника имеют переплет, по теореме умножения вероятностей зависимых событий равна
.
Найти вероятность того, что наудачу взятое двухзначное число окажется кратным 2,
либо 5, либо тому и другому одновременно. Ответ: 0,6.
В продукции часового завода брак составляет 5% от общего количества выпускаемых
часов.
Для контроля отобрано 20 часов. Какова
вероятность того, что среди них имеется
хотя бы одни часы с браком? Ответ :
В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3
человека.
Найти вероятность того, что все отобранные
лица окажутся мужчинами. Ответ:
В некоторую торговую точку поступает определенного вида товар от двух
производителей. Известно , что первый производитель поставляет 40% этого товара, а второй – 60%. Опыт показывает, что, как правило, 2% изделий первого производителя содержат брак а для второго производителя брак составляет 3%. Определить вероятность того, что случайно отобранное изделие содержит брак.
Решение
- событие, состоящее в том, что отобрано изделие, содержащие брак. Это событие может
произойти
с одним из событий
,
которое состоит в том, что изделие
поставлено
поставщиком.
Определим вероятности этих событий:
Условная вероятность будет равна:
Вычислим вероятность события , используя формулу полной вероятности.
Ответ: 0,026.
Находясь в условиях этой же задачи, предположим, что выбранное изделие содержит брак и определим вероятность того, что это изделие поставил первый поставщик. Воспользуемся формулами Байеса в виде:
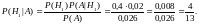
Ответ: 4/13.
Партия транзисторов, среди которых 10% дефектных, поступила на проверку. Схема
проверки такова, сто с вероятностью 0,95 обнаруживают дефект (если он есть), и существует ненулевая вероятность 0,03 того, что исправный транзистор будет признан дефектным. Какова вероятность того, что случайно выбранный из партии транзистор будет признан дефектным? Ответ: 0,122.
В продажу поступают телевизоры трех заводов. Продукция первого завода содержит
20% телевизоров со скрытым дефектом, второго –10%, третьего – 5%. Какова вероятность приобрести неисправный телевизор, если в магазин поступило 30% телевизоров с первого завода, 20% - со второго, 50% - с третьего? Ответ: 0,895