3.5. Линейные однородные ду n-го порядка

Полученные результаты можно распространить на линейные однородные дифференциальные уравнения n-го порядка, имеющие вид

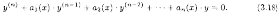
1. Если функции у₁=y₁(x),y₂=у₂(х),... ,у_n=у_n(х) являются частными решениями уравнения (3.18), то его решением является и функция У=c₁y₁+с₂у₂+...+с_nу_n.

2. Функции у₁, у₂,..., у_n называются линейно независимыми на (а;b), если равенство a₁y₁+а₂у₂+..+a_nу_n=0 выполняется лишь в случае, когда все числа а_i=0 (i=1,2, ...,n); в противном случае (если хотя бы одно из чисел из не равно нулю) функции у₁, у_2,..., у_n - линейно зависимы.

3. Определитель Вронского имеет вид

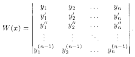
4. Частные решения y₁,y₂,...,y_n уравнения (3.18) образуют фундаментальную систему решений на (а;b), если ни в одной точке этого интервала вронскиан не обращается в нуль, т. е. W(x) ≠ 0 для всех х є (a; b).

5. Общее решение ЛОДУ (3.18) имеет вид у=c₁y₁+с₂у_{2 +...+}c_ny_n,

где c_i (i=1,... ,n) - произвольные постоянные, y_i- частные решения уравнения (3.18), образующие фундаментальную систему.

Пример 3.6. Показать, что функции образуют фундаментальную систему решений некоторого ЛОДУ третьего порядка (дополнительно: составить это уравнение).

Решение: Найдем W(x):

Ясно, что W(x)≠0 для всех х є R. Следовательно, данные функции образуют фундаментальную систему решений ЛОДУ третьего порядка. В общем виде ЛОДУ третьего порядка выглядит так:

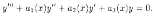
Подставив функции у₁,y₂,y₃ в это уравнение, получим систему из трех уравнений относительно функций а₁(х), а₂(х), а₃(х). Решая ее, получим ЛОДУ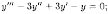 его общее решение:

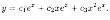
Лекция № 5

§4. Интегрирование ду второго порядка с постоянными коэффициентами

4.1. Интегрирование лоду второго порядка с постоянными коэффициентами

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.

Пусть дано ЛОДУ второго порядка

где р и q постоянны.

Для нахождения общего решения уравнения (4.1) достаточно найти два его частных решения, образующих фундаментальную систему (см. теорему 3.5).

Будем искать частные решения уравнения (4.1) в виде 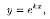где k - некоторое число (предложено Л. Эйлером).

Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение (4.1), получим:

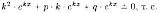
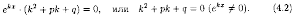
Уравнение (4.2) называется характеристическим уравнением ДУ (4.1)

(для его составления достаточно в уравнении (4.1) заменить у", у' и у соответственно на k², k и 1).

При решении характеристического уравнения (4.2) возможны следующие три случая.

Случай 1. Корни k₁ и k₂ уравнения (4.2) действительные и различные:

В этом случае частными решениями уравнения (4.1) являются функции y₁=e^k1^x и у₂=е^k2^x_. Они образуют фундаментальную систему решений (линейно независимы), т. к. их вронскиан

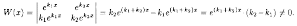
Следовательно, общее решение уравнения (4.1), согласно формуле (3.16), имеет вид

Пример 4.1. Решить уравнение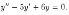

Решение: Составим характеристическое уравнение: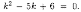 Решаем его: k₁=2, k₂=3. Записываем общее решение данного уравнения: 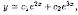где c₁ и с₂ - произвольные постоянные (формула (4.3)).

Случай 2. Корни k₁ и k₂ характеристического уравнения (4.2) действительные и равные:

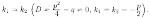
В этом случае имеем лишь одно частное решение y₁=e^k1x. Покажем, что наряду с у₁ решением уравнения (4.1) будет и у₂=хе^k1x. Действительно, подставим функцию у₂ в уравнение (4.1). Имеем:

Но k₁²+pk₁+q=0, т. к. k₁ есть корень уравнения (4.2); р+2k₁=0, т. к. по условию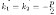

Поэтому y''₂+py'₂+qy₂=0, т. е. функция у₂=хе^k1^x является решением уравнения (4.1).

Частные решения 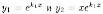образуют фундаментальную систему решений: W(x)=e^2k₁^x≠0. Следовательно, в этом случае общее решение ЛОДУ (4.1) имеет вид

Случай3. Корни k₁ и k₂ уравнения (4.2) комплексные: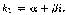

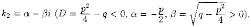
В этом случае частными решениями уравнения (4.1) являются функции

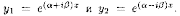
По формулам Эйлера

имеем

Найдем два действительных частных решения уравнения (4.1). Для этого составим две линейные комбинации решений y₁ и у_2:

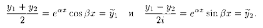
Функции 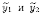являются решениями уравнения (4.1), что следует из свойств решений ЛОДУ второго порядка (см. теорему 3.2).

Эти решения 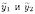образуют фундаментальную систему решений, так как W(x) ≠ 0 (убедитесь самостоятельно!). Поэтому общее решение уравнения (4.1) запишется в виде или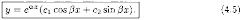

Пример 4.2. Решить уравнение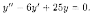

Решение: Имеем:

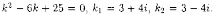По формуле (4.5) получаем общее решение уравнения:

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (4.1) сводится к нахождению корней характеристического уравнения (4.2) и использованию формул (4.3)-(4.5) общего решения уравнения (не прибегая к вычислению интегралов).