
- •Збірник вправ і задач з навчальної дисципліни “Основи початкового курсу математики”
- •Розділ 1. Математичні поняття, речення і доведення
- •1.1. Математичні поняття. Обсяг і зміст поняття. Означення понять, вимоги до означення понять
- •1.2. Висловлення, висловлюванні форми
- •1.3. Відношення слідування і рівносильності математичних речень. Необхідні і достатні умови
- •1.4. Структура теореми. Види теорем
- •1.5. Способи розв’язування текстових задач
- •Розділ 2. Множини і операції над ними
- •2.1. Поняття множини, способи задання множин. Відношення між множинами
- •2.2. Перетин та об’єднання множин, доповнення підмножини
- •2.3. Декартовий добуток множин
- •2.4. Зображення декартового добутку двох числових множин
- •2.5. Комбінаторні задачі
- •Розділ 3. Відповідності і відношення
- •3.1. Поняття бінарного відношення між елементами однієї множини. Способи задання бінарних відношень
- •3.2. Відношення еквівалентності
- •3.3. Відношення порядку
- •3.4. Поняття відповідності
- •3.5. Взаємно однозначні відповідності
- •Розділ 4. Поняття числа і дій над натуральними числами
- •4.1. Поняття натурального числа і числа нуль
- •4.2. Теоретико-множинний зміст суми і різниці натуральних чисел
- •4.3. Теоретико-множинний зміст добутку цілих невід’ємних чисел
- •4.4. Відношення «більше в», «менше в»
- •4.5. Ділення з остачею
- •Розділ 5. Запис чисел і алгоритм дій над ними
- •5.1. Додавання багатоцифрових чисел
- •5.2. Віднімання багатоцифрових чисел
- •5.3. Множення багатоцифрових чисел
- •5.4. Ділення багатоцифрових чисел
- •Розділ 6. Подільність цілих невід’ємних чисел
- •6.1. Поняття відношення подільності, його властивості
- •6.2. Подільність суми, різниці і добутку цілих невід’ємних чисел
- •6.3. Найбільший спільний дільник і найменше спільне кратне
- •6.4. Ознаки подільності чисел на 2, 3, 4, 5, 9
- •6.5. Алгоритм Евкліда
- •Розділ 7. Додатні раціональні числа
- •7.1. Поняття дробу. Поняття додатного раціонального числа
- •7.2. Запис додатних раціональних чисел у вигляді десяткових дробів
- •7.3. Додавання і віднімання раціональних чисел
- •7.4. Множення і ділення додатних раціональних чисел
- •7.5. Нескінченні десяткові періодичні дроби
- •Розділ 8. Дійсні числа
- •8.1. Поняття додатного дійсного числа
- •8.2. Дії над дійсними числами
- •8.3. Від’ємні числа
- •Розділ 9. Рівняння, нерівності, функції
- •9.1. Поняття про рівняння. Рівносильність рівнянь з однією змінною
- •9.2. Поняття нерівності. Рівносильність нерівностей
- •9.3. Поняття про функцію
- •9.4. Лінійна функція
- •9.5. Пряма і обернена пропорційності
- •Розділ 10. Поняття величини, її вимірювання
- •10.1. Поняття величини та поняття вимірювання величин
- •10.2. Довжина відрізка і його вимірювання
- •10.3. Площа фігури і її вимірювання
- •10.4. Проміжки часу і їх вимірювання
- •Література
7.3. Додавання і віднімання раціональних чисел
1. Додайте дроби, попередньо скоротивши їх, якщо це можливо:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() .
.
2. Обчисліть найбільш раціональним способом, використовуючи закони додавання:
1)
![]() ; 2)
; 2)
![]() ;
;
2)
![]() .
.
3.
Знайдіть різницю: 1)
![]() ;
2)
;
2)
![]() .
.
4.
Суму чисел
![]() і
і
![]() зменште на
зменште на
![]() .
Скількома способами можна це зробити?
.
Скількома способами можна це зробити?
5.
Яке з чисел ближче до 1:
![]() чи
чи![]() ?
?
6. Знайдіть значення виразу:
1)
 ;
;
2)
 .
.
7.4. Множення і ділення додатних раціональних чисел
1. Запишіть, використовуючи символи, закони множення додатних раціональних чисел і доведіть їх.
2. Обчисліть, використовуючи закони множення:
1)
![]() ; 3)
; 3)
![]() ;
;
2)
![]() ; 4)
; 4)
 .
.
3. Виконайте вказані дії:
1)
![]() ; 2)
; 2)
 ; 3)
; 3)
 .
.
4.
Розв’яжіть рівняння, використовуючи
залежність між компонентами і результатами
дій: 1)
 ;
2)
;
2)
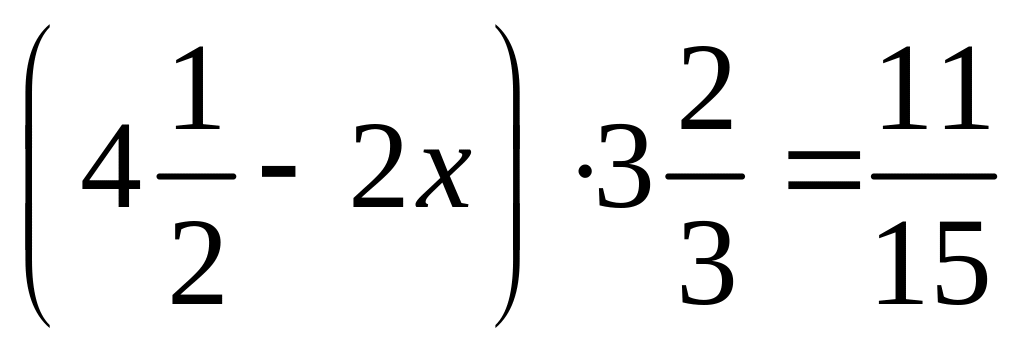 ;
3)
;
3)
 ;
4)
;
4)
 .
.
5. Розв’яжіть арифметичним способом задачі:
1) Дівчинка прочитала
324 сторінки книжки за чотири дні. За
перший день вона прочитала
![]() всієї книжки, за другий і третій дні –
по
всієї книжки, за другий і третій дні –
по
![]() того, що залишилося після першого дня.
Скільки сторінок прочитала дівчинка
за четвертий день?
того, що залишилося після першого дня.
Скільки сторінок прочитала дівчинка
за четвертий день?
2) У квартирі дві
кімнати. Довжина однієї дорівнює
![]() м, довжина іншої складає
цієї довжини. Ширина кожної кімнати
м, довжина іншої складає
цієї довжини. Ширина кожної кімнати
![]() м. Площа цих кімнат складає
м. Площа цих кімнат складає
![]() площі всієї квартири. Чому дорівнює
площа квартири?
площі всієї квартири. Чому дорівнює
площа квартири?
3) Група туристів
запланувала пройти шлях від турбази до
озера за чотири дні. За перший день вони
планували пройти
![]() всього шляху, за другий
,
що залишився, а за третій і четвертий
проходити по 12 км. Яка довжина всього
шляху від турбази до озера?
всього шляху, за другий
,
що залишився, а за третій і четвертий
проходити по 12 км. Яка довжина всього
шляху від турбази до озера?
6. Дані задачі розв’яжіть різними способами:
1) Шлях від міста А до міста В складається з двох рівних за довжиною ділянок. На першій ділянці автобус йшов зі швидкістю 55 км/год, а на другій – зі швидкістю 65 км/год, витративши на весь шлях 6 годин. Скільки часу витратив автобус на проходження кожної ділянки шляху?
2) Весь шлях між містами А і В вантажний автомобіль проходить за 4 години 15 хвилин при середній швидкості 48 км/год. За який час пройде цей шлях легковий автомобіль, якщо його середня швидкість 84 км/год?
7.5. Нескінченні десяткові періодичні дроби
1.
Поясніть, чому дроби
![]() і
і
![]() не можна записати у вигляді скінченного
десяткового дробу.
не можна записати у вигляді скінченного
десяткового дробу.
2.
Подайте число
![]() у вигляді нескінченного десяткового
дробу та поясніть, чому цей дріб є
періодичним.
у вигляді нескінченного десяткового
дробу та поясніть, чому цей дріб є
періодичним.
3.
Запишіть у вигляді нескінчених десяткових
дробів наступні звичайні дроби: 1)
;
2)
![]() ;
3)
;
3)
![]() .
.
4. Запишіть у вигляді звичайного дробу:
1) 0,(43); 2) 0,(301);
3) 5,7(27); 4) 6,31(8);
5) 15,43(29).
5. Доведіть, що 0,27(9) = 0,28(0).
6. Встановіть, які з наступних рівностей істинні:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
7. Розташуйте числа у порядку зростання:
1) 0,125; 2,(7); 0,1(25);2,78; 2) 1,(5); 0,(12); 2,778; 2,(778).
Розділ 8. Дійсні числа
8.1. Поняття додатного дійсного числа
1. Опишіть процес десяткового вимірювання довжини відрізка, якщо звіт про нього представляється у вигляді: 1) 3,46; 2) 3,(7); 3) 3,12311223… .
2. Доведіть, що не існує додатного раціонального числа, квадрат якого дорівнює 3.
3. Чи є трикутник ABC, зображений на рисунку 21, рівностороннім?

Рис. 21.
4. Сьома частина одиниці довжини вміщується у відрізок AB 13 разів. Скінченним чи нескінченим дробом виражається довжина цього відрізка? Періодичним чи неперіодичним?
5. Доведіть, що сума раціонального числа q і ірраціонального числа α завжди буде число ірраціональне.
Вказівка. Доведення ведіть від супротивного.
6.
Порівняйте значення виразів: 1)
![]() і
і
![]() ;
2)
;
2)
![]() і
і
![]() .
.
7.
Спростіть вирази 1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
