Эпюр №3 по теме «Пересечение поверхностей»

3.1 Содержание эпюра:

Требуется:

задача 1 – построить линию пересечения поверхности вращения проецирующей плоскостью;

задача 2 – построить линию пересечения поверхности вращения и многогранника;

задача 3 – построить линию пересечения двух поверхностей вращения способом секущих плоскостей;

задача 4 – построить линию пересечения двух поверхностей вращения способом вспомогательных секущих сфер.

Рекомендации по выполнению эпюра:

3. Чертеж должен быть выполнен в соответствии с ГОСТми: 2.301 – 68^* (Форматы), 2.302 - 68^* (Масштабы), 2.303 - 68^* (Линии), 2.304 – 81 (Шрифты) (приложение 4);

4. После выполнения чертежа выполнить его обводку (возможно оформление в цвете, но цвет и тональность должны быть такими, чтобы были читаемы линии построения).

Указания к выполнению эпюра:

1. Студенты факультета МСХ выполняют задачи 1 – 4 на 4 – 5 листах формата А3 (рисунки 3.3 – 3.7). Студенты факультета ПГС выполняют задачи 1 – 4 не выполняя аксонометрической проекции в первой задаче на 4 – 5 листах формата А3 (рисунок 3.3, 3.4, 3.6, 3.7).

2. Данные для выполнения эпюра взять из приложения 1 в соответствии с вариантом. Размеры даны в миллиметрах. Задачи эпюра выполняются на листах ватмана формата А3, в масштабе 1:1 или 2:1, в зависимости от исходных размеров. Основная надпись выбирается в соответствии с факультетом из приложения 3. Размеры наносить не ненужно, так как в противном случае они будут накладываться на линии построения.

3.2 Порядок выполнения эпюр

Задача 1 - Пересечение поверхности вращения проецирующей плоскостью.

Последовательность выполнения задания:

1. Построить проекции сечения геометрического тела проецирующей плоскостью;

2. Определить натуральную величину сечения;

3. Выполнить аксонометрическое изображение усеченной части геометрического тела;

4. Построить полную развертку поверхности усеченной части геометрического тела.

Порядок построения:

1. Строим проекции линии пересечения конуса проецирующей плоскостью Р. Искомую линию можно построить двумя способами.

1 способ (рисунок 3.3)

Точки 1₂ и 7₂, принадлежащие контурным образующим конуса, переносим по линии связи на горизонтальную проекцию конуса, получаем точки 1₁ и 7₁ . Горизонтальную проекцию основания делим циркулем на 12 частей и через полученные точки и вершину конуса проводим его образующие, а затем строим их фронтальные проекции. Находим точки 2₂', 2₂, 3₂', 3₂, 5₂', 5₂, 6₂', 6₂ как пересечения образующих с фронтальным следом плоскости Р₂ и находим их горизонтальные проекции проецируя на соответствующие образующие в плоскости П₁. Для построения точек 4₁', 4₁ проведем дополнительную секущую плоскость Т, фронтальный след которой проходит через точки 4₂', 4₂ и параллелен проекции основания конуса. Фигурой сечения конуса плоскостью Т будет окружность, радиус которой равен расстоянию от оси конуса до его контурной образующей, измеренный по следу плоскости Т. Построив горизонтальную проекцию окружности, находим на ней проекции точек 4₁', 4₁. Профильную проекцию линии пересечения строим по ее фронтальной и горизонтальной проекции.

Соединив последовательно найденные точки в плоскости П₁, получим горизонтальную проекцию линии пересечения конуса данной плоскостью Р. Построенная линия будет видимой, так как в горизонтальной плоскости проекции боковая поверхность конуса является полностью видимой. В плоскости П₃ так же точки соединяются последовательно, но предварительно определив видимость. В профильной плоскости проекции видима будет та часть конуса, которая в плоскости П₂ находится слева от оси конуса. Значит точки 1₃, 2₃', 2₃, 3₃', 3₃ будут видимыми в плоскости П₃, а 5₃', 5₃, 6₃', 6₃ – не видимы, точки 4₃', 4₃ являются пограничными.

2 способ (рисунок 3.4)

Точки 1₂, 6₂, принадлежат контурным образующим конуса, и перенесем их по линиям связи на горизонтальную проекцию конуса. Точки 1₁, 6₁ находятся на оси. Для нахождения дополнительных точек введем дополнительные секущие горизонтальные плоскости уровня (H, T, R, Q).

Фронтальные проекции точек 2₂', 2₂ находятся на пересечении следа данной плоскости Р₂ и следа введенной плоскости Q₂. Для построения горизонтальных проекций 2₁', 2₁, построим в плоскости П₁ фигуру сечения конуса плоскостью Q. Искомая фигура будет окружностью, радиус которой равен расстоянию от оси конуса до его контурной образующей, измеренный по следу плоскости Q₂. построив окружность, находим на ней с помощью линии связи проекции точек 2₁', 2₁. Точки 2₃', 2₃ находятся по двум уже построенным проекциям. Остальные точки 3', 3, 4', 4, 5', 5 строятся аналогично. Видимость линии пересечения определяется точно так же как в первом способе решения задачи.

2. Для определения натуральной величины (н.в.) сечения применен метод замены плоскостей проекций. Дополнительная плоскость мысленно проводится перпендикулярно плоскости проекций П2 и параллельно следу Р₂. Из каждой точки фронтальной проекции фигуры сечения проводим перпендикуляры к полученной оси сечения (рисунок 3.3). Точки 1 и 7 будут находиться на оси, положение остальных точек определяем, используя заменяемую плоскость П1. Например, на перпендикуляре, проходящем через точки 2 и 2' отложим расстояние [2₁2'₁], измеренное на горизонтальной проекции фигуры сечения. Таким же образом определяется положение остальных точек. Соединив их между собой, получим натуральную величину сечения.

3. Для выполнения аксонометрического изображения усеченного конуса используем прямоугольную изометрическую проекцию (оси х, у, z расположены под углом 120˚ относительно друг друга).

Строим аксонометрическое изображение основания конуса (эллипс). Построения приведены на рисунке 3.1. Радиус основания конуса замеряем с горизонтальной плоскости проекции.

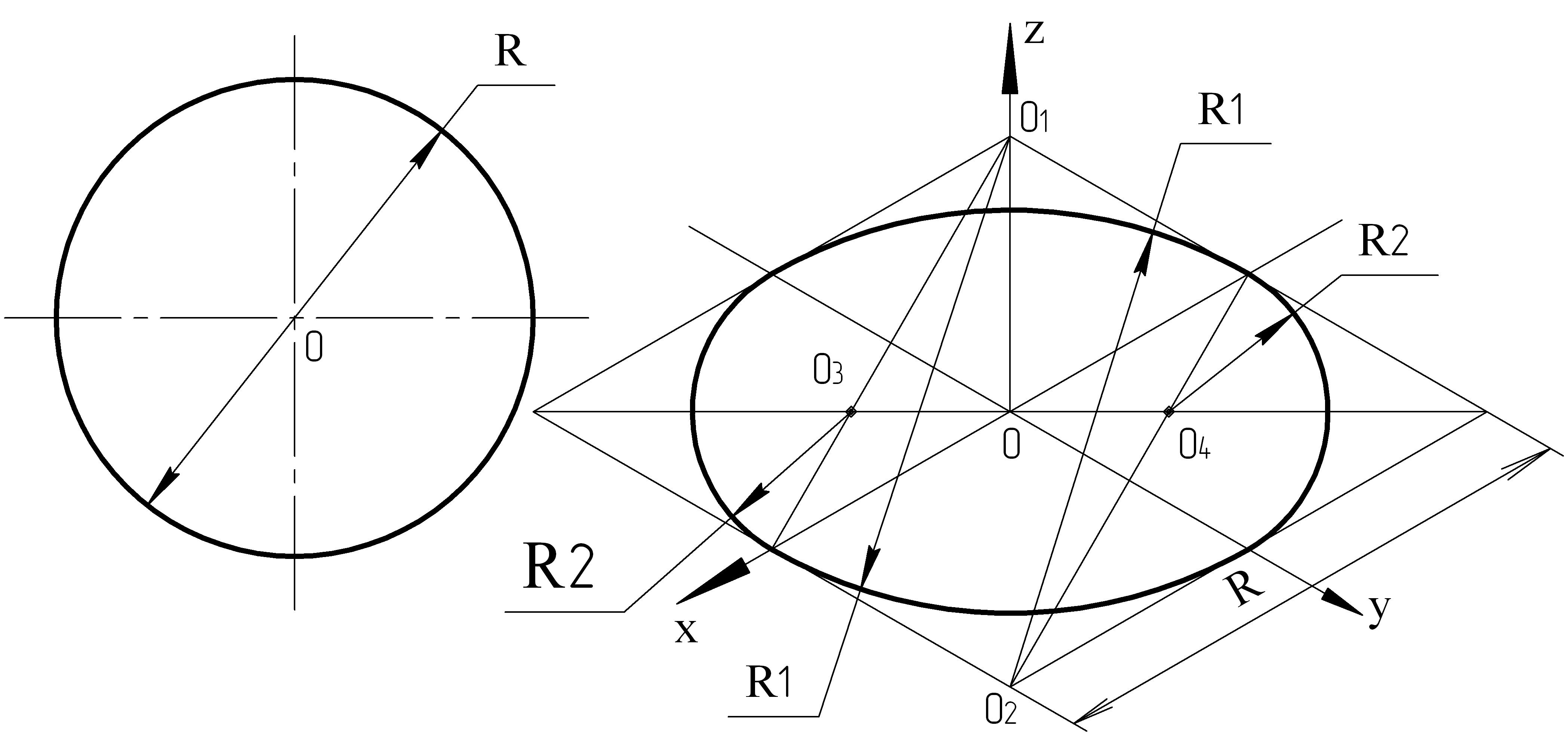
Рисунок 3.1 – Построение прямоугольной изометрической проекции окружности.

Следующим шагом является построение фигуры сечения конуса, ограниченной линией построенной на первом этапе решения задачи (см. рисунок 3.3). Для этого необходимо построить аксонометрические проекции точек 1, 2, 2', 3, 3', 4, 4', 5, 5', 6, 6', 7.

Для нахождения, например, точки 1 нужно замерить расстояние от точки О₁ до точки 1₁ и отложить его на оси х. Из полученной точки провести прямую параллельную оси z и отложить на ней высоту от основания конуса до точки 1₂, замеряемую с плоскости П₂. Получаем точку 1. Остальные точки строятся аналогично (рисунки 3.3 и 3.5)

4. Развертку конуса можно построить несколькими способами (подробное описание построения разверток геометрических тел находится в приложении 2).

Рассмотрим построение развертки конуса для решения, предложенного на рисунке 3.3.

Из произвольно выбранной точки проводим прямую и откладываем на ней расстояние равное длине боковой образующей, которую замеряем на плоскости П₂. Затем из выбранной точки проводим дугу радиусом, равным длине контурной образующей. На этой дуге циркулем откладываем 12 равных хорд, длину которых замеряем на горизонтальной плоскости проекции. Проводим образующие через вершину конуса и точки деления, получаем развертку боковой поверхности конуса.

На полученных образующих откладываем от основания конуса расстояния, необходимые для построения кривой линии на развертке боковой поверхности. Расстояния замеряем с фронтальной проекции, предварительно определив натуральную величину. Для этого используют метод вращения. Принцип построения показан на рисунке 3.2.

Отрезок [А1] - расстояние от основания конуса до точки сечения; [А₁1₁] и [А212] - его горизонтальная и фронтальная проекции. Вращаем отрезок [А111] вокруг оси конуса до положения, параллельного фронтальной плоскости, т.е переносим его на горизонтальную ось основания конуса, а затем находим проекции точек А₂' и 1₂' на контурной образующей конуса. Полученный отрезок [А2'12'] - натуральная величина расстояния [А-1]

Соединив полученные точки 1, 2, 3, 4, 5, 6, 7, 2', 3', 4', 5', 6', 7 строим развертку боковой поверхности конуса. На продолжении образующей, проходящей через точку 7, строим натуральную величину сечения и основание конуса (рисунок 3.3)

Рисунок 3.2 – Нахождение натуральной величины части образующей конуса методом вращения.

Задача 2 - Пересечение многогранника и поверхности вращения

Последовательность выполнения задания:

1. Построить линию пересечения многогранной поверхности и поверхности вращения;

2. Построить полную развертку многогранника и нанести на ней линию пересечения поверхностей.

Линия пересечения двух поверхностей строится способом вспомогательных секущих плоскостей (уровня или проецирующих). С их помощью определяют характерные точки и промежуточные точки линии пересечения. Плоскость следует выбирать так, чтобы линии ее пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые). Когда боковая поверхность цилиндра или призмы занимает относительно плоскости проекций проецирующее положение (образующие поверхности перпендикулярны этой плоскости проекций), то одна проекция линии пересечения становится известной без дополнительных построений, она совпадает с проекцией поверхности.

Порядок построения:

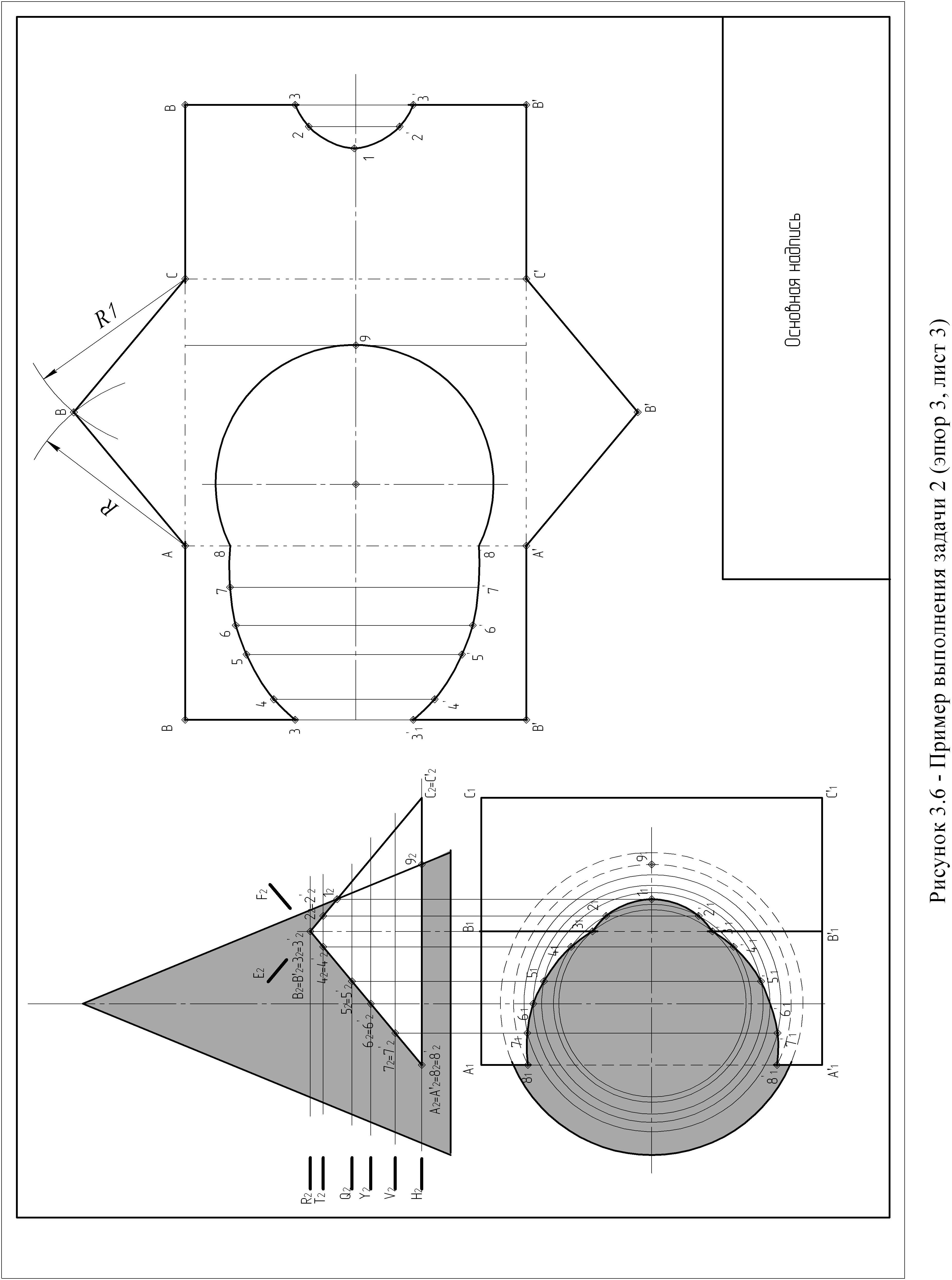
1. В качестве примера рассмотрено пересечение конуса и треугольной призмы. Для построения линии пересечения вводим вспомогательные секущие фронтально – проецирующие плоскости, совпадающие с плоскостями граней призмы. В сечение конуса плоскостью Е получаем часть эллипса, плоскостью F – часть эллипса. Фронтальные проекции фигур сечения совпадают с проекциями граней призмы, поэтому необходимо построить только горизонтальные проекции. Для этого введем вспомогательные горизонтальные плоскости уровня R, T, Q, Y, V, H. Пересечение следов введенных плоскостей с фронтальной проекцией призмы дадут точки, принадлежащие искомой линии пересечения. Точки 3, 3', 8, 8' принадлежат ребрам призмы, точка 1 – контурной образующей конуса, эти точки являются характерными, остальные точки - дополнительными. Построение горизонтальных проекций найденных точек описано в задаче 1.

2. Выполним полную развертку треугольной призмы. На свободном месте проведем вертикальную прямую - ребро ВВ' (его натуральную величину замеряем на горизонтальной плоскости проекции), затем из точек В и В' проводим прямые перпендикулярные ребру ВВ'. На них откладываем длины сторон основания призмы (их натуральную величину замеряем на фронтальной плоскости проекции). Соединяя построенные точки, получаем развертку боковой поверхности призмы. Чтобы развертка стала полной нужно достроить основания призмы. С этой целью проведем из точки А дугу радиусом R = |АВ|, из точки С – R₁ = |ВС| (замеряем на фронтальной плоскости проекции). На пересечении дуг получаем точку В. Второе основание, строится аналогично.

Линия пересечения поверхностей наносится на развертку с помощью ее характерных точек. Для каждой точки определяем прямую принадлежащую грани призмы и параллельную ее ребру. Расстояния от ребра призмы до искомых прямых замеряем на фронтальной плоскости проекции. Затем определяем расстояние от основания призмы до каждой точки. Натуральную величину которого замеряем на горизонтальной плоскости проекции. Соединив полученные точки, построим линии пересечения поверхностей на развертке призмы.

3. Определить видимость проекций линии пересечения и контуров заданных поверхностей

Пример построения показан на рисунке 3.6

Задачи 3, 4 - Пересечение тел вращения

Для определения линии пересечения нужно выбрать наиболее рациональный способ решения. При построении линии пересечения двух поверхностей нужно сначала найти характерные точки искомой кривой:

1. Точки, проекции которых лежат на проекциях контурных линий одной из поверхностей, а также точки, отделяющие видимую часть линии от невидимой;

2. «крайние точки»: правые и левые, наивысшие и наинизшие, ближайшие и наиболее удаленные от плоскостей проекций.

На чертеже обязательно нужно показать построение опорных точек кривой, а также двух-трех промежуточных.

Задача 3 - Построить линию пересечения двух поверхностей способом вспомогательных секущих плоскостей

Вспомогательные секущие плоскости выбирают таким образом, чтобы в пересечении с данными поверхностями они давали наиболее простые линии (окружности, прямые линии). Для всех вариантов заданий в качестве вспомогательных секущих плоскостей могут быть выбраны плоскости уровня: горизонтальные и фронтальные.

Порядок построения:

1. Проводим секущие плоскости H, V, Y, Q, T, R (H₂, V₂, Y₂, Q₂, T₂, R₂) (рисунок 3.7);

2. Находим горизонтальные проекции линий пересечения секущих плоскостей с обеими пересекающимися поверхностями (сечения конуса - окружность, цилиндра - прямоугольник);

3. Находим общие точки пересечения построенных линий;

4. Соединяем последовательно построенные точки и получаем горизонтальную проекцию линию пересечения двух поверхностей;

5. Фронтальная проекция искомой линии будет совпадать с проекцией цилиндра;

6. Определим видимость проекций линии пересечения и контурных образующих заданных поверхностей.

Задача 4 - Построить линию пересечения двух поверхностей методом секущих сфер

Для построения линии пересечения поверхностей вращения с пересекающимися осями и общей плоскостью симметрии применяется способ вспомогательных секущих сфер. В основу этого способа положено свойство сферы пересекать сосную с ней поверхность вращения по окружности. Для того, чтобы вспомогательная секущая сфера пересекала обе поверхности вращения по окружностям, центр сферы должен лежать в точке пересечения осей этих поверхностей.

Порядок построения:

1. Определяем радиус наименьшей сферы - эта сфера должна быть касательной к большей поверхности (рисунок 3.6);

2. Проводим секущую сферу СФ 1;

3. Определяем радиус наибольшей сферы – эта сфера должна проходить через точку пересечения контуров пересекающихся поверхностей, наиболее удаленную от центра впомогательных секущих сфер;

4. Проводим секущую сферу СФ 2;

5. Строим линии пересечения данной сферы с поверхностями вращения (конуса - А2 В2; цилиндра - С2 Д2 и К2 L2);

6. Определяем общие точки при пересечении этих линий 12 и 72;

7. Построив нужное количество сфер, соединим последовательно общие точки и получим линию пересечения двух поверхностей;

8. Строим горизонтальную проекцию линии пересечения, используя линии связи и проекции линий пересечения соответствующей поверхности со сферами. Например, для построения точек 2₁, 2₁',1₁,1₁', необходимо на фронтальной проекции измерить расстояние от оси конуса до точки А₂ (она принадлежит контурной образующей) и в горизонтальной проекции из центра окружности – проекции основания конуса, провести дугу окружности радиусам R, на которую затем спроецировать точки 1₂, 2₂;

9. Определим видимость проекций линии пересечения и контурных образующих данных поверхностей.

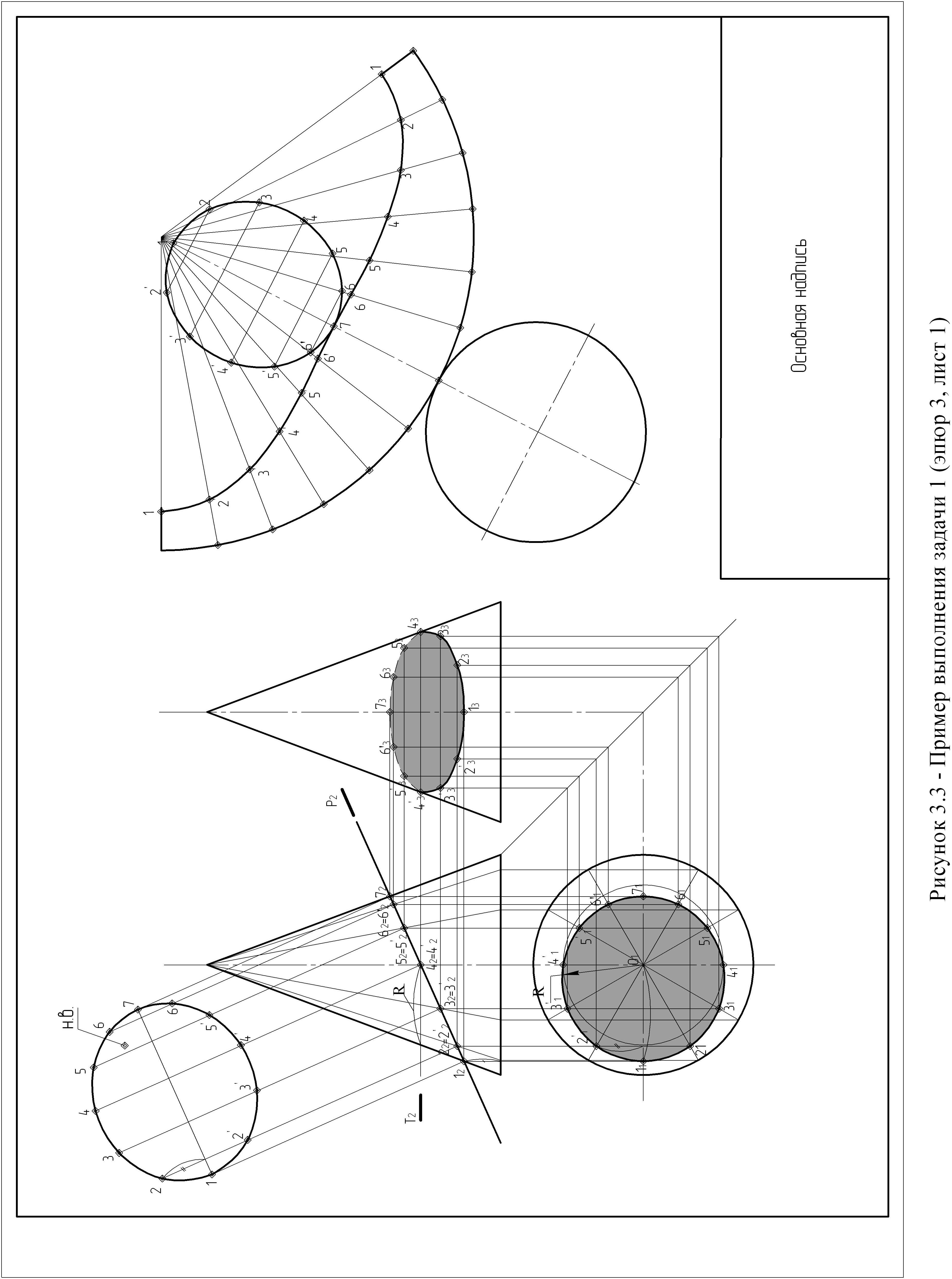
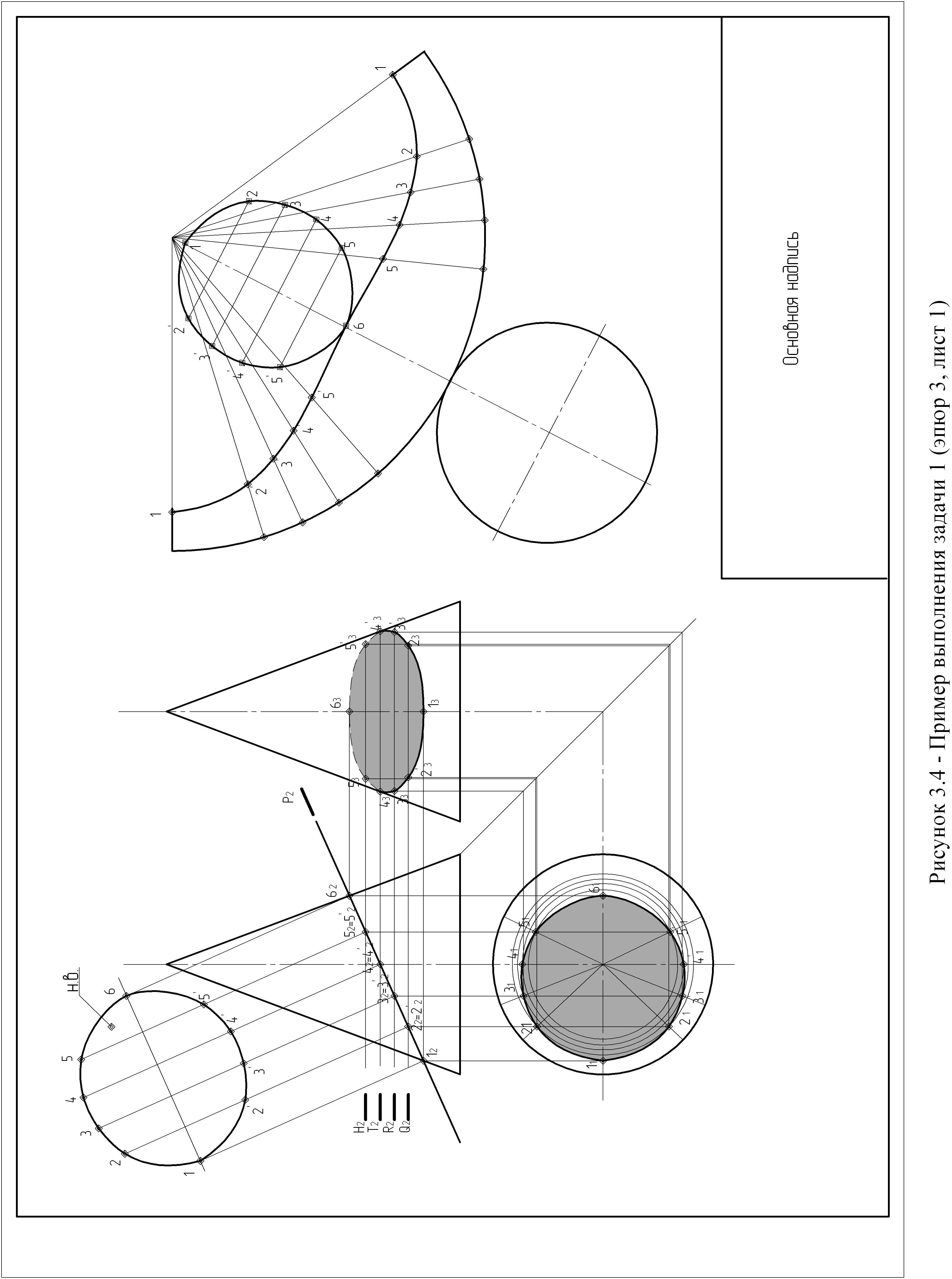
Рисунок 3.5 – Пример выполнения задачи 1 (эпюр 3, лист 2)

ПРИЛОЖЕНИЕ 2