1.2 Порядок выполнения эпюра

Задача 1

В плоскости треугольника {АВС} (рисунок 1.1) через точку С (С₁;С₂) проводим горизонталь (h2, h1) и через точку А (А₁; А₂) - фронталь (f1, f2). Из точки Д опускаем перпендикуляр на плоскость треугольника {АВС}. Для этого из точки Д2 проводим перпендикуляр к фронтальной проекции фронтали f2, а из точки Д1 - перпендикуляр к горизонтальной проекции горизонтали h1 . По теореме прямого угла эти прямые являются фронтальной и горизонтальной проекциями перпендикуляра к плоскости треугольника {АВС}.

Определим точку пересечения построенного перпендикуляра с треугольником {АВС}. Для этого:

1. Через перпендикуляр проведем проецирующую плоскость, в нашем примере - фронтально-проецирующая плоскость Р (фронтальная проекция этой плоскости - Р2);

2. Определяем линию пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника {АВС}. (М₂, N₂) - фронтальная проекция этой линии. По фронтальной проекции прямой (МN) cтроим ее горизонтальную проекцию (М₁, N₁);

3. Определяем точку К₁ - горизонтальную проекцию точки пересечения перпендикуляра с плоскостью треугольника АВС. К₂ - ее фронтальная проекция.

Итак, расстояние от точки Д до плоскости треугольника {АВС} есть отрезок [ДК].

На эпюре построены его проекции [Д₁К₁], [Д₂К₂]. Определим по этим проекциям натуральную величину отрезка [ДК] способом прямоугольного треугольника. Построение выполнено на горизонтальной плоскости проекций П₁. Из точки Д₁ к отрезку [Д₁К₁] восстановлен перпендикуляр, на котором отложен отрезок [Д₁ Д₀], равный разности расстояний точек Д и К до горизонтальной плоскости проекций (Δz замеряем на фронтальной плоскости проекций П₂). Отрезок [К₁ Д₀] есть натуральная величина отрезка [ДК].

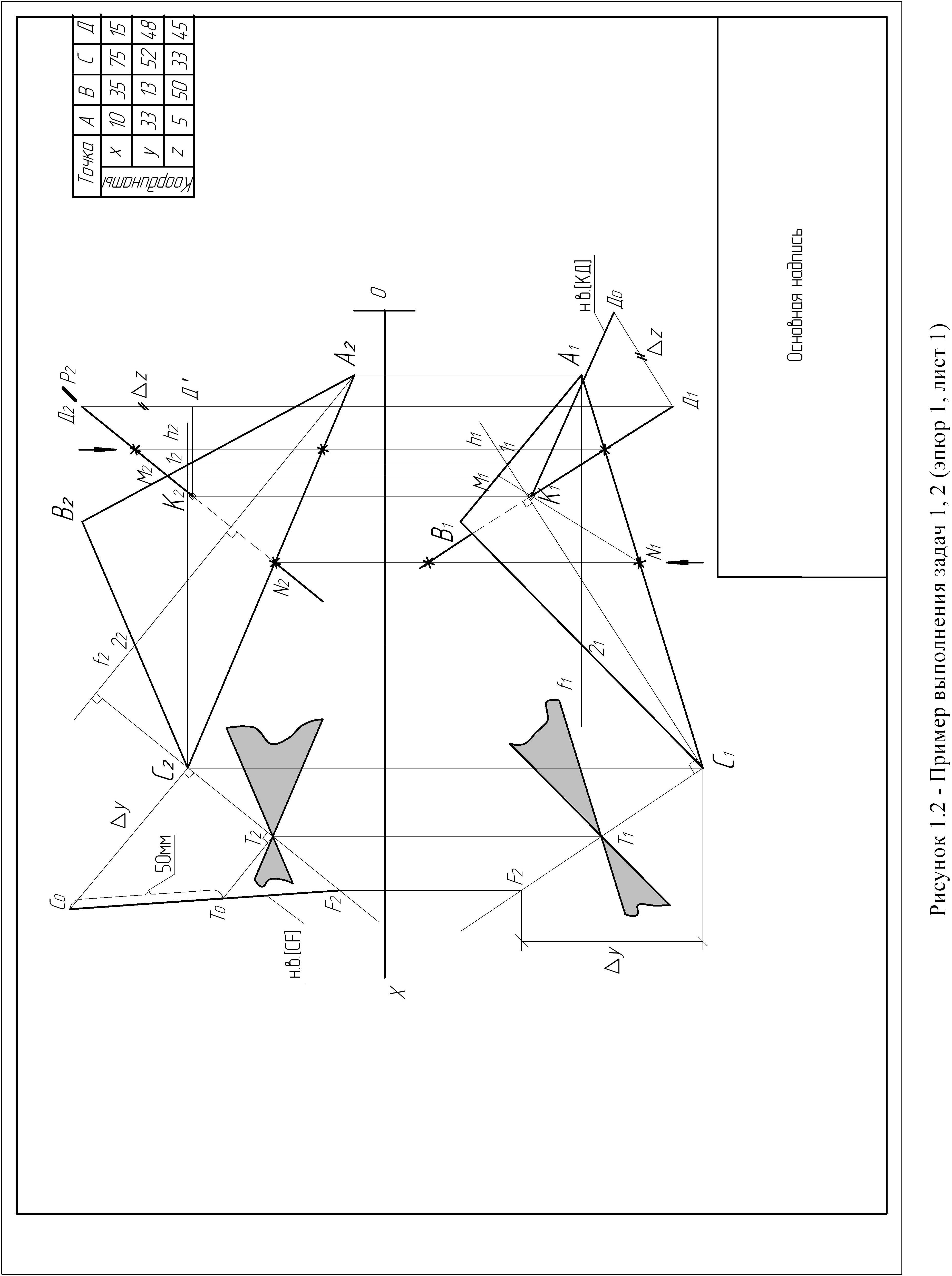
Последним этапом решения данной задачи является определение видимости перпендикуляра относительно данной плоскости. Применим правило определение видимости с помощью конкурирующих точек. Рассмотрим определение видимости в плоскости П₂. Чтобы определить видимость фронтальной проекции перпендикуляра, необходимо в плоскости П₂ выбрать точку наложения проекций перпендикуляра и стороны треугольника (на рисунке 1.2 это проекции (Д₂К₂) и [С₂А₂]) и спроецировать ее на соответствующие прямые в горизонтальную плоскость проекций. Так как точка, находящаяся на отрезке [С₁А₁] ближе к наблюдателю (смотрим снизу), то отрезок [С₂А₂] в плоскости П₂ полностью видим. Значит, проекция перпендикуляра в выбранной нами точке будет невидим. Таким образом, участок перпендикуляра [N₂K₂] невидим, т.к. будет закрыт плоскостью треугольника. Видимость горизонтальной проекции перпендикуляра определяется аналогично (рисунок 1.2).

Таким образом, первая задача решена.

Задача 2

Из вершины треугольника, в нашем примере из точки С (рисунок 1.2), восстанавливаем перпендикуляр к плоскости треугольника {АВС}. На проекциях: из точки С2 - перпендикуляр к фронтальной проекции фронтали f2, из точки С1 - перпендикуляр к горизонтальной проекции горизонтали h1. На перпендикуляре берем произвольную точку F (F1, F2) и определяем натуральную величину отрезка [СF].

На отрезке [С₀ F₂] от точки С₀ откладываем 50 мм (точка Т0) и находим точку Т (Т1, Т2), отстоящую от плоскости треугольника {АВС} на 50 мм. Две прямые, пересекающиеся в этой точке, проведенные параллельно двум сторонам треугольника {АВС} (на фронтальной и горизонтальной плоскостях проекций), определяют плоскость, параллельную плоскости треугольника {АВС} и отстоящую от последней на 50 мм. Вторая задача решена.

Задача 3

Из точки В2 к стороне [А2С2] проводим перпендикуляр (рисунок 1.3). По теореме прямого угла он должен явиться фронталью (фронтальная проекция f2). Горизонтальная проекция фронтали f1 выходит из точки В1 параллельно оси Х.

Из точки В1 опускаем перпендикуляр к стороне [А1С1] . Соответствено, он должен явиться горизонталью - h1 , h2 || Х.

Точки F и E на перпендикулярах берем произвольно. Итак, треугольник {BEF}, перпендикулярный треугольнику {АВС}, построен.

Определим линию пересечения этих треугольников. Две плоскости пересекаются по прямой. Прямую определяют две точки. Первая общая точка - точка В. Вторую общую точку (на рисунке 1.3 это точка К) найдем в пересечении прямой (ЕF) c плоскостью треугольника {АВС}. Для этого через прямую (EF) проведем вспомогательную фронтально-проецирующую плоскость Р (фронтальная проекция Р2). Определим линию пересечения плоскости Р с плоскостью треугольника {АВС}. (M₂N₂) – фронтальная проекция этой линии, (M₁N₁) – горизонтальная. Далее находим точки К₁ и К₂. Соединив точки В и К (В₂ и К₂, В₁ и К₁ на проекциях), получим искомую линию пересечения. Остается определить видимость треугольника. Для этого необходимо воспользоваться правилом определения видимости с помощью конкурирующих точек. Чтобы определить видимость горизонтальных проекций треугольников, нужно в плоскости П₁ выбрать точку наложения проекций сторон треугольников (на рисунке 1.2 это проекции сторон EF и AC) и спроецировать ее на соответствующие прямые во фронтальную плоскость. Так как точка, находящаяся на стороне (E₂F₂) ближе к наблюдателю (смотрим сверху), то сторона (E₁F₁) видима до точки К₁ на горизонтальной проекции. Так как прямая EF на участке (E₁К₁) видима, то проекция (A₁C₁) в выбранной нами точке (_*) будет невидима и, следовательно, (A₁C₁) будет закрыта проекцией треугольника BEF, этот участок прямой (A₁C₁) показан штриховой линией. Тогда (В₁Е₁) видима полностью. Проекция (F₁B₁) вообще не пересекается с Δ А₁В₁С₁, поэтому тоже видима.

Видимость фронтальных проекций треугольников определяется аналогично (рисунок 1.3).

Третья задача решена полностью.

Таблица 1 - Индивидуальные задания к эпюру 1.

№ вар.	Точки	Координаты			№ вар.	Точки	Координаты
		х	у	z			х	у	z
1	2	3			4	5	6
1	А В С Д	65 10 0 35	10 20 60 70	20 0 60 5	11	А В С Д	65 20 0 60	20 5 50 55	55 5 25 10
2	А В С Д	70 45 0 20	0 50 20 50	60 10 10 55	12	А В С Д	75 35 0 65	5 55 25 55	25 65 0 0
3	А В С Д	70 40 0 65	60 0 45 15	45 55 10 0	13	А В С Д	65 10 0 35	20 0 60 5	10 20 60 70
4	А В С Д	65 40 0 70	20 5 50 65	0 55 5 55	14	А В С Д	70 45 0 20	60 10 10 55	0 50 20 50
5	А В С Д	65 45 0 10	60 15 5 45	10 55 25 55	15	А В С Д	70 40 0 65	45 55 10 0	60 0 45 15
6	А В С Д	60 45 5 70	65 20 10 20	20 50 10 10	16	А В С Д	65 40 0 70	0 55 5 55	20 5 50 65
7	А В С Д	65 40 0 55	15 0 40 60	0 55 20 50	17	А В С Д	60 45 0 10	10 55 25 55	60 15 5 45
8	А В С Д	60 45 5 75	65 10 10 15	30 60 20 10	18	А В С Д	60 45 5 70	20 50 10 10	65 20 10 20
9	А В С Д	75 30 10 60	25 5 60 55	0 50 20 55	19	А В С Д	65 40 0 55	0 55 20 50	15 0 40 60
10	А В С Д	80 45 0 10	20 0 45 0	10 70 40 15	20	А В С Д	60 45 5 75	30 60 20 10	65 10 10 15

Продолжение таблицы 1

1	2	3			4	5	6
		х	у	z			х	у	z
21	А В С Д	75 30 10 60	0 50 20 55	25 5 60 55	31	А В С Д	65 40 0 55	25 10 50 70	10 65 30 60
22	А В С Д	80 45 0 10	10 70 40 15	20 0 45 0	32	А В С Д	60 45 5 75	75 20 20 25	40 70 30 20
23	А В С Д	65 25 0 60	55 5 25 10	20 5 50 55	33	А В С Д	75 30 10 60	35 15 70 65	10 60 30 65
24	А В С Д	75 35 0 65	25 65 0 0	5 55 25 55	34	А В С Д	80 45 0 10	30 10 55 10	20 80 50 25
25	А В С Д	65 10 0 35	20 30 70 70	30 10 70 15	35	А В С Д	65 20 0 60	30 15 60 65	65 15 35 20
26	А В С Д	70 45 0 20	10 60 30 60	70 20 20 65	36	А В С Д	75 35 0 65	15 65 35 65	35 75 10 10
27	А В С Д	70 40 0 65	70 10 55 25	55 65 20 10	37	А В С Д	65 10 0 35	30 10 70 15	20 30 70 80
28	А В С Д	65 40 0 70	30 15 60 75	10 65 15 65	38	А В С Д	70 45 0 20	70 20 20 65	10 60 30 60
29	А В С Д	60 45 0 10	70 25 15 55	20 65 35 65	39	А В С Д	70 40 0 65	55 65 20 10	70 10 55 25
30	А В С Д	65 45 5 70	75 30 20 30	30 60 20 20	40	А В С Д	65 40 0 70	10 65 15 65	30 15 65 75

Продолжение таблицы 1

1	2	3			4	5	6
		х	у	z			х	у	z
41	А В С Д	60 45 0 10	20 65 35 65	70 25 15 55	51	А В С Д	80 50 10 75	60 0 45 15	45 55 10 0
42	А В С Д	60 45 5 70	30 60 20 20	75 30 20 30	52	А В С Д	75 50 10 80	20 5 50 65	0 55 5 55
43	А В С Д	65 40 0 55	10 65 30 60	25 10 50 70	53	А В С Д	70 55 10 20	60 15 5 45	10 55 25 55
44	А В С Д	60 45 5 75	40 70 30 20	75 20 20 25	54	А В С Д	70 55 15 80	65 20 10 20	20 50 10 10
45	А В С Д	75 30 10 60	10 60 30 65	35 15 70 65	55	А В С Д	75 50 10 65	15 0 40 60	0 55 20 50
46	А В С Д	80 45 0 10	20 80 50 25	30 0 55 10	56	А В С Д	70 55 15 85	65 10 10 15	30 60 20 10
47	А В С Д	65 25 0 60	65 15 35 20	30 15 60 65	57	А В С Д	85 40 20 70	25 5 60 55	0 50 20 55
48	А В С Д	75 35 0 65	35 75 10 10	15 65 35 65	58	А В С Д	90 55 10 20	20 0 45 0	10 70 40 15
49	А В С Д	75 20 10 45	10 20 60 70	20 0 60 5	59	А В С Д	75 30 10 70	20 5 50 55	55 5 25 10
50	А В С Д	80 55 10 30	0 50 20 50	60 10 10 55	60	А В С Д	85 45 10 75	5 55 25 55	25 65 0 0

Продолжение таблицы 1

1	2	3			4	5	6
		х	у	z			х	у	z
61	А В С Д	75 20 10 45	20 0 60 5	10 20 60 70	64	А В С Д	75 50 10 80	0 55 5 55	20 5 50 65
62	А В С Д	80 55 10 30	60 10 10 55	0 50 20 50	65	А В С Д	70 5 10 20	10 55 25 55	60 15 5 45
63	А В С Д	80 50 10 75	45 55 10 0	60 0 45 15	66	А В С Д	70 55 15 80	20 50 10 10	65 20 10 20