Эпюр № 2 по теме « Способы преобразования проекций »

2.1. Содержание эпюра:

Дано: Координаты вершин пирамиды SABC.

Требуется:

задача 1 - определить натуральную величину основания пирамиды АВС.

задача 2 - определить расстояние от вершины пирамиды S до плоскости ее основания АВС.

задача 3 - найти кратчайшее расстояние между ребрами пирамиды SА и ВС.

задача 4 - определить величину двугранного угла при ребре пирамиды АВ.

Рекомендации по выполнению эпюра:

1. Чертеж должен быть выполнен в соответствии с ГОСТми: 2.301 – 68^* (Форматы), 2.302 - 68^* (Масштабы), 2.303 - 68^* (Линии), 2.304 – 81 (Шрифты) (приложение 4);

2. После выполнения чертежа выполнить его обводку (возможно оформление в цвете):

• исходный чертеж (цвет черный) и результат построений (цвет красный) выполнить сплошными основными толстыми линиями;

• промежуточные построения (цвет синий) – сплошными тонкими;

• невидимые линии – штриховой.

Указания к выполнению эпюра:

1. Студенты факультета МСХ выполняют задачи 1 – 4 на двух форматах А3. Задачи 1, 2 совместить на первом листе эпюра, задачи 3, 4 – на втором. Студенты факультета ПГС выполняют задачи 1 – 3 на двух форматах А3.

2. Данные для выполнения эпюра взять из таблицы 2 в соответствии с вариантом. Координаты точек даны в миллиметрах. Все задания выполнить в масштабе 1:1. Основная надпись выбирается в соответствии с факультетом из приложения 3.

Задачи эпюра должны быть решены следующими способами:

- плоскопараллельное перемещение (задача 2);

- вращение вокруг горизонтали или фронтали (задача 1);

- замена плоскостей проекций (задачи 3, 4).

Примечание: при решении задач 3 и 4 расстояния переносимые из одной плоскости в другую отмечать засечками или другими знаками (рисунки 2.8, 2.9).

Внимание! Не разрешается все задачи решать одним способом.

2.2. Порядок выполнения эпюра

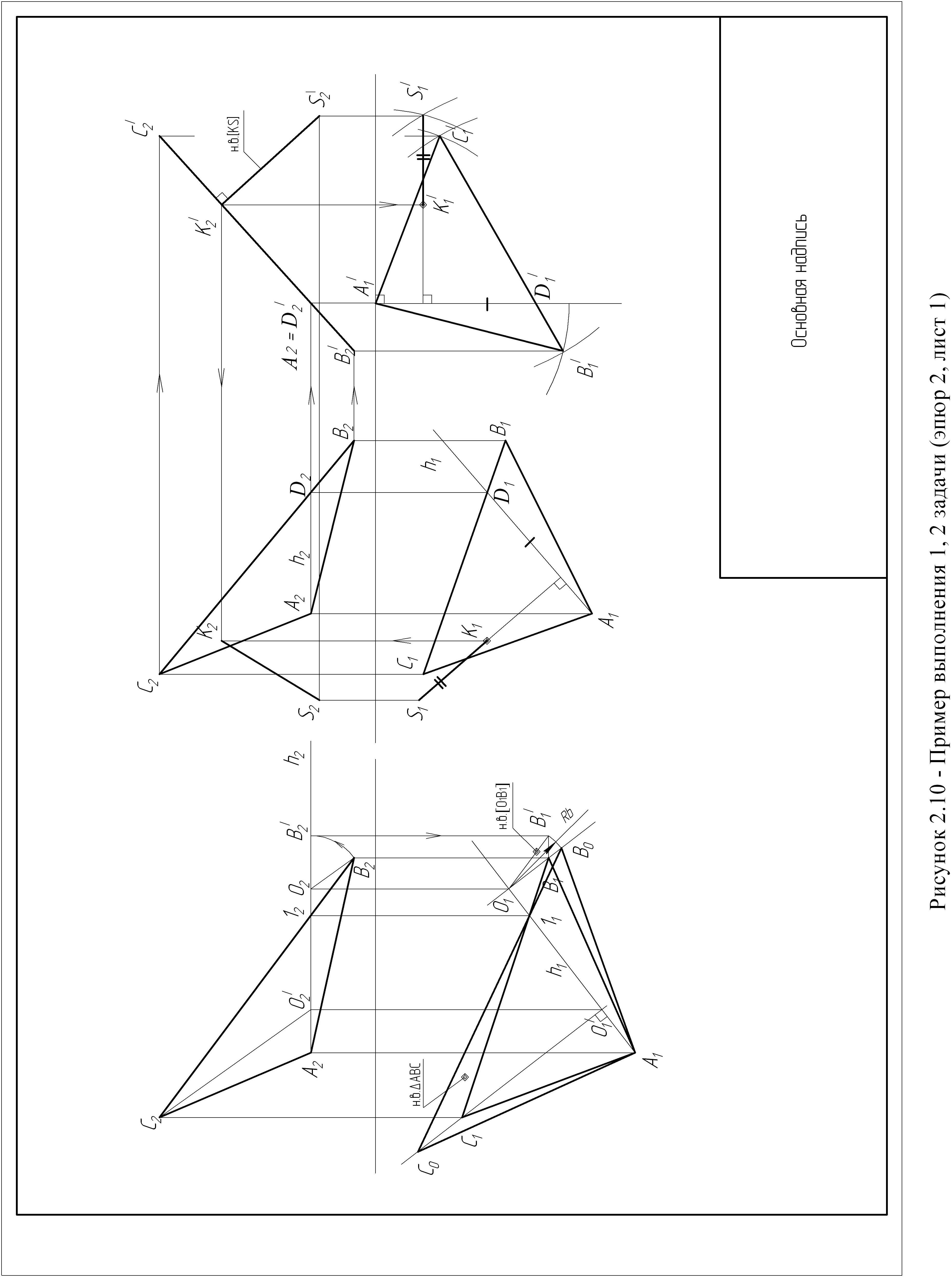
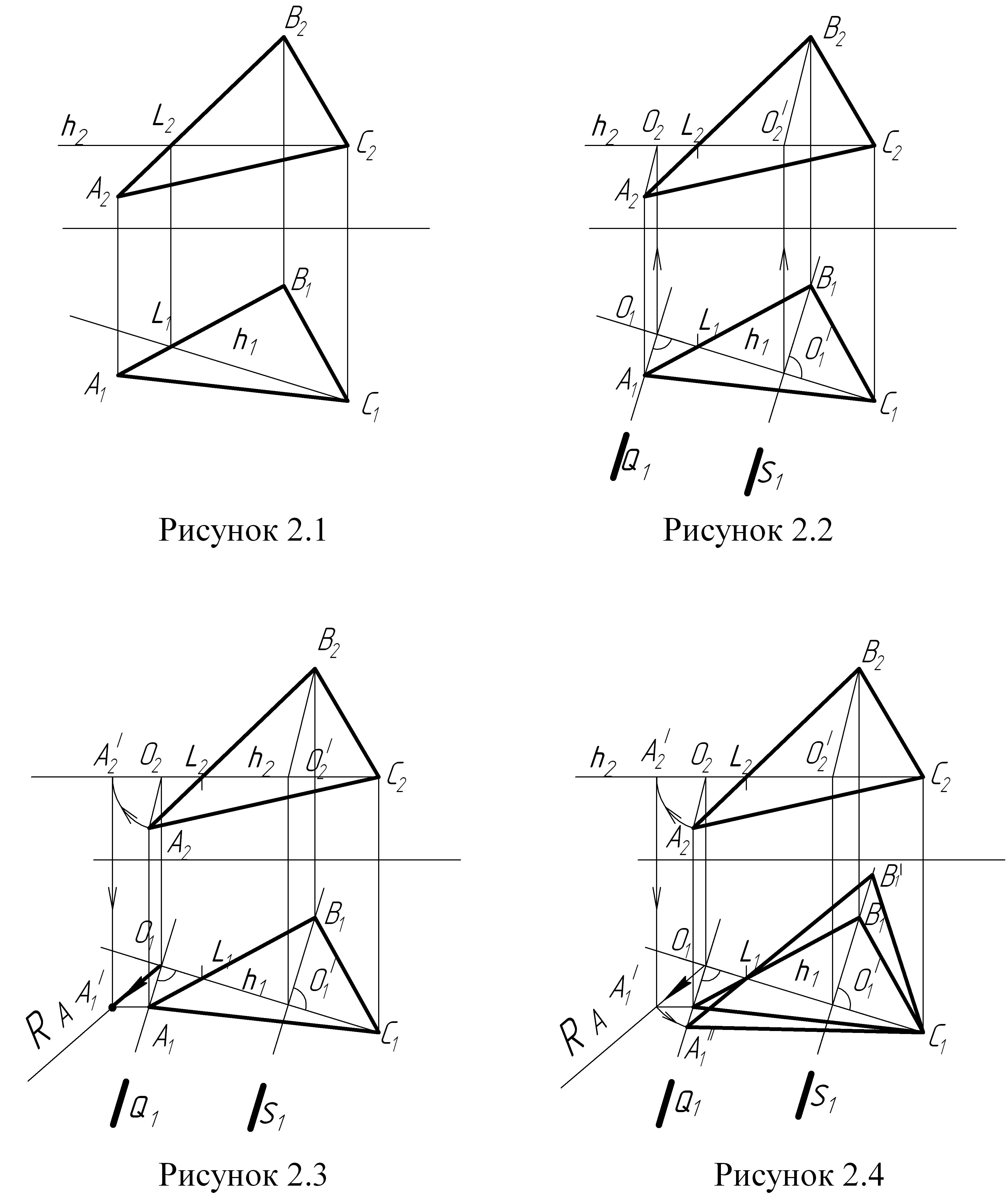
Задача 1 (рисунки 2.1, 2.2, 2.3, 2.4)

Для решения задачи 1 необходимо преобразовать чертеж так, чтобы основание пирамиды (треугольник {АВС}), представляющее собой плоскость общего положения, в результате вращения оказалось параллельным одной из плоскостей проекций.

За ось вращения принимаем горизонталь СL (С₂L₂, С₁L₁). Каждая точка треугольника {АВС}, вращаясь вокруг горизонтали СL, будет описывать дугу окружности в плоскости, перпендикулярной к этой горизонтали, а следовательно, и к плоскости П₁.

Окружности, которые описывают вершины А и В треугольника АВС, находясь в горизонтально – проецирующих плоскостях Q и S, спроецируются на плоскость П₁ в виде прямых, совмещенных со следами Q₁ и S₁ плоскостей Q и S.

Центры вращения точек А и В будут лежать на оси вращения (горизонтали CL). Для вершины А– точка О ( О₁,О₂ ), для вершины В – точка О´( О₁´,О₂´ ).

Когда плоскость треугольника АВС будет параллельна плоскости П₁, горизонтальная проекция каждой из перемещающихся вершин окажется удаленной от оси вращения (горизонтали СL) на расстояние, равное радиусу вращения данной точки.

Порядок построения:

1. По координатам точек А, В, С строим проекции треугольника {АВС};

2. В плоскости треугольника {АВС} проводим горизонталь СL (С₂L₂, С₁L₁) являющуюся осью вращения треугольника {АВС} ( рисунок 2.1 );

3. Из горизонтальных проекций вершин А и В проводим прямые, перпендикулярные горизонтали СL, по которым будут перемещаться горизонтальные проекции вращающихся точек ( рисунок 2.2);

4. Отмечаем проекции центров вращения вершин треугольника. Для вершины А–точка О ( О₁,О₂ ), для вершины В – точка О´( О₁´,О₂´ ). Радиус вращения вершины А – [АО] ([А₁О₁], [А₂О₂]), радиус вращения вершины В – [ВО'] ([В₁О₁'], [В₂О₂']);

5. По двум проекциям определяем натуральную величину R_А радиуса вращения вершины А (рисунок 2.3). Натуральная величина R_А определяется способом вращения отрезка [АО] вокруг оси , проходящей через точку О перпендикулярно плоскости П₂;

6. Отрезок R_А откладываем от точки О₁ вдоль прямой, по которой перемещается горизонтальная проекция вершины А₁. Получим точку А₁'';

7. Через полученную точку В₁' и точку L₁ проводим прямую до пересечения с прямой, по которой перемещается горизонтальная проекция вершины В;

8. Получим точку В₁' ( рисунок 2.4);

9. Соединяя найденные точки А₁'' и В₁' с вершиной С₁ , получаем новую горизонтальную проекцию треугольника {А₁''В₁'С₁}. Эта проекция определяет натуральную величину плоскости треугольника {АВС}.

Задача 2 (рисунки 2.5, 2.6)

Для решения задачи 2 необходимо преобразовать чертеж так, чтобы основание пирамиды – треугольник {АВС}, представляющий собой плоскость общего положения, в результате перемещения оказалось перпендикулярным плоскости П₂ (плоскости П₁), т.е. стало фронтально – проецирующей плоскостью (горизонтально – проецирующей плоскостью).

Порядок построения:

1. По координатам точек S, A, B, C строим проекции основания пирамиды треугольника {АВС} и ее вершину точки S;

2. В плоскости треугольника {АВС} проводим горизонталь ВД (В₁Д₁, В₂Д₂) (рисунок 2.5);

3. По координатам точек S, A, B, C строим проекции основания пирамиды треугольника {АВС} и ее вершину точки S;

4. В плоскости треугольника {АВС} проводим горизонталь ВД (В₁Д₁, В₂Д₂) (рисунок 2.5);

5. Переместим треугольник {АВС} так, чтобы горизонтальная проекция В₁Д₁ горизонтали заняла положение перпендикулярное оси Х, а фронтальная проекция треугольника {А₂В₂С₂} превратилась в прямую линию, т.е. треугольник {АВС} станет фронтально - проецирующей плоскостью;

6. Найдем новое положение точки S (при помощи засечек);

7. Перпендикуляр из точки S к фронтально проецирующей плоскости будет искомым расстоянием (рисунок 2.6);

8. Покажем перпендикуляр [SК] в исходных проекциях;

9. Определить видимость перпендикуляра [SK].

Примечание: задачу можно решать, преобразовав треугольник АВС в горизонтально – проецирующую плоскость, тогда в плоскости треугольника необходимо построить фронталь.

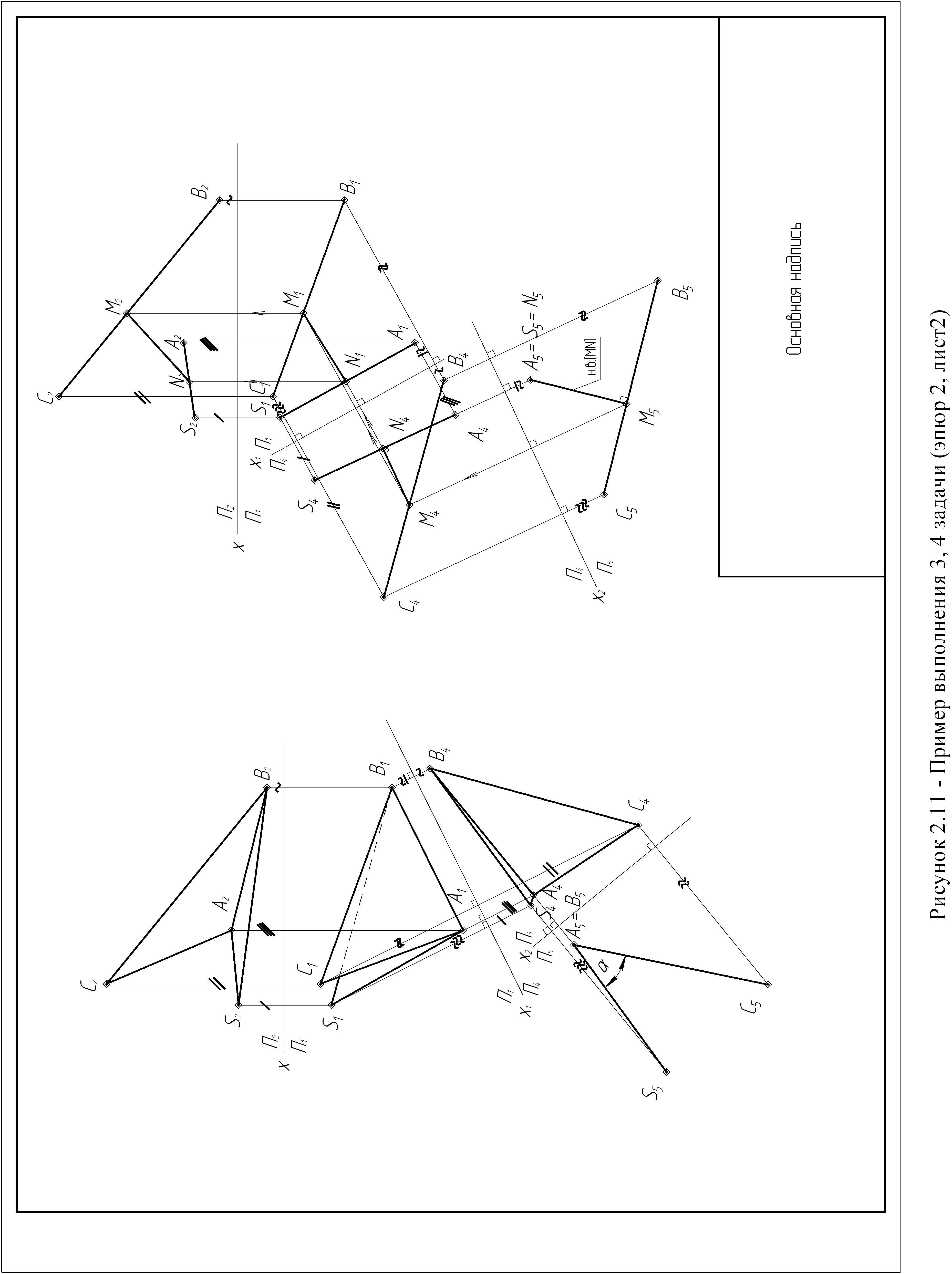
Задача 3 (рисунки 2.7, 2.8, 2.9)

Если одна из заданных прямых является проецирующей прямой, то кратчайшее расстояние между такими прямыми измеряется длиной перпендикуляра [MN], общего к заданным прямым. В этом случае перпендикуляр [MN] будет параллелен одной из плоскостей проекций и равен длине его проекции на эту плоскость.

Для решения данной задачи необходимо одну из прямых общего положения (SA) или (BC) преобразовать в прямую проецирующую, применив две замены плоскостей проекций.

Порядок построения:

1. По координатам точек S, A, B, C построить проекции ребра пирамиды SA и проекцию стороны основания BC (рисунок 2.7);

2. При первой замене чертеж преобразуем так, чтобы прямая общего положения (ВС) оказалась параллельной одной из плоскостей проекций, для этого вводим новую плоскость П₄, перпендикулярную плоскости П₁ и параллельную отрезку [ВС]. Ось Х₁ проведем параллельно [В₁С₁]. Измеряя расстояния от оси х до точек А₂, S₂, В₂ и С₂ и откладывая их в плоскости П₄ от оси х₁, получаем проекции [S₄A₄] и [В₄C₄] прямых (SA) и (ВС) (рисунок 2.8);

3. При второй замене чертеж преобразуем так, чтобы отрезок прямой [ВС], параллельный в системе П₄/П₁ плоскости П₄, стал перпендикулярен плоскости П₅ в системе П₄/П₅ (рисунок 2.9);

4. Вводим новую плоскость П₅, перпендикулярно плоскости П₄ и отрезку [ВС], т.е. ось Х₂ пройдет перпендикулярно [В₄С₄]. Измерив расстояния от оси Х₁ до точек А₁, S₁, В₁, С₁ и отложить их в плоскости П₅ от оси Х₂ на соответствующих линиях связи, получим проекции [В₅С₅] и [S₅А₅];

5. Находим кратчайшее расстояние [МN] между прямыми (SА) и (ВС). Кратчайшим расстоянием будет являться перпендикуляр, опущенный из точки В₅=С₅ на проекцию [S₅А₅];

6. По линиям связи находим проекции кратчайшего расстояния между прямыми (SА) и (ВС) в исходных проекциях.

Примечание: данную задачу можно решить, используя только одну замену плоскостей проекций, если одна из данных прямых (AS) или (BC) является прямой уровня.

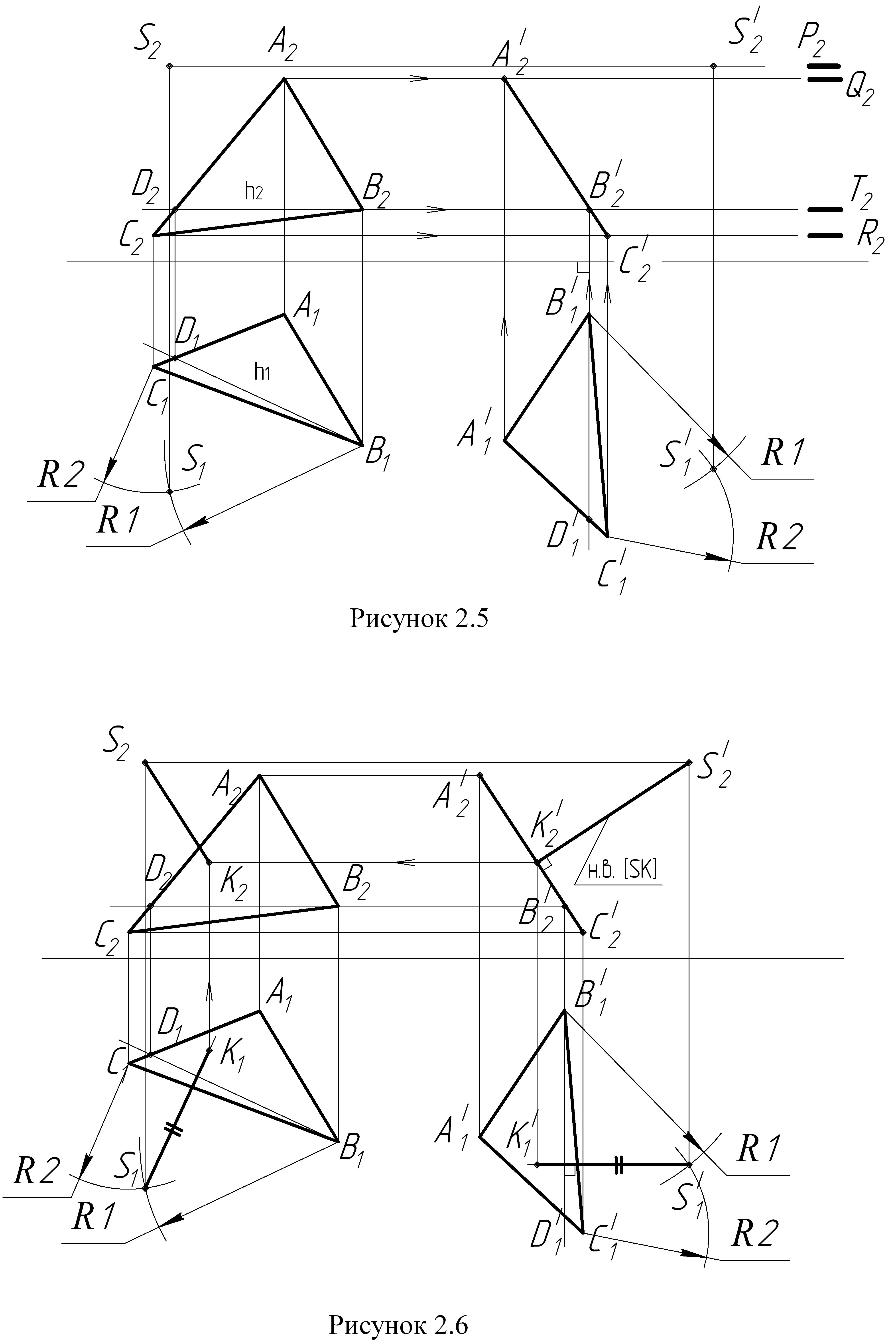
Задача 4

Если двугранный угол образован проецирующими плоскостями и ребро АВ двугранного угла перпендикулярно этой плоскости, то двугранный угол спроецируется в натуральную величину.

Для решения данной задачи необходимо ребро АВ (прямую общего положения) преобразовать в проецирующую прямую, применив две замены плоскостей проекций.

Порядок построения:

1. По координатам точек S, А, В, С строим проекции двугранного угла;

2. При первой замене чертеж преобразуем так, чтобы ребро АВ двугранного угла оказалось параллельным одной из плоскостей проекций, т.е. вводим новую плоскость П₄, перпендикулярно плоскости П₂ и параллельно ребру АВ; ось Х₁ пройдет параллельно [А₁В₁] (рисунок 2.11);

3. По линиям связи, перпендикулярным оси Х₁, двугранный угол проецируем на плоскость П₄. Получаем проекцию S₄А₄В₄С₄ двугранного угла SАВС.

4. При второй замене чертеж преобразуем так, чтобы ребро АВ стало перпендикулярно новой плоскости П₅;

5. Вводим новую плоскость П₅ перпендикулярно плоскости П₄ и ребру АВ, т.е. ось Х₂ пойдет перпендикулярно А₄В₄. По линиям связи, перпендикулярным оси Х₂, проецируем двугранный угол SАВС на плоскость П₅. Получаем проекцию двугранного угла на плоскости П₅;

6. Натуральной величиной двугранного угла будет угол α, между проекциями сторон двугранного угла [А₅=В₅ S₅] и [А₅=В₅ С₅].

Примечание: если ребро АВ двугранного угла является прямой уровня, то задача решается с помощью одной замены плоскостей проекций.

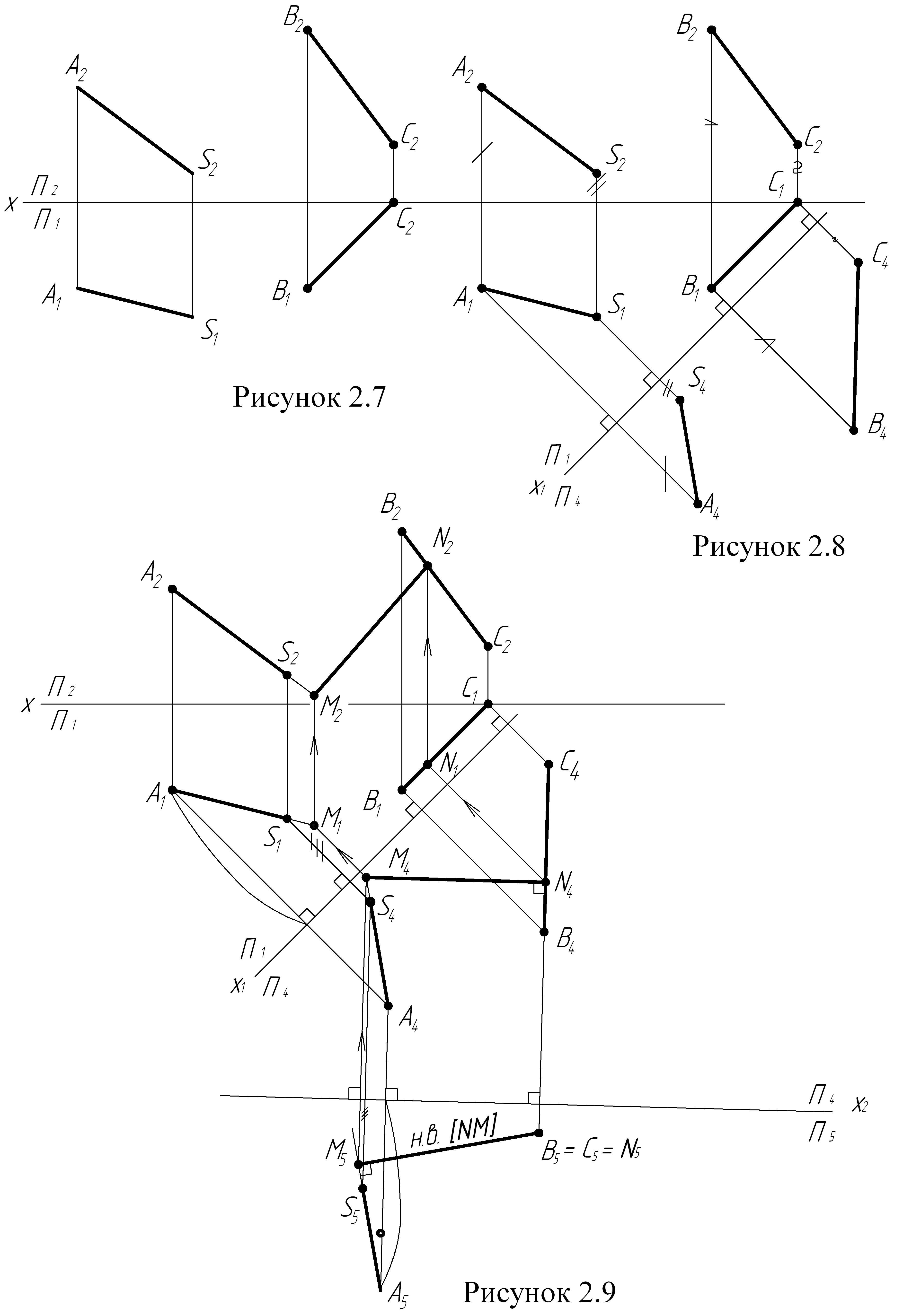
Таблица 2 - Индивидуальные задания к эпюру 2.

№ вар.	Точки	Координаты			№ вар.	Точки	Координаты
		х	у	z			х	у	z
1	S А В С	65 45 5 70	65 5 45 15	50 55 10 0	11	S А В С	20 10 55 80	50 20 50 0	45 10 10 60
2	S А В С	35 65 0 10	60 0 50 10	5 20 60 0	12	S А В С	65 75 5 55	0 20 10 50	40 0 15 30
3	S А В С	55 35 5 60	10 65 25 30	50 35 10 5	13	S А В С	65 45 5 70	50 55 10 0	65 5 45 15
4	S А В С	10 80 45 0	0 20 0 45	15 10 70 40	14	S А В С	35 65 0 10	5 20 60 0	60 0 50 10
5	S А В С	70 40 0 65	65 5 50 20	35 55 10 0	15	S А В С	55 35 5 60	50 35 10 5	10 60 25 30
6	S А В С	70 75 35 10	50 15 0 45	5 50 0 20	16	S А В С	10 80 45 0	15 10 70 40	0 20 0 45
7	S А В С	60 75 30 10	45 25 15 50	55 0 50 20	17	S А В С	70 40 0 65	55 55 10 0	65 5 50 20
8	S А В С	75 45 0 60	25 20 10 65	10 60 20 20	18	S А В С	70 75 35 10	5 50 0 20	50 15 0 45
9	S А В С	75 60 45 5	25 65 10 10	20 20 60 20	19	S А В С	60 75 30 10	55 0 50 20	45 25 15 50
10	S А В С	60 45 0 60	10 15 5 60	20 55 25 10	20	S А В С	75 45 0 60	25 60 20 30	20 20 10 65

Продолжение таблицы 2

1	2	3			4	5	6
		х	у	z			х	у	z
21	S А В С	75 60 45 5	10 20 60 20	25 65 10 10	31	S А В С	60 40 0 65	65 5 45 15	50 55 10 0
22	S А В С	60 45 0 60	20 55 25 10	10 15 5 60	32	S А В С	70 40 0 55	25 20 10 65	10 60 20 20
23	S А В С	20 10 55 80	45 10 10 60	50 20 50 0	33	S А В С	70 55 40 0	25 65 10 10	20 20 60 20
24	S А В С	65 75 5 55	45 0 15 30	0 20 10 50	34	S А В С	55 40 0 55	10 15 5 60	20 55 25 10
25	S А В С	60 40 0 65	65 5 45 15	50 55 10 0	35	S А В С	15 5 50 75	50 20 50 0	45 10 10 60
26	S А В С	30 60 0 5	60 0 50 10	5 20 60 0	36	S А В С	60 70 0 50	0 20 10 50	40 0 15 30
27	S А В С	50 30 0 55	10 60 25 30	50 35 10 5	37	S А В С	60 40 0 65	55 40 0 55	65 5 45 15
28	S А В С	5 75 40 0	0 20 0 45	15 10 70 40	38	S А В С	30 60 0 5	5 20 60 0	60 0 50 10
29	S А В С	65 35 0 60	65 5 50 20	35 55 10 0	39	S А В С	50 30 0 55	50 35 10 5	10 60 25 30
30	S А В С	65 70 30 5	50 15 0 45	5 50 0 20	40	S А В С	5 75 40 0	15 10 70 40	0 20 0 45

Продолжение таблицы 2

1	2	3			4	5	6
		х	у	z			х	у	z
41	S А В С	65 35 0 60	55 55 10 0	65 5 50 20	51	S А В С	50 35 5 60	10 60 25 30	50 35 10 5
42	S А В С	65 70 30 5	5 50 0 20	50 15 0 45	52	S А В С	5 80 45 0	0 15 0 40	15 10 70 40
43	S А В С	55 70 25 5	55 0 50 20	45 25 15 50	53	S А В С	65 40 0 65	60 0 45 15	35 55 10 0
44	S А В С	70 40 0 55	25 60 20 30	20 20 10 65	54	S А В С	65 75 35 10	45 10 0 40	5 50 0 20
45	S А В С	70 55 40 5	10 20 60 20	25 65 10 10	55	S А В С	5 70 25 10	40 20 10 45	55 0 50 20
46	S А В С	55 40 0 55	20 55 25 10	10 15 5 60	56	S А В С	70 45 0 60	20 15 5 60	10 60 20 20
47	S А В С	15 5 50 75	45 10 10 60	50 20 50 0	57	S А В С	70 60 45 5	20 60 5 5	20 20 60 20
48	S А В С	60 70 0 50	45 0 15 30	0 20 10 50	58	S А В С	55 45 0 60	5 10 0 55	20 55 25 10
49	S А В С	60 45 5 70	60 0 40 10	50 55 10 0	59	S А В С	15 10 55 80	45 15 45 0	45 10 10 60
50	S А В С	30 65 0 10	55 0 45 5	5 20 60 0	60	S А В С	60 45 5 70	45 50 5 0	65 5 45 15

Продолжение таблицы 2

1	2	3			4	5	6
		х	у	z			х	у	z
61	S А В С	30 65 0 10	0 15 55 0	60 0 50 10	64	S А В С	65 40 0 65	50 50 5 0	65 5 50 20
62	S А В С	50 35 5 60	45 30 5 5	10 60 25 30	65	S А В С	65 75 35 10	0 45 0 15	50 15 0 45
63	S А В С	5 80 45 0	10 5 65 35	0 20 0 45	66	S А В С	55 75 30 10	50 0 45 15	45 25 15 50