§ 4.5. Евклидовы пространства

Введение скалярного произведения Свойства векторов в евклидовом пространстве Ортонормированная система векторов Ортогональное дополнение Линейные многообразия в евклидовом пространстве

Введение скалярного произведения

Введенное нами линейное векторное пространство не содержит информации о том, как измерять длины и углы в этом пространстве. Неожиданным на первый взгляд является возможность решить этот вопрос, если ввести понятие скалярного произведения.

Пусть любым двум векторам и из ставится в соответствие число, обозначаемое как , причем выполняются следующие условия:

1) ;

2) ;

3) , где ;

4) , если - ненулевой вектор; , если - нулевой вектор.

Назовем это число скалярным произведением.

Пусть векторы и задаются набором своих координат в некотором базисе

, .

Подстановка этих разложений в скалярное произведение с последующим применением аксиом 2) и 3) дает формулу

Выражение в правой части равенства можно представить в виде произведения матриц

.

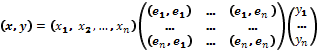или в сокращенном виде ,

где матрица

называется матрицей Грама, , .

Свойства матрицы Грама.

1. Матрица Грама существует для базиса из , поскольку существуют числа ), где . Матрица Грама как квадратная при любом наборе векторов имеет определитель.

2. Матрица Грама является симметричной матрицей. Действительно, первая аксиома позволяет векторы переставлять в скалярном произведении местами ).

3. Транспонирование матрицы не приводит к ее изменению 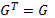. Это следует непосредственно из симметричности.

4. Если векторы линейно независимы, определитель матрицы Грама положителен 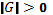, при линейной зависимости векторов – равен нулю . Доказательство будет дано ниже.

Скалярное произведение лежит в основе определения евклидова пространства и часто используется. В связи с этим желательно базисы в евклидовом пространстве выбирать так, чтобы процедура вычисления скалярного произведения была простой. Наиболее удачный вариант реализуется, если векторы удастся подобрать исходя из условия

(11)

Ниже мы покажем, что это возможно. Матрица Грама превращается в единичную, а скалярное произведение становится равным

. (12)

Заданное таким образом число для случая или обращается в рассмотренное ранее скалярное произведение геометрических векторов.

Теперь появляется возможность определить длины и углы в пространстве. Введем модуль вектора в векторном пространстве

.

Пусть , тогда

. (13)

Выражение было введено в §4.4 «Метрические пространства» как формула метрики . Она - одна из возможных метрик - делает линейное векторное пространство метрическим, поскольку для все аксиомы метрики выполнены. Записанная в координатах, формула (13) совпадает с так называемой «евклидовой нормой».

В частном случае расстояние между вектором и нулевым вектором было определено как норма вектора

= . (14)

Таким образом, введение скалярного произведения векторов в векторном пространстве с дополнительным указанием записи его в координатной форме (12) и определением нормы отдельного вектора (14) приводит к появлению метрического пространства. Оно было названо евклидовым. Будем обозначать его через Е.

Норма вектора в евклидовом пространстве для n=2 и n=3 имеет ясный геометрический смысл. Она совпадает с длиной вектора и может быть выражена тем числом, которое мы получаем, приложив линейку к вектору.

Евклидово пространство в трехмерном случае совпадает с физическим пространством. Евклидовым линейное пространство названо по имени древнегреческого математика Евклида, создавшего в 3 в. до н. э. Евклидову геометрию – «первое приближение для описания структуры реального физического пространства» (БСЭ).

Введенный нами математический аппарат позволяет описывать евклидовы пространства раз­личных размерностей, рассматривая наше физическое пространство как частный случай и фило­софски осмысливая тот факт, что природа, создавая физический мир, остановилась на цифре три.

Свойства векторов в евклидовом пространстве.

1) Если вектор нулевой, т.е. , то его норма , и обратно: если , то вектор нулевой.

2) , где .

◄Действительно, .►

3) - неравенство Коши-Буняковского.

Неравенство Коши-Буняковского как свойство векторов метрического пространства с евклидовой нормой была доказано в §4.4 «Метрические пространства» для обоснования 3-ей аксиомы метрики. Доказательство проводилось в координатной форме для евклидовой нормы. Введение скалярного произведения позволяет провести доказательство в более компактной векторной форме.

◄Для доказательства введем параметр . По определению скалярного произведения неравенство

верно для любых векторов и . Преобразуем неравенство к квадратному относительно :

.

При неравенство верно. Следовательно, дискриминант квадратного трехчлена должен быть меньше либо равен нулю

.

Отсюда или . ►

Замечание. Из неравенства Коши - Буняковского следует .

4) - неравенство треугольника.

Третья аксиома метрики привела к необходимости доказывать неравенство треугольника, что и было сделано сведением его к неравенству Коши-Буняковского. Наличие скалярного произведения и здесь позволяет применить язык более высокого уровня.

◄С одной стороны, .

С другой стороны, .

Воспользуемся неравенством .

Тогда .

Значит, .

Извлечем квадратный корень и получим неравенство треугольника. ►

Определившись с длинами, перейдем к формулированию понятия угла в евклидовом пространстве.

Определение. Углом между ненулевыми векторами и евклидова пространства называ­ется число , определяемое из равенства

, где . (15)

Из замечания к свойству 3 введение угла таким образом (15) является корректным.

Два ненулевых вектора и называются ортогональными, если их скалярное произведение равно нулю, т. е. . Из равенства следует, что или угол . Для двух или трехмерного пространства ортогональность векторов означает, что они взаимно перпендикулярны.

Для ортогональных векторов в свойстве 4 неравенство заменяется равенством

,

которое называется теоремой Пифагора в евклидовом пространстве.

Ортонормированная система векторов

Система векторов называется ортогональной, если при , и нормированной, если для всех . Если векторы системы ортогональны и нормированы, они называются ортонормированными.

Замечание. Чтобы нормировать ненулевой вектор, необходимо разделить его на норму. Пусть задан вектор . Его норма . Нормированный вектор имеет вид , откуда .

(о независимости ортонормированной системы векторов)

Ортонормированная система векторов линейно независима.

◄Докажем, что ортогональные и нормированные векторы линейно независимы, т.е. докажем, что равенство

справедливо лишь при . Умножив обе части равенства скалярно на вектор , получим

или .

Отсюда следует . Умножая последовательно равенство скалярно на , будем иметь .►

(о существовании ортобазиса)

Во всяком -мерном евклидовом пространстве существует ортонормированный базис.

◄Доказательство теоремы представляет собой алгоритм последовательного построения ортонормированного базиса по заданному базису , названный методом ортогонализации или процедурой Грама-Шмидта.

Положим вектор и нормируем его: , получив первый вектор ортонор­миро­ванного базиса. Построим вектор

(16)

так, чтобы он был ортогонален вектору . Должно выполняться условие . Из этого условия найдем . Умножив скалярно равенство (16) на , получим

,

откуда . Тем самым вектор станет ортогональным вектору . Тогда вторым вектором ортонормированного базиса станет вектор .

Пользуясь найденными векторами , и заданным вектором , построим вектор

, (17)

ортогональный единичным векторам и , для чего умножим скалярно равенство (17) последовательно на и и приравняем нулю:

;

.

Поскольку , , получим , . Теперь вычислим вектор

.

Затем нормируем его, сделав третьим вектором ортонормированного базиса . Продолжая процесс ортогонализации, по заданному базису построим ортонормированный базис (или ортобазис) .►

На этом этапе вернемся к матрице Грама. Теперь ясно, что условие единичности матрицы (11) может быть выполнено. Ортонормированный базис удовлетворяет условиям (11). Значит, в ортонормированном базисе матрица Грама принимает вид единичной матрицы, и скалярное произведение оказывается равным (12).

Докажем свойство 4) матрицы Грама.

◄Пусть некоторый базис евклидова пространства размерности n, который может быть разложен по ортонормированному базису . Матрица перехода, столбцами которой являются координаты векторов в базисе , имеет вид

T= .

Тогда

.

Следовательно, .

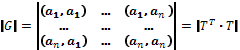Поскольку для любой матрицы справедливо , то . Если система векторов линейно зависима, то , и, следовательно, ►

ПРИМЕР. Методом ортогонализации построить ортонорми­рованный базис по базису евклидова пространства

Положим вектор и нормируем его: .

Построим вектор так, чтобы выполнялось условие . Получим

,

откуда .

Вычислим вектор : .

Нормируем вектор : .

Векторы и образуют ортонормированный базис евклидова пространства.

Проверка: , .

Ортогональное дополнение

П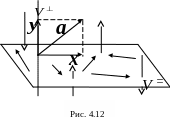 усть задано евклидово пространство . Пусть - некоторое линейное подпространство евклидова пространства .

Определение. Совокупность векторов пространства , обладающих свойством

, (18)

где - произвольный вектор из , называется ортогональным дополнением к подпространству . На рис. 4.12 изображено трехмерное евклидово простран­ство. В нем стрелками указаны векторы, из которых состоит ортогональное дополнение и которые ортогональны всем векторам из линейного подпространства . В изображении векторов мы отошли от соглашения об откладывании всех векторов от начала координат.

Свойства ортогонального дополнения

1. Ортогональное дополнение есть линейное подпространство евклидова пространства .

◄ Пусть векторы и принадлежат , вектор - произвольный вектор из . Тогда . Сложив скалярные произведения, получим

.

Следовательно, .

Если , то и , где , т.е. из следует .►

2. Линейное пространство есть прямая сумма подпространств и , т.е., с одной стороны, сумма и есть все пространство , с другой стороны, сумма и не содержит пересечения и .

◄ Пусть - ортонормированный базис : - ортонорми­ро­ван­ный базис . Среди системы векторов:

,

нет одинаковых. Действительно, если, например, векторы и совпадают, то , что противоречит условию .

Эта система ортонормирована, следовательно, линейно независима. Докажем, что она образует базис -мерного евклидова пространства. Предположим, что это не так, что число

.

Тогда существует вектор пространства, такой, что система векторов

, ,

линейно независима. Применим к этой системе процесс ортогонализации. Построенный на основе вектор будет ортогонален , значит . Совокупность векторов и ортонормирована. Следовательно, вектор увеличивает базис подпространства на единицу, что противоречит условию: - ортонорми­ро­ван­ный базис . Таким образом, система векторов , является базисом -мерного евклидова пространства, т.е.

.►

Из свойства 2 следует, что любой вектор пространства можно представить, причем единственным образом, в виде суммы векторов из и :

.

Вектор называется ортогональной проекцией вектора на линейное подпространство , а вектор - его ортогональной составляющей (рис. 4.12).

3. Минимальным расстоянием между вектором и линейным подпространством является длина его ортогональной составляющей на подпространство .

◄Рассмотрим евклидово пространство с метрикой и соответствующей нормой. Пусть вектор разложен на ортогональную проекцию и ортогональную составляющую к подпространству

, где , а .

Тогда квадрат расстояния между вектором и подпространством , составленном из множества векторов , _, можно найти из

Следовательно, и при . Таким образом, минимальным расстоянием между вектором и линейным подпространством является длина его ортогональной составляющей на это подпространство.►

Если задан вектор и известен ортонормированный базис подпространства , то могут быть найдены ортогональная проекция и ортогональная составляющая вектора . Разложим искомый вектор по базису с пока неизвестными коэффициентами разложения : .

Представим вектор в виде суммы ортогональной проекции и ортогональной составля­ющей : или .

Умножим обе части последнего равенства скалярно на вектор

,

откуда первый коэффициент разложения . Повторив действия с векторами , получим остальные коэффициенты ,…, . Следовательно, искомый вектор представляется как

, (19)

а вектор как .

Аналогично решается задача нахождения ортогональной проекции и ортогональной составляющей вектора при заданном векторе и известном ортонормированном базисе подпространства .

Замечание. Определение ортогональной проекции вектора на подпространство является частным случаем проектирования вектора на одно подпространство параллельно другому.

ПРИМЕР. Подпространство линейного 4-х-мерного пространства задано системой уравнений

Найти ортогональную проекцию вектора на подпространство и его ортогональную составляющую.

Решение. Найдем ортонормированный базис подпространства , для чего определим набор фундаментальных решений системы. Общее решение однородной системы:

, где .

Векторы и образуют фундаментальный набор решений и, следовательно, базис подпространства . Векторы ортогональны. Их нормы и . Поэтому ортонормированный базис подпространства :

, .

Найдем скалярные произведения :

, .

Ортогональная проекция вектора на подпространство (см. формулу (19))

.

Ортогональная составляющая

.

Проверка: .

Векторы и ортогональны.

Чаще встречается случай, когда в известен базис, не являющийся ортонормированным. В этом случае возможен процесс ортогонализации имеющегося базиса, но можно обойтись и без этой процедуры.

◄Пусть . (20)

Умножим скалярно равенство (20) на , затем его же на и т. д. Получим систему k уравнений c k переменными , которые таким образом можно найти. Разложив вектор x по базису , найдем вектор y.

ПРИМЕР. Продолжим решение предыдущей задачи. Умножим скалярно уравнение (20) на и . Получим систему

.

В численном виде

.

Ее решение . Тогда ). Затем находится вектор y.

Задача может быть решена в общем виде. Найдем формулу, использование которой сразу приводит к искомому результату.

◄Пусть задан базис подпространства в евклидовом пространстве :

,

……………………….

,

где координаты векторов даны в ортонормированном базисе, с матрицей перехода (в данном случае матрица перехода не является квадратной). Разложение вектора на ортогональную проекцию и ортогональную составляющую представим как

. (21)

Вектор запишем как матрицу , вектор как матрицу Тогда

, где

Умножим скалярно векторное равенство (21) последовательно на векторы , …, , учтем, что , , и составим систему уравнений

(22)

Левая часть системы (22), записанная в координатах,

,

,

……………………………………….,

в матричном виде выглядит так: . Правая часть системы (22) содержит матрицу Грама, поэтому в матричном виде записывается . Имеем матричную систему уравнений, в которой укажем размеры матриц

Следует учесть, что не существует обратной матрицы . Найдем матрицу-столбец X. Выразим из 2-го уравнения матрицу

и подставим в 1-е уравнение . ►

Матрица с размерами называется проектором из пространства на подпространство размерностью .

В частности, предыдущая задача решается простым преобразованием матриц

.

Откуда вектор , записанный в координатах в виде матрицы-строки, равен .

Линейные многообразия в евклидовом пространстве.

Пусть - есть линейное многообразие в евклидовом пространстве. Вектор , ортогональный к , называется нормальным вектором линейного многообразия.

Перечислим его свойства и укажем некоторые преобразования, в которых он участвует.

1. Любое линейное многообразие содержит нормальный вектор .

2. Существует только один нормальный вектор к линейному многообразию.

3. Среди всех векторов линейного многообразия нормальный вектор имеет наименьшую длину.

4. Любой вектор х линейного многообразия может быть разложен на ортогональную проекцию и ортогональную составляющую на направляющее подпространство V(x), причем ортогональная составляющая совпадает с нормальным вектором :

.

5. Расстояние между вектором и линейным многообразием равно модулю разности ортогональной составляющей этого вектора на направляющее подпространство и нормального вектора .

◄Расстояние между вектором и линейным многообразием в евклидовом пространстве есть

Множество векторов составляет . Поэтому

.►

6. Расстояние между двумя линейными многообразиями равно модулю разности нормальных векторов этих линейных многообразий.

◄Пусть даны линейные многообразия и с нормальными векторами и . Расстояние между и

.►

Кроме параллельности и скрещивания линейных многообразий в евклидовых пространствах вводится ортогональность двух линейных многообразий и , которая означает, что для любых двух векторов и скалярное произведение равно нулю:

, если и справедливо равенство .

ПРИМЕР. Найти расстояние между линейными многообразиями и

: :

Решение. Выделим в решении каждой системы ФНР и базисное решение

и

У чтем, что . Перейдем к ортобазису

и

где . Тогда линейные многообразия будут иметь вид

и .

Расстояние между ними

Сумма подпространств

Найдем ортогональную проекцию вектора на подпространство и его ортогональную составляющую .

Ортогональная проекция:

.

Ортогональная составляющая:

.

Расстояние между двумя линейными многообразиями есть длина ортогональной составляющей .

Задача имеет простую геометрическую интерпретацию. Линейные многообразия и представляют собой две параллельные прямые, одна из которых сдви­нута относительно другой на единицу вдоль оси (рис. 4.13). Направляющие подпространства и ли­не­­й­ных многообразий совпадают и описывают прямую, проходящую через начало координат с еди­ничным направляющим вектором . Поскольку ортогональная проекция вектора на подпростран­ство равна нулю, модуль вектора и будет расстоянием между линейными многообразиями и .

Заканчивая последнюю лекцию семестра, построим блочную структуру тех разделов линейной алгебры, которые были пройдены в течение семестра (рис. 4.14). Матричная алгебра и теория систем линейных уравнений позволили разработать математический аппарат для работы с векторами и векторными пространствами. Геометрические векторы, которые рассматривались еще в школе, алгебра векторных множеств, аналитическая геометрия познакомили с применением векторов при описании реального физического пространства. Затем была развита общая теория математического описания линейных векторных пространств и многообразий, введена метрика. Как частный случай векторных пространств с метрикой, были построены n-мерные евклидовы пространства. Одним из них является наше трехмерное физическое пространство.

Вопросы для повторения

1. Дать определение линейного пространства.

2. Дать определение векторного пространства.

3. Сформулировать определение размерности и базиса векторного пространства.

4. Как разложить произвольный вектор по базису?

5. В чем заключается идея дополнения линейно независимых векторов до базиса?

6. Как перейти от одного базиса векторного пространства к другому?

7. Что называется линейным подпространством векторного пространства?

8. Сформулировать определения суммы и пересечения линейных подпространств.

9. Что такое норма вектора?

10. Какие векторы составляют ортогональное дополнение?

11. Что называется линейным многообразием?

12. Как определяется метрическое пространство?

13. Какое векторное пространство называется евклидовым?

14. Как определяются длины и углы в евклидовом пространстве?

15. Какой базис называется ортонормированным?

16. В чем суть метода ортогонализации?

17. Что такое ортогональное дополнение?