Глава 3. Векторная алгебра
§ 3.1. Векторы на плоскости и в пространстве (геометрические векторы)
Линейные операции над векторами Координаты вектора Скалярное произведение векторов Свойства скалярного произведения Векторы в трехмерном пространстве |
Определение.
Вектором
на плоскости или в пространстве называется
направленный отрезок, имеющий начальную
и конечную точки. Обычно вектор
обозначается строчной буквой с чертой
либо буква выделяется жирным шрифтом
,
или же двумя заглавными буквами,
обозначающими начало и конец вектора
.
Мы будем векторы называть свободными,
если начальную точку можно выбирать
произвольно. Такие векторы можно
произвольно переносить параллельно
самим себе.
Определение.
Длиной
или модулем
вектора называется число, равное длине
направленного отрезка. Вектор, длина
которого равна единице, называется
единичным
вектором, или ортом.
Вектор, начало и конец которого совпадают,
называется нулевым
и обозначается
.
Векторы, лежащие на параллельных прямых,
называются коллинеарными.
Линейные операции над векторами
1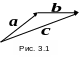
)
Суммой
векторов
и
называется вектор
,
начало которого совпадает с началом
вектора
,
а конец - с концом вектора
(рис. 3.1). Этот способ построения суммы
векторов называется правилом
треугольника.
Если на векторах и , как на сторонах, построить параллелограмм, то большая диагональ параллелограмма будет суммой векторов и . Этот способ построения суммы векторов называется правилом параллелограмма (Рис.3.1).
2)
Произведением
числа
на вектор
называется вектор
,
имеющий длину
.
Направление вектора
совпадает с направлением
,
если
,
и противоположно по направлению, если
.
3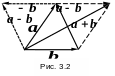
)
Разностью двух векторов
и
называется вектор
.
На рис. 3.2 вектор
изображен пунктиром. Сумма векторов
и
также изображена пунктиром. Легко
видеть, что
есть меньшая диагональ параллелограмма.
Укажем основные свойства линейных операций над векторами.
1)
;
2)
;
3)
;
4)
.
Координаты вектора
Зададим
на плоскости точку О
и назовем ее полюсом.
Отложим от точки О
как от начала два разнонаправленных
неколлинеарных вектора 
и проведем через полюс две прямые,
определяемые этими векторами. Полюс О
вместе с прямыми образуют на плоскости
так называемую аффинную
систему координат1,
в которой точка О
называется началом координат, а прямые
– осями координат. Они называются осью
абсцисс
и осью
ординат
и обозначаются как Ох
и Оу.
Используются обычно одинаковые масштабы
по осям, но они могут и различаться.
Аффинную систему координат с прямым
углом между осями называют как правило
декартовой
системой координат.
Сам Декарт употреблял только систему
координат на плоскости, но в дальнейшем
она была расширена на трехмерное
пространство добавлением оси
аппликат
(ось Oz),
перпендикулярной плоскости Oxy.
К
оординатами
вектора
в аффинной системе координат называются
координаты его конечной точки при
условии, что начальная точка вектора
лежит в начале координат. В дальнейшем
по умолчанию будем считать, что все
векторы отложены от начала координат.
На
рис. 3.3 изображена декартова (прямоугольная)
система координат, в которой координатами
вектора
на плоскости ХОУ
являются два числа
и
,
что обычно записывается в виде
.
Пусть вдоль осей Ох
и Оy
направлены векторы единичной длины i
и j.
Тогда произвольный вектор
может
быть представлен в виде суммы единичных
векторов i
и j
с коэффициентами
и
,
что соответствует правилу параллелограмма.
Если
вектор отложен от точки 
,
не совпадающей с началом координат
(свободный вектор), до точки 
,
то координатами вектора 
будем считать координаты 
Запишем
линейные операции над векторами в
координатах. Пусть заданы векторы
и
.
1)
;
2)
;
3)
.
П
роекция
вектора
Проекция
вектора 
на
направление, задаваемое вектором 
,
определяется формулой
,
где
α – угол между векторами
и
(рис. 3.4). Проекции 
на декартовы оси координат представляют
собой координаты вектора
,
умноженные на единичные векторы,
направленные вдоль осей
,
Косоугольные системы координат
При
изучении векторных пространств нам
придется иметь дело с аффинными системами
координат, у которых углы между осями
координат отличаются от 
.
Такие системы координат называются
косоугольными. Величины проекций 
вектора
на
косоугольные декартовы оси координат
будут зависеть от угла между осями.
Говорят, например, что 
есть проекция вектора
на
ось х
параллельно
оси y
(рис.
3.5). Построив векторы
как единичные вдоль осей Ox
и Oy,
получим разложение вектора 
по осям с коэффициентами 
.
По умолчанию в разделе геометрических векторов мы будем ориентироваться на прямоугольную декартову систему координат.
Скалярное произведение векторов
Определение.
Скалярным
произведением
двух векторов называется произведение
модулей этих векторов, умноженное на
косинус угла между векторами и обозначаемое
:
. (1)
Н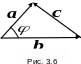
айдем
скалярное произведение, выраженное
через координаты векторов. На координатной
плоскости построим векторы
,
и
.
Они образуют треугольник, изображенный
на рис. 3.6. По теореме косинусов найдем
длину стороны, образуемой вектором
:
.
Отсюда
следует 
.
Выразим векторы через их координаты
,
,
.
Тогда
.
Раскроем скобки и приведем подобные. Получим
, (2)
т.е. скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Рассмотрим некоторые следствия формулы (2)
1)
В скалярном произведении положим
.
Тогда
,
т.е. скалярный квадрат вектора равен квадрату его длины.
2)
Найдем из равенства (1) величину
.
3)
Пусть вектор
направлен вдоль оси ОХ
и имеет единичную длину
,
т.е.
.
Тогда для всякого вектора
величина
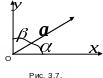
описывает
косинус угла между вектором
и положительным направлением оси ОХ.
Точно также при направлении единичного
вектора
вдоль оси ОУ
величина
описывает
косинус угла между вектором
и положительным направлением оси ОУ
(рис. 3.7).
и
называются
направляющими косинусами вектора
.
Свойства скалярного произведения
1)
;
Справедливость свойства вытекает из формулы (1), если учесть четность функции .
2)
.
Пусть
векторы
заданы своими координатами
,
,
.
Запишем скалярное произведение
в координатах:
.
Выражения,
представленные в скобках, есть
соответственно скалярные произведения
и
.
Отсюда следует свойство (2).
3)
.
Действительно,
,
,
При
имеем
,
.
Правые части трех равенств равны
.
При
имеем
,
,
,
т.е. опять получаем равенство правых
частей.
При
свойство 3 очевидно.
Векторы в трехмерном пространстве
Рассматривая векторы в трехмерном пространстве, переведем некоторые понятия, обсужденные ранее на элементарном уровне, в строгие определения .
В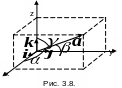
трехмерном пространстве вектор задается
тремя числами:
.
Линейные операции над векторами
и
в пространстве аналогичны операциям
над векторами на плоскости:
1)
;
2)
;
3)
.
4)
;
5)
6) Направляющие косинусы вектора
где
- углы между вектором
и положительными направлениями осей
ОХ,
ОУ, OZ
соответственно (рис. 3.8), причем
.
Замечание.
Пусть вектор
является единичным, т.е.
.
В этом случае
.
Следовательно, единичный вектор полностью
задается своими направляющими косинусами
.
Пусть
заданы векторы единичной
длины
,
направленные вдоль осей x,y,z
соответственно (рис. 3.8). Они обладают
следующими свойствами
1)
Заданные в координатах, они имеют вид:
.
2) Матрица, составленная из координат векторов
,
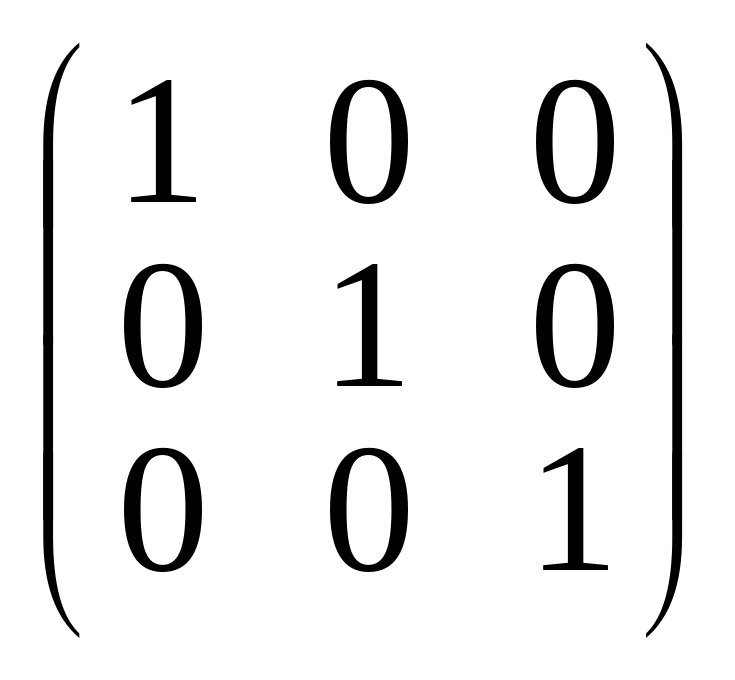имеет ранг, равный 3. Отсюда следует, что строки линейно независимы. На этом основании будем считать геометрические векторы линейно независимыми.
3) Векторы перпендикулярны друг к другу (взаимно ортогональны).
4)
Пусть задан произвольный вектор
.
Векторы
лежат на соответствующих координатных
осях, а их сумма по правилу параллелограмма
равна
. (3)
Тройка векторов, обладающих перечисленными свойствами, называется ортонормированным базисом (ортобазисом). Всякий вектор может быть разложен по ортонормированному базису. Формула (3) называется разложением вектора по векторам .
Замечание
1.
Если среди векторов базиса существует
хотя бы один вектор неединичной длины
или не ортогональный к какому-либо
вектору базиса, то скалярное произведение
,
записанное в координатах, будет иметь
другой вид.
Замечание 2. Излагая материал в §3.2 и §3.3, мы будем опираться на ортобазис по умолчанию. Начиная с §3.4, это соглашения снимается.
ПРИМЕР.
Найти скалярное произведение двух
векторов
и
.
Решение. Запишем скалярное произведение векторов и :
.
Пользуясь вторым свойством скалярного произведения, находим
Учитывая,
что 
=
=
,
,
Получаем
.