§ 3.3. Элементы аналитической геометрии

Уравнение прямой линии. Уравнение плоскости.

Рассмотрим задачи описания линейных математических объектов в трехмерном пространстве. Получим уравнения, которые описывают всю совокупность точек этих объектов, и которые не справедливы для всех остальных точек пространства. Весьма эффективным является векторный подход. Каждой точке трехмерного пространства ставится в соответствие вектор, начало которого совпадает с началом системы координат, а конец – с рассматриваемой точкой пространства. Тогда бесконечное множество точек пространства будет описано бесконечным множеством соответствующих им векторов, которое можно назвать векторным пространством. Будем рассматривать вектор как матрицу-строку или матрицу-столбец.

Уравнение прямой линии.

Положение прямой линии в пространстве будет определено, если задать точку , через которую проведена прямая, и ее направление в пространстве. Точка задается вектором , называемым вектором сдвига, направление - ненулевым вектором . Построим прямую параллельную вектору и проходящую через начало координат (рис. 3.13). Совокупность точек прямой задается уравнением

, (4)

где t – некоторая переменная, каждому значению которой соответствует определенная точка на прямой . Переменная t может принимать любые значения в зависимости от положения точки на прямой. Равенство (4) выполняется для любой точки прямой и нарушается, если точка оказывается вне прямой. Следовательно, равенство (4) выражает свойство, присущее исключительно точкам прямой и может быть названо векторным уравнением прямой При сдвиге множества точек прямой на вектор возникнет прямая, проходящая через точку . Ее векторное уравнение имеет вид

(5)

Пусть , , . Расположив координаты векторов по столбцам, получим

, где (6)

Уравнение (6) называется уравнением прямой в координатах. Запишем это равенство как три уравнения.

Выразим из каждого уравнения переменную t и приравняем дроби. Получим

(7)

Уравнение (7) называется каноническим уравнением прямой в координатах.

Уравнение прямой можно записать также системой линейных уравнений. Из раздела «Системы линейных уравнений» нам известно, что равенство (6) есть решение неоднородной системы из двух независимых уравнений с тремя переменными

. (8)

Чтобы раскрыть геометрическое содержание уравнений системы, рассмотрим задачу на составление уравнения плоскости.

Уравнение плоскости.

Плоскость в трехмерном пространстве можно определить двумя пересекающимися векторами , и точкой , через которую проведена плоскость.

Построим вспомогательную плоскость R на двух пересекающихся векторах , проходящую через начало координат. Любая точка N на плоскости может быть задана вектором . Разложим вектор по правилу параллелограмма по векторам и

. (9)

где – некоторые множители. Равенство (9) выполняется для любой точки плоскости и нарушается, если точка оказывается вне плоскости R. Следовательно, равенство (9) выражает свойство, присущее исключительно точкам плоскости и может быть названо векторным уравнением плоскости. Плоскость P, проходящую через точку , получим при сдвиге множества точек плоскости R на вектор . Векторное уравнение плоскости P имеет вид

(10)

Напишем уравнение в координатах

, (11)

где

Это равенство представляет решение неоднородного уравнения

(12)

и содержит фундаментальный набор решений однородного уравнения плюс частное (базисное) решение неоднородного уравнения.

Можно сделать вывод о том, что всякая плоскость в трехмерном пространстве определяется неоднородным уравнением первой степени относительно трех переменных. Верно и обратное утверждение: всякое уравнение первой степени относительно трех переменных описывает плоскость в трехмерном пространстве.

Становится понятным геометрическое содержание уравнений в системе (8), определяющей линию в пространстве. Каждое уравнение описывает плоскость. Их пересечение определяет прямую.

Для составления уравнения плоскости можно использовать вектор, перпендикулярный плоскости. Пусть плоскость проходит через точку , заданную вектором перпендикулярно вектору . Проведем вектор в произвольную точку М этой плоскости. Для вектора , лежащего в рассматриваемой плоскости, выполнено условие: . Поэтому скалярное произведение векторов равно нулю

.

В координатной форме

. (13)

Раскроем скобки и обозначим . Получим неоднородное уравнение первой степени относительно трех переменных, т.е. уравнение плоскости. Вектор называется в этом случае нормальным.

Замечание 1. Линейные математические объекты трехмерного пространства: прямую и плоскость – можно задать векторным уравнением или системой линейных уравнений (линейным уравнением).

Замечание 2. Если прямая или плоскость проходят через начало координат, векторные уравнения не будут содержать вектора , а линейные уравнения окажутся однородными.

Рассмотрим основные теоретические задачи аналитической геометрии, связанные с прямыми и плоскостями.

1. Уравнение прямой в векторной форме записать в виде системы линейных уравнений.

Представив векторное уравнение прямой (2) в координатах

уберем параметр t. Для этого выразим t из последнего уравнения и подставим в первые два.

После преобразований получим неоднородную систему из двух независимых линейных уравнений с тремя переменными

Она может быть записана в виде определителей

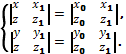
2. Уравнение прямой в виде системы линейных уравнений представить в векторной форме.

Эта задача рассматривалась при изучении систем линейных уравнений. Решение такой системы есть линейная комбинация фундаментального решения однородной системы уравнений плюс частное (базисное) решение неоднородной системы (6).

3. Уравнение плоскости в векторной форме записать в виде системы линейных уравнений.

Векторное уравнение плоскости (10) в координатной форме представим в виде системы из трех линейных уравнений с тремя переменными

В системе следует избавиться от параметров и . С этой целью рассмотрим вместе два последних уравнения как систему с двумя переменными и . Используя правило Крамера, получим

где .

Подставим полученные значения переменных и в первое уравнение системы

.

Раскроем определители, соберем слагаемые, содержащие , а также слагаемые с

.

Слагаемые в числителях запишем в виде определителей, умножим обе части равенства на и перенесем все в одну часть, получим

. (14)

Уравнение (14) есть уравнение плоскости. Величины определителей играют роль координат вектора перпендикулярного плоскости (см. уравнение (13)).

Свернем левую часть уравнения (14) до определителя 3-го порядка

.

Мы получили уравнение плоскости в виде линейного неоднородного уравнения с тремя переменными, записанного в компактной форме.

4. Уравнение плоскости в виде линейного уравнения представить в векторной форме.

Эта задача также рассматривалась при изучении систем линейных уравнений. Решение есть линейная комбинация фундаментального набора решений плюс частное (базисное) решение неоднородной системы (11).

5. Угол между прямой и плоскостью.

У равнение прямой возьмем в векторной форме (5), уравнение плоскости – в виде однородного линейного уравнения (13). Оба уравнения содержат координаты векторов: уравнение прямой – направляющий вектор , уравнение плоскости – перпендикулярный к плоскости вектор . Их скалярное произведение позволяет найти косинус угла между ними, на основе которого легко построить угол между прямой и плоскостью.

.

Спроектируем отрезок прямой с направляющим вектором на плоскость (рис. 3.15) и найдем угол между наклонной и ее проекцией на плоскость. Если угол острый, то , если угол тупой, то . Тогда .

6. Угол между плоскостями.

Для вычисления угла между плоскостями удобно воспользоваться уравнением плоскости как неоднородным уравнением первой степени относи­тельно трех переменных. Угол между плоскостями

и

равен острому углу между нормальными векторами к этим плоскостям. Если угол между векторами окажется тупым (косинус угла отрицателен), следует взять знак минус. Координаты нормальных векторов и равны коэффициентам перед переменными: , . Используя формулу скалярного произведения в координатах, получим

.

7. Расстояние от точки до плоскости.

Пусть заданы точка и плоскость P (рис. 3.16), заданная уравнением

.

Проекция вектора на направление, задаваемое перпендикулярным плоскости P вектором с учетом знака равна

.

Проекция вектора на это же направление равна

.

Расстояние от точки до плоскости P есть длина отрезка , равная

.

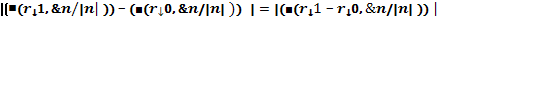В координатах расстояние от точки до плоскости определяется формулой

.

8. Расстояние между скрещивающимися прямыми.

Уравнения скрещивающихся прямых представим в векторной форме

- 1 прямая

- 2 прямая

Здесь и - направляющие векторы прямых, и - векторы сдвига (рис. 3.17). Перенесем вторую прямую в пространстве до пересечения с первой прямой, а первую прямую - до пересечения со второй. На двух пересекающихся прямых построим плоскости P и R. Пусть – вектор, перпендикулярный к плоскостям P и R. Его легко получить, как одно из решений системы

Рассуждая аналогично предыдущей задаче, получим проекцию вектора с учетом знака на направление, задаваемое вектором , в виде скалярного произведения

.

Тогда расстояние между скрещивающимися прямыми есть

.

§ 3.4. N-мерные векторы

Понятие n-мерного вектора Линейная зависимость и независимость векторов Свойства линейной зависимости и независимости векторов

Обобщим понятие вектора.

Понятие n-мерного вектора

Определение. n-мерным вектором называется математический объект, который состоит из упорядоченной совокупности действительных чисел, называемых координатами вектора и записываемый в виде . Название « -мерный вектор» связано с тем, что при или совокупность чисел можно интерпретировать как совокупность координат вектора на плоскости или в пространстве.

Замечание. Числа отсчитываются от начальной точки отсчета, принятой за нуль. Для геометрических векторов это означает, что начала векторов совпадают с началом координат.

Два -мерных вектора и называются равными, если равны все компоненты векторов, т.е. где .

Вводя правила сложения и умножения для n-мерных векторов, мы должны уточнить, как следует производить эти действия над совокупностями n действительных чисел. Иначе говоря, введем операции над -мерными векторами.

Суммой двух векторов и назовем вектор такой, что .

Произведением действительного числа на вектор назовем вектор такой, что .

Замечание. Введенные по определению операции над -мерными векторами аналогичны операциям над прямо­угольными матрицами. Поэтому n-мерные векторы можно рассматривать, как матрицы-строки или как матрицы-столбцы 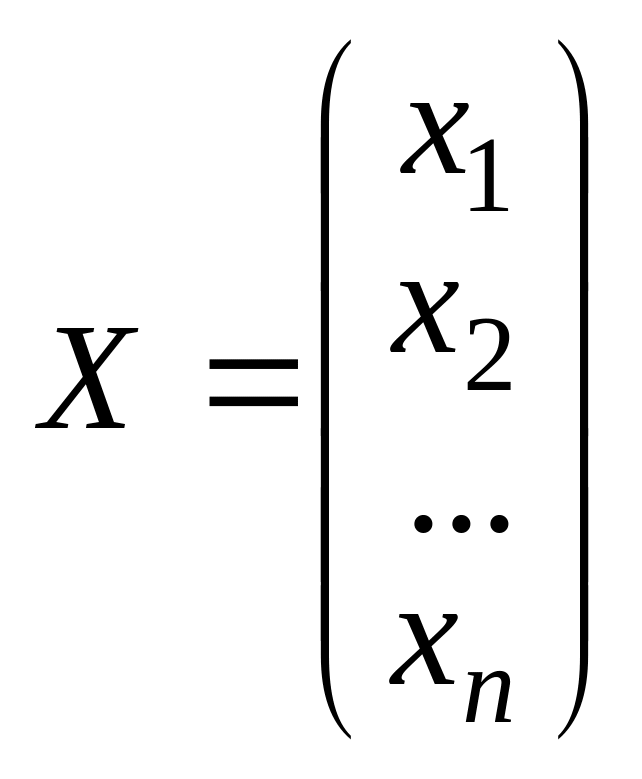и совершать над векто­рами матричные операции.

Линейная зависимость и независимость векторов

Пусть каждый из векторов в наборе есть n-мерный вектор.

Определение. Вектор называется линейной комбинацией векторов , если найдутся такие действительные числа , что

.

Векторы называются линейно зависимыми, если существуют такие числа , не все одновременно равные нулю, что

. (15)

Если равенство (15) выполняется только при , то векторы называются линейно независимыми.

ПРИМЕР. Даны два неколлинеарных вектора. Доказать, что они линейно независимы.

Решение. Предположим иное: векторы линейно зависимы. Тогда существуют не равные одно­вре­менно нулю числа , такие, что . Пусть для определенности . Разделив обе час­ти равенства на , получаем . Значит, векторы коллинеарны, что противоречит условию.

Свойства линейной зависимости и независимости векторов

1) Если среди нескольких векторов (набора векторов) один из них есть линейная комбинация части остальных, то весь набор векторов линейно зависим.

Пусть имеются векторы , причем вектор , где . Перенесем все члены в одну часть и дополним слагаемыми . Получим линейную комбинацию,

,

в которой нашлись , не все одновременно равные нулю. Значит, векторы линейно зависимы.

2) Если среди набора векторов имеется нулевой вектор, то весь набор векторов линейно зависим.

Пусть, например, нулевым является вектор . Тогда равенство (4) останется справедливым при , .

3) Если векторы линейно независимы и существует вектор , являющийся линейной комбинацией векторов , т.е. , то коэффициенты определяются по вектору единственным образом.

Пусть вектор можно представить как две линейные комбинации с различными коэффициентами и .

Тогда ,

откуда .

Из линейной независимости векторов вытекает, что

и, значит, .

ПРИМЕР. Являются ли векторы линейно зависимыми? Если да, найти всю совокупность значений коэффициентов, реализующих линейную зависимость.

Решение. Составим векторное равенство . Запишем его в матричном виде, представив векторы как матрицы-столбцы:

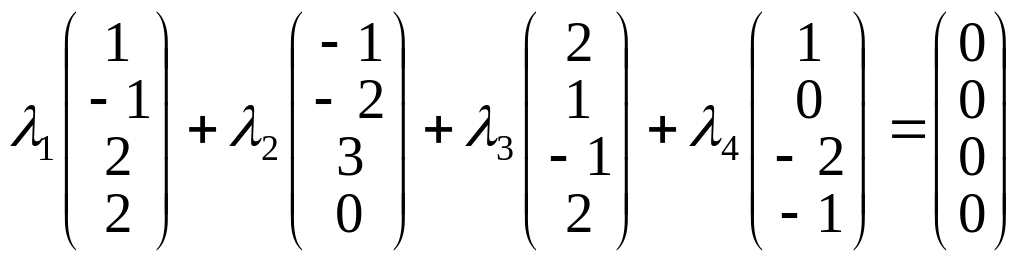. (16)

Равенство (16) есть система линейных однородных уравнений с четырьмя переменными. Составим матрицу из коэффициентов и определим ее ранг:

~ .

Очевидно, ранг матрицы равен 3. Система (5) имеет кроме нулевого решения , бесконечное множество решений. Следовательно, векторы линейно зависимы. Далее найдем структуру бесконечного множества решений, для чего продолжим элементарные преобразования со строками матрицы по методу Гаусса - Жордана:

.

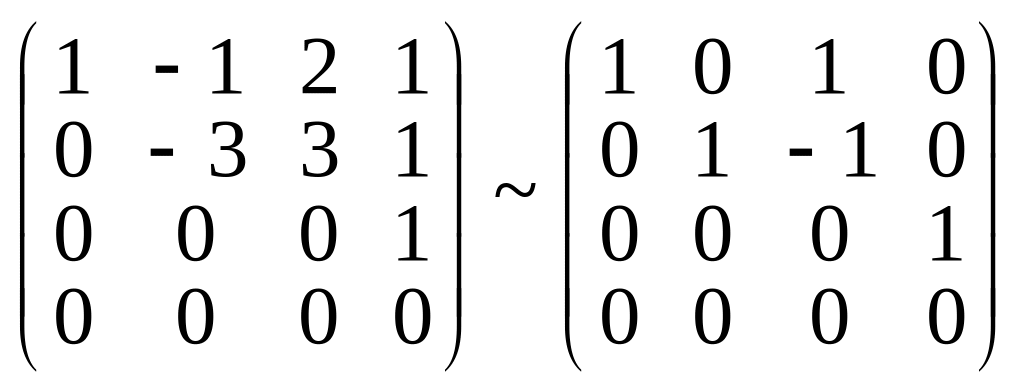Отсюда следует 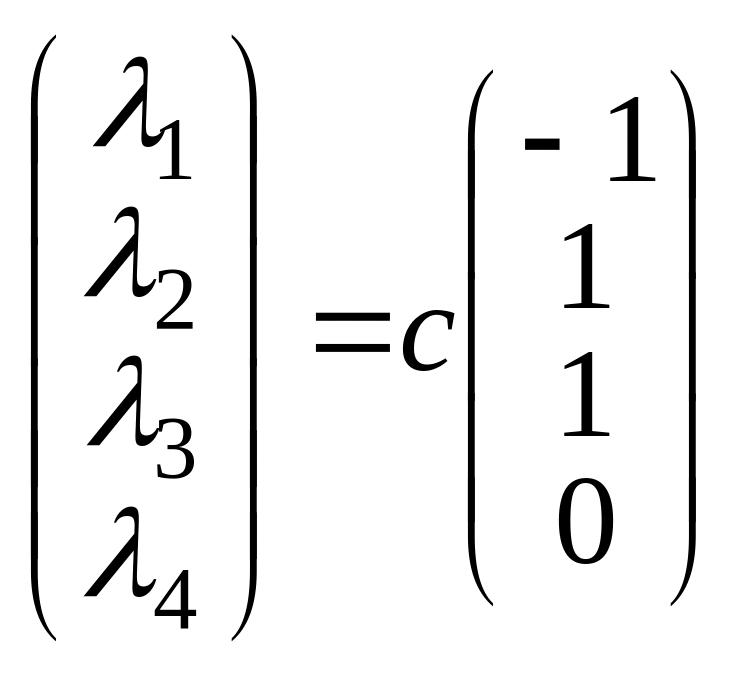, где . (17)

Решение (17) представляет всю совокупность значений коэффициентов , реализующих линейную зависимость векторов . Например, при имеем . Среди векторов три являются линейно независимыми, один – линейной комбинацией остальных. Линейно независимыми можно взять тройки векторов или, , или , но нельзя взять , поскольку в этом случае вектор невозможно через них выразить.

Замечание. Как видно из примера, вопрос о линейной зависимости векторов сводится к исследованию существования ненулевого решения у линейной однородной системы уравнений.

Вопросы для повторения

1. Сформулировать определение геометрического вектора и привести линейные операции над векторами.

2. Что такое аффинная система координат?

3. Что называется проекцией вектора на направление?

4. Определить скалярное произведение векторов и перечислить свойства скалярного произведения.

5. Какой базис называется ортонормированным?

6. Сформулировать определение суммы множеств векторов по Минковскому.

7. Ч то такое -мерный вектор? Привести операции над -мерными векторами.

8. Какие векторы называются линейно зависимыми?

9. Перечислить свойства линейной зависимости и независимости векторов.

1 Система координат названа аффинной от латинского слова affinis, что значит родственная. Термин обусловлен геометрическими преобразованиями фигур, при которых прямые переходят в прямые.

*Герман Минковский (1864-1909) –немецкий математик и физик, профессор Геттингенского университета.