§ 3.2. Алгебра векторных множеств

Сумма множеств в смысле Минковского Алгебраические операции над векторными множествами Сложение множеств (двумерный случай)

Сумма множеств в смысле Минковского^

_Пусть заданы два произвольных множества векторов. Векторы составляют множество А, векторы - множество В. Все векторы отсчитываются от начала координат. Определим сумму множеств по Минковскому следующим образом.

Сумма множеств есть совокупность различных векторов, каждый из которых составлен из двух векторов: один взят из множества А, другой из множества В, т. е.

, где или =

Это означает, что к каждому из векторов множества А прибавляется каждый из векторов множества В. В общем виде сумму будем записывать кратко в виде

ПРИМЕР 1. Если каждое из множеств составлено из двух векторов , , то сумма множеств по Минковскому содержит 4 вектора:

ПРИМЕР 2. Сумма двух одинаковых множеств и содержит 3 различных вектора:

.

Очевидно отличие от школьной алгебры чисел (a – число), алгебры матриц (А – матрица), булевой алгебры (А – булева переменная).

Алгебраические операции над векторными множествами

Введем свойства алгебраических операций над векторными множествами. Они вытекают из арифметических операций над векторами.

1. = .

2. , где .

3. Если нулевой вектор , то множество будет содержать множество В; если нулевой вектор , то множество будет содержать множество А.

◄Действительно, пусть среди векторов содержится нулевой вектор : . Тогда

.

Следовательно, среди векторов множества содержится множество векторов , т.е. .►

Аналогично доказывается второе утверждение свойства 3.

4. Множество есть параллельный перенос множества на вектор : .

5. Сумма множеств по Минковскому и может быть найдена следующим образом:

(находится сумма множеств по Минковскому, которая сдвигается на вектор ).

◄Доказательство очевидно. Следует вспомнить, что сумму четырех векторов можно сложить так: .►

Сложение множеств (двумерный случай)

Р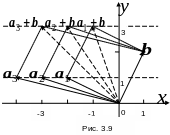 ассмотрим частный случай суммы Минковского, когда все векторы лежат на плоскости ХОУ, т.е. имеют по две координаты. Сумма множеств по Минковскому в этом случае получает наглядное геометрическое представление.

ПРИМЕР 3. Найти алгебраическую сумму по Минковскому двух множеств: и .

Решение. Множество В содержит один вектор. Следовательно, в соответствии со свойством 4 мно­жество А следует сдвинуть на вектор . Множество

е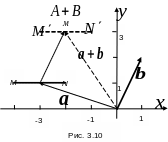 сть совокупность трех сумм векторов. Результат представлен на рис. 3.9. Векторы показаны пунктирными стрелками. Обратите внимание, что концы векторов , располо­женные на линии при сложении с вектором , были перенесены на линию .

ПРИМЕР 4. Найти алгебраическую сумму по Минковскому бесконечного множества векторов и множества .

Р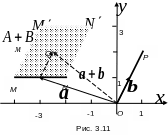 ешение. Запись означает, что концы векторов имеют координаты : . Множество А сдвигается на вектор . При сложении векторов, концы которых находятся на линии , с вектором , получаются векто­ры, концы которых находятся на линии . Геометрически это означает, что отрезок MN парал­лельным переносом переходит в отрезок (рис.3.10).

ПРИМЕР 5. Найти алгебраическую сумму по Минковскому бесконечного множества векторов и бесконечного множества векторов , .

Р ешение. При сложении одного из векторов , оканчивающегося на отрезке ОР (рис. 3.11), с одним из векторов множества А получается вектор с концом в точке Q. Складывая векторы с концами на отрезке MN c векторами, концы которых расположены на отрезке ОР, получим множество векторов, оканчивающихся на фигуре . Значит, фигура вместе со своими граничными точками и есть множество .

Замечание. Множество графически поставленных точек, из которых состоит фигура , можно считать концами векторов, начала которых находятся в начале координат.

ПРИМЕР 6. Найти алгебраическую сумму по Минковскому бесконечного множества векторов , где , и бесконечного множества векторов , где

Решение. Первое множество векторов оканчивается в круге радиусом 1 с центром в начале координат и показано прямоугольной штриховкой, второе множество векторов находится на отрезке ОР. Их сумма по Минковскому указана на рис. 3.12 множеством точек, которые можно представить как концы векторов.